Szilassi Lajos:

Egy átdarabolási feladat és története

Fermat szülőházában (ahol a nagy francia matematikus születésének 400. évfordulójával kapcsolatos ünnepségsorozat egyikén vehettem részt) megemlítettem, hogy a magyar matematikusok is készülnek egy nagy ünnepre, Bolyai János születésének 200. évfordulójára. A Bolyai név hallatán egyik vendéglátóm, Francois Padilla a decazeville-i középiskola matematikatanára azonnal elém tett négy kis fémlapból álló puzzle-készletet, amelyből ki lehetett rakni egy négyzetet, vagy egy szabályos háromszöget. (Később, nagy örömömre meg az iskola tanárai meg is ajándékoztak ezzel a "játékkal".) Többen bizonygatták, hogy ez Bolyai János konstrukciója, bár szerintem inkább Bolyai Farkasé lehetett. Mindenesetre én arra voltam büszke, hogy a Bolyai név ismerősen cseng egy - vasas szakmunkásokat képző - francia középiskolában, ők arra, hogy ezt a készletet az iskola egy olyan lézerrel működő gépével készítették, amely 0,01 mm pontossággal szabja darabokra a rozsdamentes krómacél lemezt. Bármelyik iskola joggal lehet(ne) büszke arra, hogy ilyen feladatok megoldására (is) használják azt a gépet.

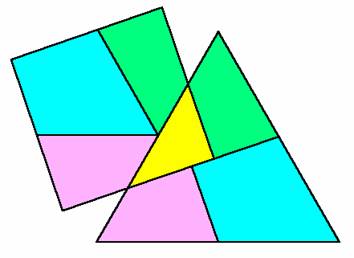
Bolyai Farkas vezette be a "végszerűen egyenlő" síkidomok fogalmát. Két síkidomot végszerűen egyenlőnek nevezett, ha az egyiket véges sok darabra szétvágva a kapott darabokból összeállítható a másik, vagyis ha a két síkidom véges számú, páronként egybevágó darabra osztható. Gondoljuk meg: a síkidomok közötti "végszerűen egyenlő" reláció sokkal szigorúbb, mint az, hogy két síkidom "egyenlő területű".

Bolyai Farkas nevéhez fűződik az a tétel, miszerint az egymással egyenlő területű sokszögek végszerűen is egyenlők.

E tétel egyik jelentős segédtételének tekinthető az alábbi állítás, melynek a pontos bizonyítását olvasóinkra bízzuk.

Egy hegyesszögű háromszöget daraboljuk át egy vele egyenlő területű négyzetté.

Legyen az ABC (hegyesszögű) háromszög AB oldalának a felezőpontja F₁, BC oldalának a felezőpontja F₂ . Legyen D az AC oldalnak az a pontja, melyre igaz, hogy DF₂ a keresett négyzet oldalának a hossza, (pl. valamelyik oldalának, valamint az ehhez tartozó magasság felének a mértani közepe.)

Legyen az A pont D-re vonatkozó centrális tükörképe M, az MC szakasz felezőpontja E . Legyen az F₁ pontnak az F₂D szakaszra eső merőleges vetülete T₁, az E pont ugyancsak F₂D-re eső merőleges vetülete T₂ .

Daraboljuk fel az ABC háromszöget a DF₂, F₁T₁ és ET₂ szakaszok mentén.

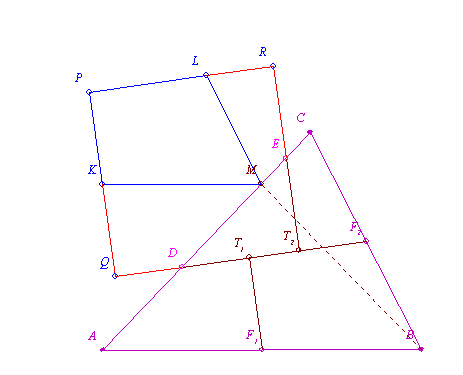
Azt állítjuk, hogy az így kapott síkidomok átrendezhetők a PQT₂R négyzetté, amelyben a PKML négyszög a T₁F₁BF₂ négyszögnek a BM vektorral eltolt képe, a KQDM négyszög az ADF₁T₁ négyszögnek a D-re vonatkozó centrális tükörképe, az ERLM négyszög pedig az ET₂F₂C négyszögnek az E-re vonatkozó centrális tükörképe.

Azt kell tehát belátni olvasóinknak, hogy ezekkel az egybevágósági transzformációkkal valóban egy négyzetet állítottunk össze a háromszög darabjaiból.

Nehezebb kérdés annak a belátása, hogy egy hegyesszögű háromszöghöz mindig megtalálható az az F₂D szakasz, amelynek hossza a háromszöggel egyenlő területű négyzet oldala, és erre teljesül, hogy azaz AM<AC, továbbá az F₁ és E pontoknak az F₂D egyenesre eső merőleges vetületei az F₂D szakasz belső pontjai lesznek.

További kérdés, hogy szükséges-e az a kikötés, hogy az ABC háromszög hegyesszögű legyen. Milyen háromszögekre teljesül a fenti feltétel?

Itt jegyezzük meg, hogy ezzel az eljárással átdarabolható a háromszög egy olyan téglalappá is, amelynek egyik oldala egy a fenti feltételeket kielégítő tetszőlegesen választott F₂D szakasz.

Ennek a tételnek az igazolásával mennyire jutottunk közel a Bolyai-tétel bizonyításához?

Végül vizsgáljuk meg - a vicc kedvéért - az alábbi kérdést: Igaz-e, hogy ha az ABC háromszög szabályos, akkor ,vagyis M az AC oldal felezőpontja? A rajz alapján úgy tűnik, igaz. Ha nem, "mennyire" nem?