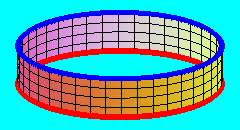
Induljunk ki egy nagyon egyszerű felületből, egy henger-palástból.

Ha ezt a felületet most topológiai szempontból vizsgáljuk, el kell tekintenünk a méretétől szélességétől, attól is, hogy a keresztmetszete kör. Bárhogyan nyújthatjuk, deformálhatjuk. Topológiai tulajdonságai, hogy ti. két határvonala van, vagy, hogy egyik oldala befesthető kékre, a másik pirosra, ettől nem változik.

A topológia alapművelete a folytonos deformálás. Így pl. a topológia nem tesz különbséget a hengerpalást, valamint az ebből folytonos deformálással kapható alakzatok között.

Fogalmazzunk kissé pontosabban: topológiai transzformációnak nevezzük egy ponthalmaznak egy másik ponthalmazba történő leképezését, ha az folytonos - azaz egymáshoz kellően közeli pontok képei is egymáshoz tetszőlegesen közel kerülnek - , létezik az inverze - azaz különböző pontok képei is különbözők lesznek - és a leképezés inverze is folytonos.

Két geometriai alakzat topológiailag ekvivalens - azaz homeomorf - ha topológiai transzformációval egyik a másikba átvihető.

A homeomorf transzformációk alkalmazása közben előfordulhat, hogy a felület metszi saját magát. Az, hogy van-e ilyen önátmetszés a felületen, nem tartozik a konstrukció topológiai tulajdonságai közé. Az önátmetszés helyét alkotó pontokat nem úgy kell tekintenünk, mint két felületdarab közös pontjait, hanem úgy, mint fizikailag egy helyen lévő, de egymástól különböző, sőt egymással nem is szomszédos pontokat.)

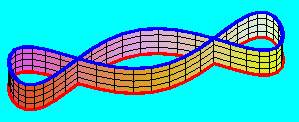
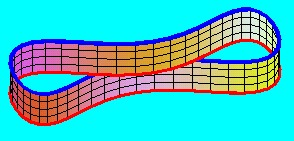
Azt mondhatjuk, hogy egy topológiai transzformációnak alávetett geometriai alakzatot - jelen esetben felületet - kényünk-kedvünk szerint deformálhatunk, csak nem szabad sehol elvágnunk, sem összeragasztanunk. Pontosabban: elvághatjuk ugyan, csak a megfelelő deformálás után ugyanott, ugyanúgy össze is kell ragasztanunk. Például megtehetjük egy henger palásttal, hogy elvágjuk, csavarunk rajta egy teljes fordulatnyit(360 foknyit), majd ugyanott, ugyanúgy összeragasztjuk. Ezzel ismét egymás közelébe kerülnek azok a pontok, amelyek eredetileg is egymás közelében voltak.

Ha tehát egy téglalap alakú szalagot a szemközti élei mentén összeragasztunk, topológiai szempontból henger-palástot kapunk akkor is, az összeragasztás előtt - esetleg többször is - teljes fordulattal megcsavarjuk.

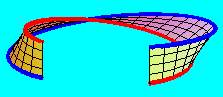Vegyünk most egy hosszú, keskeny papírcsíkot, tekerjünk rajta egy fél-fordulatnyit (180 foknyit),  majd ragasszuk össze a két végét. (Ha - megkülönböztetésül - a szalag egyik széle piros, a másik kék, akkor a piros szélét a kékhez kell illesztenünk.)

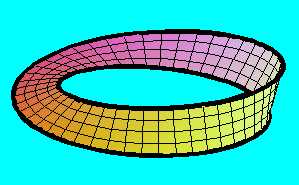
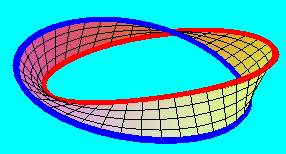
A keletkezett alakzat az un. Möbius-szalag, amelynek - mint látni fogjuk - sok érdekes tulajdonsága van. Legfontosabb, hogy ez egy un. egyoldalú, másképpen szólva nem irányítható felület, melynek egyetlen - körvonallal homeomorf - határvonala van. Az, hogy egyoldalú, azt jelenti, hogy nem tudnánk befesteni úgy, mint mondjuk egy körlapot, vagy henger palástot, egyik oldalról pirosra, a másikról kékre. Képzeljük el, hogy az elkezdjük a szalag festését egy helyen, gondosan ügyelve, hogy az ecsetünk többé-kevésbé merőlegesen álljon a felületre, és a szalag közepén haladjunk. Egyszerre csak azt tapasztaljuk, hogy visszatértünk a kiindulási pontba, csak most az ecset a kiindulási helyzetéhez képest pontosan az ellenkező irányban áll, miközben nem mentünk ki a szélére. Ráadásul a festéssel még csak félig vagyunk készen. Még egyszer végig kell mennünk a szalagon ahhoz, hogy az egész be legyen festve, és az ecset is úgy álljon, mint a festés kezdetekor.

Másképpen is származtatható a Möbius szalag:

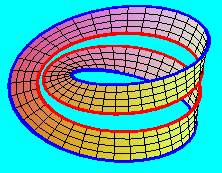
A kétszer csavart hengerpalást deformálható úgy, hogy az egyik határvonala önmagával összeragasztható legyen. Ha ezt az összeragasztást megtesszük, (amely természetesen nem topológiai transzformáció), akkor egy Möbius-szalagot kapunk. Ugyanezt úgy is megfogalmazhatjuk, hogy egy Möbius-szalagot a középvonala mentén elvágva egy kétszer csavart, hengerpalásttal homeomorf - tehát kétoldalú - felület keletkezik.

A Klein kancsó kissé bonyolultabb felület, könnyebb a származtatását inkább gondolatkísérletként elvégeznünk, mint előállítanunk a - kézbe vehető - modelljét.

Mint láttuk, a topológia nem tesz különbséget egy henger palást és az itt látható, változó keresztmetszetű, hajlított cső között, de megkülönbözteti a Möbius-szalagtól.

 

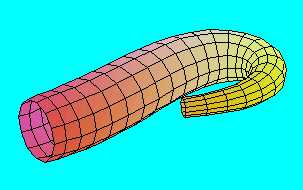
Topológiai szempontból nézve még akkor is csak egy henger palásttal van dolgunk, ha ezt a csövet átdugjuk saját magán. Ezzel a felület ugyan önátmetszővé válik, de említettük, hogy ez nem tartozik a topológiai tulajdonságai közé.

 

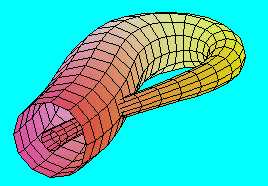
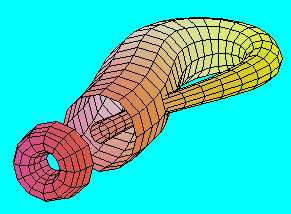
Ragasszuk most össze a hengerpalást két végét. Ezzel egy zárt, egyoldalú felülethez, a Klein-kancsóhoz jutunk.

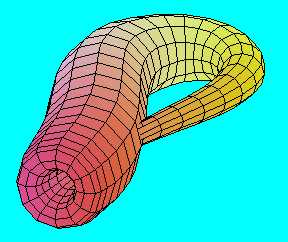
Alaposabban szemügyre vehetjük a konstrukciót egy "rácsos" modellen, amely lehetővé teszi, hogy kissé átlássunk a felületén.

Természetesen ettől kissé eltérő formájú Klein-kancsót is kaphatunk, ugyanígy származtatva a felületet.

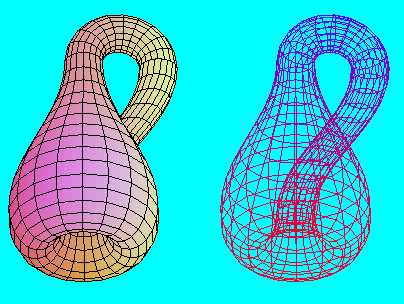
Ehhez persze folytonos deformálással - amely topológiai értelemben nem számít változtatásnak - néhány átalakítást végre kell rajta hajtanunk a felületen.

Lapítsuk le kissé,  majd hajlítsuk meg úgy, hogy a szalag keresztmetszete félkör legyen!

Változtassunk néhol a keletkező "vályú" szélességén, majd deformáljuk tovább úgy, hogy a határvonala egy síkra illeszkedjék.

Ez az utóbbi művelet csak úgy hajtható végre, hogy eközben önátmetszővé válik a felület, de mint említettük, ez nem topológiai tulajdonság, így még mindíg egy egyszerű Möbius-szalaggal van dolgunk.

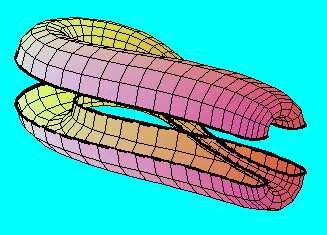
Az eddigi deformálások viszont alkalmassá tették a Möbius-szalagot arra, hogy összeragasszuk egy vele egybevágó másik Möbius-szalaggal, amelyet ebből egy síkra vonatkozó tükrözéssel kapunk.

Ezzel - elfeledve az összeragasztás határvonalát - valóban egy Klein-kancsóhoz jutottunk.

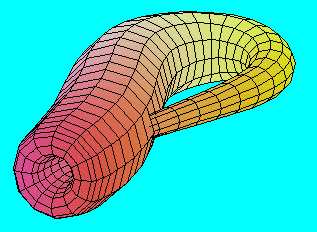
Térjünk most vissza a megszokott Möbius-szalaghoz, amelyet úgy kaptunk, hogy egy - szakasz keresztmetszetű - szalagot fél-fordulattal megcsavarva ragasztottunk össze!

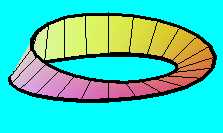
Ha e helyett egy félkör keresztmetszetű szalaggal végezzük el a fél-fordulatnyi csavarást (amely lényegében egy hengerpalást egyik fele), akkor a két végét egyenes szakasszá kell lapítanunk ahhoz, hogy simán össze tudjuk ragasztani a másik végével.

 

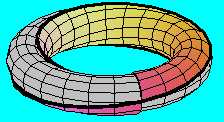
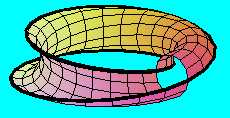
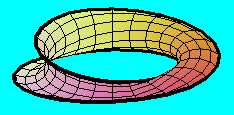
A "síma" Möbius-szalagot ellenkező irányba hajlítjuk félkör keresztmetszetűvé,amit a végein ugyanúgy belapítunk, akkor egy másik Möbius-szalagot kapunk, amelynek a határvonala ugyanaz, mint az előzőé, igy a két szalag máris össszeragasztható egyetlen - zárt - felületté,

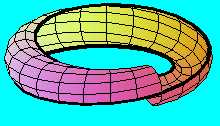
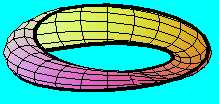
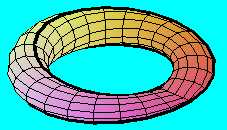
amely természetesen ugyancsak Klein-kancsó.

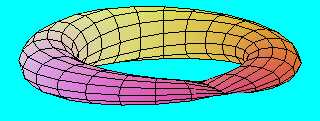
Ezzel az eljárssal egy olyan Klein-kancsót kapunk, amelyben az önátmetszés vonala - ami nélkül nem állítható elő zárt (azaz határvonal nélküli) egyoldalú felület - egyetlen szakasz.

Ha kezünkbe veszünk egy kétszer csavart hengerpalástot, tapasztalhatjuk, hogy "nyolcas" alakúvá deformálható, esetleg az önátmetszést is megengedve:

 

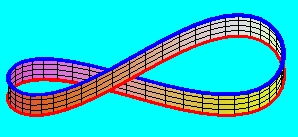
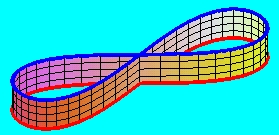
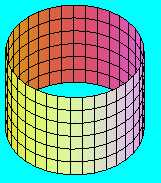
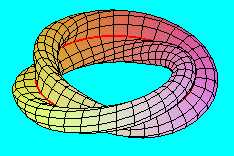
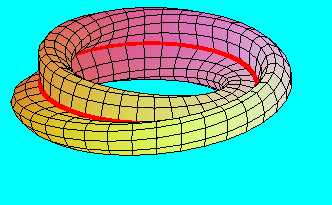
Ha ezeket a felületeket a határvonalaik mentén csavarás nélkül, vagy egy teljes fordulatú (360 fokos) csavarást követően ragasztjuk össze, egymással homeomorf tórusz felülethez jutunk, amely természetesen kétoldalú, azaz irányítható felület. (A piros vonallal itt az önátmetszés vonalát jelöltük.)

 

 

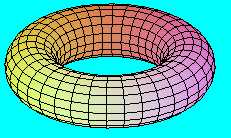
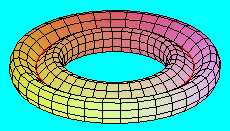
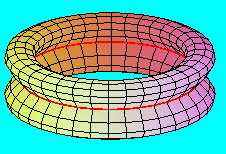
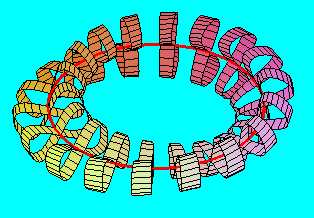
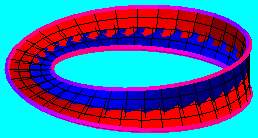
Ha azonban a "nyolcas keresztmetszetű" hengerpaláston egy félfordulatnyi csavarás után ragasztjuk össze a két - nyolcas alakú - határvonalat, akkor egy egyoldalú felületet kapunk, amely ugyancsak a Klein-kancsó. (Itt a pirossal jelölt önátmetsző vonal egyben a félfordulatnyi csavarás tengelye.) A szemléletesség kedvéért bemutatjuk a felületnek egy "szeletelt" változatát is.

Mint láttuk, a Möbius-szalag egyoldalú felület, nem tudjuk úgy befesteni, mint mondjuk egy körlapot, egyik oldalát pl. pirosra, a másikat kékre. Befesthetjük azonban úgy, hogy a határvonala egyik oldalán határozottan piros, a másikon határozottan kék legyen, ahol a két szín valahol a szalag középvonala táján fokozatosan átmegy egymásba.

Képzeljük most el, hogy van egy kiváló matematikai érzékkel rendelkező, de igen rövidlátó (csoda)bogár, amely ott áll az így befestett Möbius-szalag határvonalán. Azt látja, hogy a felület, amelynek a peremén áll, egyik oldala kék, a másik piros. Ha most elindul a felület peremén, egyszer csak visszaér a kiindulási helyére, miközben folyton azt tapasztalja, hogy a felület mindkét oldala ugyanolyan színű marad. Joggal hiheti, hogy egy olyan körlap peremén ballagott körbe, amelynek az egyik oldala kékre, a másik pirosra van festve. Ebből arra következtet, hogy ha vágna valaki egy lyukat egy tetszőleges (pl. gömb-) felületen, akkor azt be lehetne ragasztani ezzel a felülettel.

Meg fogjuk mutatni, hogy a bogárnak igaza van, a Möbius-szalag valóban átalakítható topológiai transzformációkkal úgy, hogy határvonala egy - eukíldeszi geometriai értelemben vett - körvonal legyen, igy beragasztható vele egy felületen, pl. gömbön vágott lyuk.

Ehhez először konstruálunk egy közbülső alakzatot, amelyről megmutatjuk, hogy ez egy Mőbius szalag, majd azt, hogy a határvonala körré deformálható.

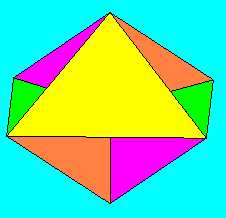
Vegyük egy oktaéder hat csúcsát, A, B, C, D, E -t, ezekből képezzük azt a felületet, amelyet az ABF , BCE , CDF , DAE háromszögek, valamint az AECF és BEDF négyszögek alkotnak.

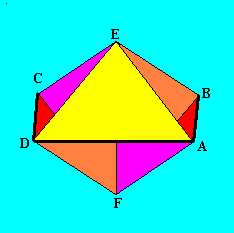
A két négyszögnek az EF szakaszra eső pontjai egybeesnek, azonban - az EF szakaszt a felület önátmetsző vonalának tekintve - ezeket a pontokat úgy tekintjük, hogy ezek különböző (az AECF, ill. a BEDF négyszögre illeszkedő) de egy helyen lévő pontok. Erre a jelenségre itt, és itt is láttunk már példát. A felület határvonala az ABCD négyszögvonal, amely - mint látni fogjuk - homeomorf a körrel.
Topológiailag ekvivalens un. homeomorf alakzatokhoz nem csak deformálással, hanem úgy is juthatunk, ha elvágjuk ugyan az alakzatot, de - a szükséges deformálást követően - ugyanott ugyanúgy össze is ragasztjuk. Ezt fogjuk most is tenni.

Vágjuk fel az alakzatot az AE , EC valamint a BF, FC szakaszok mentén.

 

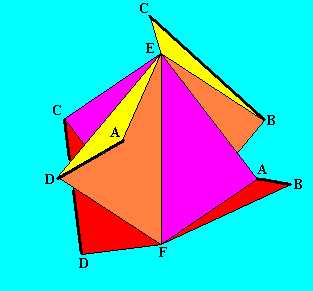
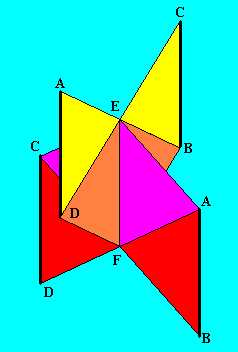
Mivel Az EF szakasz nem metszésvonal, hanem az önátmetszés helye, ezért az alakzat (AFB) , (AECF) ,(CDF) lapokból álló része elmozdítható a másik, (AED) , (BEDF) , (BCC) lapokból álló részéhez képest.

 

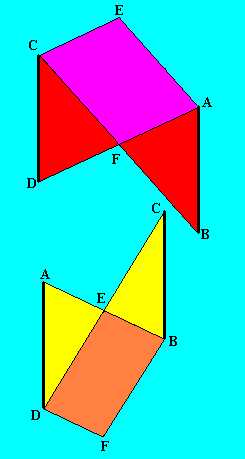
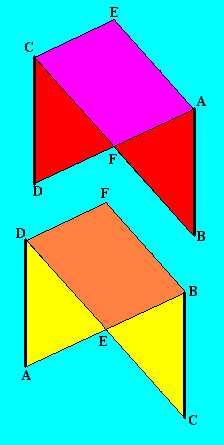
Ha most ezt a két részt ismét össze szeretnénk ragasztani ott, ahol elvágtuk: az AE , EC, ill. a BF, FD szakaszok mentén, akkor ehhez egy fél fordulatnyit csavarnunk kellene a szalagon, azaz Möbius-szalagot kapnánk. Ez pedig azt jelenti, hogy az eredeti alakzatunk valóban Möbius-szalag, hiszen mindvégig kizárólag topológiai átalakításokat végeztünk rajta.

Térjünk most vissza a Möbius-szalagnak ehhez a sokszögekből kialakított formájához!

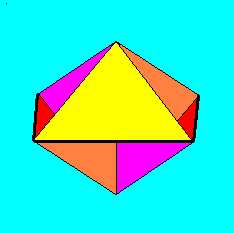
Ezt (folytonos deformálással) kissé kisimítva elérhetjük, hogy a kapott - önátmetsző - felület határvonala valóban kör legyen.

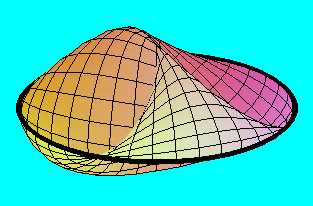
További deformálással az is elérhető, hogy ezzel pl. beragasszunk egy gömbön vágott lyukat,

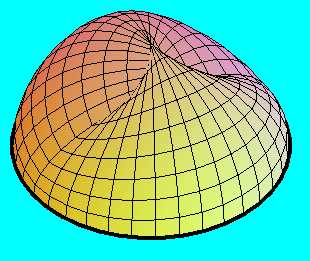
Két ilyen Möbius-szalagot egymással, vagy egy hengerpalást két végével összeeragasztva egy a szokásostól igencsak eltérő formájú Klein-kancsót kapunk.

Ha a kiindulásul vett sokszögekből álló alakzatunk határvonalát úgy szüntetjük meg, hogy felvesszük még az ABCD négyszöget is, akkor ezzel egy olyan zárt, határvonal nélküli felületet kapunk, amely ugyancsak egyoldalú (nem irányítható).

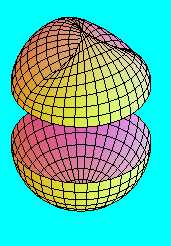
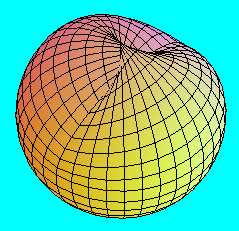
Ez a felület származtatható úgy is, hogy vágunk egy gömbön egy - kör alakú - lyukat, és ezt beragasztjuk egy Möbius-szalaggal. (Másképpen: összeragasztunk a határvonaluk mentén egy félgömböt és egy Möbius-szalagot.) Az így kapott felület természetesen különbözik mind a Möbius-szalagtól, mind a Klein-kancsótól.

Bebizonyítható, hogy a nem irányítható - más elnevezéssel egyoldalú - zárt, határvonal nélküli felületek mindegyike homeomorf az A1,   A2,   A3,   ... Ak,   ... felületek valamelyikével, ahol az Ak, felületet úgy származtatjuk, hogy vágunk a gömbön k darab "lyukat" , és ezeket rendre beragasztjuk egy-egy Möbius szalaggal. Eszerint a legutóbbi felület az   A1  , maga a Klein-kancsó - bárhogy realizáltuk is - az   A2 .

Ezek után látogatóinkra bízzuk annak a megítélését, hogy a változatosság, vagy ennek éppen az ellenkezője jellemzi a topológia világát, amelyből most csak egy pici ízelítőt nyújtottunk.

Rajzaink elkészítéséhez azonban itt is a "hagyományos" matematikai eszközöket használtuk. Aki dolgozott már a MAPLE matematikai programmal, első pillantásra észreveszi, hogy mind az itt bemutatott rajzok, mind a VRML fájlok ezzel készültek. (A VRML fájlok készítéséhez szükséges eszközöket csak a MAPLE V Release 5 verzió tartalmazza.)

Ezeket a felületeket előállító MAPLE fájlok tanulmányozásához megadjuk a MAPLE programok forrásfájljait, valamint azok azok text formátumát. Így lehetőséget adunk olvasóinknak arra, hogy a fájlokat letöltve tanulmányozhassák, módosíthassák azokat, az itt látott fogásokat alkalmazzák más felületek előállításában.
 

szalagok.mws            szalagok.txt
kancso.mws               kancso.txt
palack.mws                palack.txt
hosszmetszet.mws      hosszmetszet.txt
toruszbol.mws            toruszbol.txt
csavart.mws                csavart.txt
dupla.mws                  dupla.txt
oktaeder.mws              oktaeder.txt

Érdeklődő látogatóink további munkájához az önálló felfedezés örömét, jó munkát kíván: