A Fibonacci-sorozat A Fibonacci-sorozat és az aranymetszés A Fibonacci-négyzetek A Fibonacci-sorozat általánosítása – A Lucas-sorozat A geometriai sorozat és az aranymetszés
A Fibonacci-sorozat
A Fibonacci-sorozat és az aranymetszés
A Fibonacci-négyzetek
A Fibonacci-sorozat általánosítása – A Lucas-sorozat
A geometriai sorozat és az aranymetszés
A pizzai Leonardo a XII. és XIII. század fordulóján élt matematikus egyike volt azoknak, akik a hinduktól származó, de az akkori világban arab közvetítéssel elterjedő tízes alapú, helyi értékes rendszerre épülő számírási módot Európában meghonosították. Leonardo Pisano, ismertebb nevén Fibonacci kora matematikai ismereteit Liber Abaci címen ismert munkájában foglalta össze. E híres munkájában található a következő probléma, amit Fibonacci nyulaiként is gyakran emlegetnek:
Hány pár nyúlra szaporodik egy év alatt a kezdeti pár, ha tudjuk, a nyulak két hónap alatt válnak ivaréretté, és ezután minden pár minden hónapban egy új párnak ad életet és mindegyikük életben marad?
A feladat megoldásában a nyúl-párok számának időbeli alakulását kell követni. Az első hónapban egy nyúl-párunk van, és ugyanannyi lesz a másodikban is; a párok száma csak a harmadik hónapban változik egyről kettőre. A következő hónapban a szülők újabb párnak adnak életet, így a párok száma háromra nő. Az ötödik hónapban azonban már az új pár is szaporulatképes, így az új párok száma kettővel nő, és az összes párok száma ötre gyarapodik. A következő hónapban már mindkét ifjabb generáció hoz létre utódokat, és a párok száma hárommal növekedve nyolcra változik.
Az egyes hónapokhoz tartozó nyúl-párok számát leíró
1, 1, 2, 3, 5, 8, 13, 21, 34, …
számsor Fibonacci-sorozat néven vonult be a matematika történetébe. A sorozat előállításának alapja az a tulajdonság, mely szerint a harmadik elemtől kezdve bármely elem az előző kettő összege. A sorozat első két elemét azonban meg kell adni; ezek értéke a Fibonacci-sorozat esetén 1. A sorozat definíciója ennek megfelelően:
, 
és 
, ha n>2.
A sorozatok ilyen előállítási módját – mely az újabb elemek képzését az előzőekre vezeti vissza – rekurzív eljárásnak nevezik.
A Fibonacci-sorozat szoros kapcsolatban van az aranymetszéssel. Mint az előző
fejezetben már láttuk, érvényes az 
egyenlet az aranymetszésnek megfelelően felosztott szakasz esetében (ahol
a jelöli a szakasz teljes hosszát, x a hosszabbik metszetet).
Az aranymetszésnél a rövidebb és a hosszabbik metszet, valamint a felosztandó
szakasz olyan mértani sorozatot alkotnak, melynek hányadosa 
. Ezt az egyenletet pedig kapcsolatba hozhatjuk
a Fibonacci-sorozattal.
Jelöljük a továbbiakban 
-et q-val! A fenti egyenlőség mindkét oldalát 
-nal szorozva, ahol 
tetszőleges, zérustól különböző szám, az
egyenlőséget
kapjuk, ami éppen azt jelenti, hogy a fenti 
hányadossal képzett mértani sorozatokra igaz, hogy a harmadik elemtől
kezdve bármely elem egyenlő az előző kettő összegével.
Ez utóbbi tulajdonsága megvan a Fibonacci-sorozatnak is. Ugyanis a sorozat (n+1)-edik eleme (a harmadik elemtől) a következő módon állítható elő:
Mindkét oldalt a n-nel egyszerűsítve, az
egyenlethez jutunk.
A kapott összefüggés formailag hasonló az aranymetszésnél kapott egyenlethez, és (a harmadik elemtől) alkalmas a sorozat előállítására:
és így tovább.
A kapott összefüggés akkor egyezne meg az aranymetszési egyenlettel, ha a Fibonacci-sorozat egymást követő elemeinek hányadosa ugyanaz az érték lenne, vagyis az elemek geometriai sorozatot alkotnának.
A Fibonacci-sorozat elemei
azonban nem alkotnak mértani sorozatot, az egymást követő elemek hányadosa
nem állandó, ami különösen jól látszik alacsony sorszámok esetén. Az elemek
számának növelésével azonban ez a hányados egy állandó számhoz, a 
–hez közelít.
A közelítés kétoldali: két egymást követő elem hányadosa nagyobb, illetve kisebb, mint a közrefogott aranyszám.
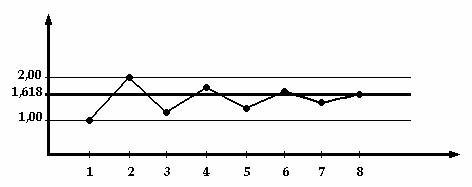
Írjuk fel a Fibonacci-sorozat elemeit és vizsgáljuk a két egymást követő tag hányadosának alakulását!
n
an
1
1
1
2
1
2
3
2
1,5
4
3
1,667
5
5
1,6
6
8
1,625
7
13
1,615
8
21
1,619
9
34
1,617
10
55
1,618
Ez a kétoldali közelítés más módon is világossá tehető. Ismeretes a mértani sorozatnak azon tulajdonsága, miszerint a második tagtól kezdve bármely elem az előtte lévő és őt követő elem mértani középarányosa. Ez másképpen fogalmazva azt jelenti, hogy a középső elem négyzete a vele közvetlenül szomszédos elemek szorzatával egyenlő. A Fibonacci-sorozat elemeire vonatkozóan ez a tulajdonság azzal a módosítással érvényesül, hogy a sorozat bármely elemének a négyzete (a másodiktól kezdve) a szomszédos elemek szorzatánál egyel kisebb vagy egyel nagyobb. Az elemek négyzetei és a szomszédos tagok szorzatai a következő táblázatról leolvashatók:
n
an
1 1 1
2
1 1
3
2 4
4
3 9
5
5 25
6
8 64
Általánosan:
az 
különbség –1, illetve +1 lesz, annak megfelelően, hogy n páros
vagy páratlan.
Azokat a négyzeteket, amelyek oldalainak mérőszámai a Fibonacci-sorozat elemei, Fibonacci-négyzeteknek nevezik. Az első n négyzet egymáshoz illesztésével olyan téglalapokat kapunk, melynek oldalhosszai megegyeznek az n-edik és az (n+1) -edik négyzet oldalának hosszával. Ha fn jelenti magát az n-edik négyzet oldalának hosszát, akkor ezek között a következő összefüggés áll fenn:
Az összefüggés helyessége a négyzetek illesztésével a következő módon látható be: vegyünk két egységnyi oldalhosszúságú négyzetet (F1 , F2) és ezek fölött helyezzük el a 2 egységnyi oldalhosszúságú F3 négyzetet. Az így kapott alakzathoz illesszünk (jobbról) olyan négyzetet, melynek oldalhossza megegyezik az előző két négyzet oldalának összegével (F4). Az így kapott téglalap fölé illesszük az F5, majd ezekhez ismét jobbról az F6 négyzetet, és így tovább.
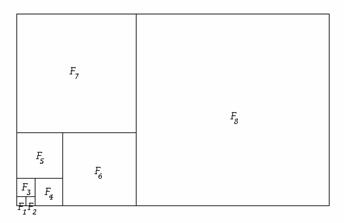
Az első két négyzet olyan téglalapot határoz meg, melyben az oldalak hosszúsága 1 és 2, vagyis amennyi az előző két négyzet oldalainak hossza. Az első három négyzet területösszege S3, olyan téglalapot határoz meg, melynek oldalai 2 és 3, és ezek éppen az F3 és F4 négyzetek oldalhosszaival egyeznek meg. Az összefüggés helyessége, mely a Fibonacci-sorozat tulajdonságából következik, az ábráról is leolvasható.
A Fibonacci-sorozat többféle
módon is általánosítható. Az általánosítás egyik módja olyan Fibonacci-típusú
sorozatok előállítása, melyeknél a rekurzivitási tulajdonságot változatlanul
hagyva, a sorozat első két elemét más értékekkel definiáljuk. Az ilyen módosított
sorozatot Lucas-sorozatnak nevezzük. A legfontosabb Lucas-sorozatok
az 
,
valamint az 
.
Megmutatható, hogy ennek a sorozatnak is megvan az a tulajdonsága, hogy két egymást követő elem hányadosa a tagok számának növelésével egy állandó számhoz tart, és ez az aranymetszési hányados.
A következő segédtétellel megmutatjuk, hogy minden Lucas-sorozat visszavezethető a Fibonacci-sorozatra.
Segédtétel:
Minden Lucas-sorozatra (
) és minden 
természetes számra érvényes, hogy
Bizonyítás:
A bizonyítást k-szerinti teljes indukcióval végezzük. Az indukció kezdése biztosított, ugyanis érvényes, hogy
és
Tegyük fel, hogy érvényes mindkét következő egyenlet:
és
A Lucas-sorozat meghatározott tulajdonságát kihasználva kapjuk a következőt:
Ha egy általános Lucas-sorozat
helyett a speciális (
) = (
) és (
) = (
) sorozatokat vizsgáljuk, a következőt kapjuk:
(1)
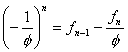(2)
Ebből következik:
A második egyenlőség is egyértelműen adja a következőt:
Ezen egyenlőségek segítségével állíthatók elő a híres Binet-formulák, amelyek egy explicit előállítása a Fibonacci-számoknak az aranymetszés segítségével.
Binet-formula:
Bármely n természetes számra érvényes:
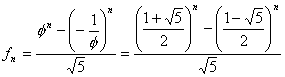
A formula érvényességét beláthatjuk, ha (1)-ből kivonjuk (2)-t:
.
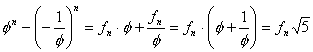Ebből pedig már egyértelműen látszik a Binet-fomula.
A geometriai sorozat egyik meghatározó tulajdonsága, hogy a második elemtől kezdve bármely eleme a két szomszédos elem mértani középarányosa:
Ha a geometriai sorozat
hányadosa az aranymetszésnek megfelelő növekedési arány (
), a sorozat harmadik elemétől kezdve igaz, hogy minden elem az előző kettő
összege. A középső elemet a-val jelölve:
.
A fenti összefüggés szerint az aranymetszési növekedési aránnyal, mint hányadossal képzett geometriai sorozat bármely eleméből a rákövetkező úgy is képezhető, hogy a kérdéses elemhez hozzáadjuk az azt megelőző elemet.
Hogyan értelmezhető ez
a tulajdonság az exponenciális függvény esetére? Mivel az exponenciális függvényt
minden valós számra értelmezzük, a fenti tulajdonság
az 
alakú exponenciális függvényre vonatkozóan azt jelenti, hogy ha annak alapja
az aranymetszésnek megfelelő növekedési arány,
akkor bármely valós x értékre fenn kell állnia a következő egyenlőségnek:
c·qx-1+c·qx=c·q
x+1.
Az egyenlet mindkét oldalát
kifejezéssel osztva (mivel 
és q>0), éppen az
,
az aranymetszés szerinti növekedést meghatározó egyenlethez jutunk.
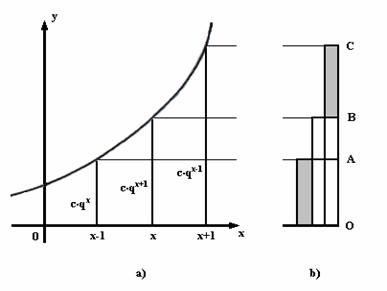
Legyen
most 
valós szám. Ha a 
,
és 
függvényértékeknek megfelelő távolságokat 
, 
és 
szakaszok jelölik. Az ábra b) részéről leolvasható, hogy a B pont
az 
szakaszt az aranymetszésnek megfelelő arányban osztja. Mivel 
, az A pont az
szakasznak szintén aranymetsző pontja.
Ha az idő függvényében leírt növekedési görbe olyan exponenciális függvény, melynek alapja az aranymetszési növekedési arány, akkor a növekedési folyamatban egy adott időponthoz tartozó állapotnak megfelelő érték aranymetszete az azt egy időegységgel megelőző és az azt ugyanannyival követő állapotok közötti növekedési szakasznak. A megelőző állapothoz tartozó érték aranymetszete a jelenleginek; ugyanakkor fennáll az az összefüggés is, hogy a meglévőt egy időegységgel követő állapotnak megfelelő érték a meglévő és az azt megelőző értékek összege.