Az aranyháromszög
Aranyháromszögből szabályos ötszög
A tízszög szerkesztése
Ötszög alkotása papírhajtogatással
![]() Az aranymetszés szerkesztése
Az aranymetszés szerkesztése
![]() 1. konstrukció
1. konstrukció
![]() 2. konstrukció
2. konstrukció
![]() 3. konstrukció
3. konstrukció
![]() 4. konstrukció
4. konstrukció
![]() 5. konstrukció
5. konstrukció
![]() 6. konstrukció
6. konstrukció
![]() Az ötszög szerkesztése
Az ötszög szerkesztése
![]() 1. konstrukció
1. konstrukció
Az aranyháromszög
Aranyháromszögből szabályos ötszög
![]() 2. konstrukció
2. konstrukció
![]() 3. konstrukció
3. konstrukció
A tízszög szerkesztése
![]() 4. konstrukció
4. konstrukció
![]() 5. konstrukció
5. konstrukció
Ötszög alkotása papírhajtogatással
![]() A pentagramma
A pentagramma
![]() A sík hézagmentes lefedése - Penrose csempéi
A sík hézagmentes lefedése - Penrose csempéi
![]() Az Amman-csíkok és a Beatty-sorozat
Az Amman-csíkok és a Beatty-sorozat
![]() Az aranyszög
Az aranyszög
![]() Az aranytéglalap
Az aranytéglalap
Valamely adott szakasz aranymetsző pontjának körzővel és vonalazóval való megszerkesztése már az ókorban ismert volt. A szerkesztés ezen változata azon a már akkor ismert tételen nyugszik, mely szerint a körhöz külső pontból húzott érintőszakasz mértani közepe a ponton átmenő szelő körrel alkotott metszeteinek.
Szerkesszük meg adott ![]() szakasznak azt a belső S pontját, mely a szakaszt az aranymetszésnek
megfelelő arányban osztja! A szerkesztés első lépéseként vegyünk fel egy,
a B ponton átmenő, az (AB) egyenesre merőleges egyenest, és
mérjük fel erre a B pontból kiindulva
szakasznak azt a belső S pontját, mely a szakaszt az aranymetszésnek
megfelelő arányban osztja! A szerkesztés első lépéseként vegyünk fel egy,
a B ponton átmenő, az (AB) egyenesre merőleges egyenest, és
mérjük fel erre a B pontból kiindulva ![]() távolságot. Ennek O végpontjából, mint középpontból szerkesszünk
távolságot. Ennek O végpontjából, mint középpontból szerkesszünk
![]() sugarú kört.
sugarú kört.
E körnek a B ponthoz tartozó érintője az (AB)
egyenes lesz. Szerkesszük meg az [AO) félegyenest. E félegyenesnek
a körrel való metszéspontjai E és F pontok. A B pontot
összekötve ezekkel a metszéspontokkal, az ABE és ABF háromszögeket
kapjuk. Mivel a két háromszög A csúcsnál lévő szöge közös, továbbá
az ![]() és
és ![]() a BE ívhez tartozó kerületi szögek, és így egyenlők, a kapott háromszögek
hasonlók. A hasonlóságból a megfelelő oldalak arányát felírva:
a BE ívhez tartozó kerületi szögek, és így egyenlők, a kapott háromszögek
hasonlók. A hasonlóságból a megfelelő oldalak arányát felírva:
![]() ,
,
amiből az ![]() egyenlethez jutunk.
egyenlethez jutunk.
Ezt átrendezve az ![]() egyenletet kapjuk, ami éppen azt fejezi ki, hogy az x hosszúságú
egyenletet kapjuk, ami éppen azt fejezi ki, hogy az x hosszúságú
![]() szakasz mértani középarányos a teljes
szakasz mértani középarányos a teljes ![]() szakasz és annak rövidebb metszete között. Ha
szakasz és annak rövidebb metszete között. Ha ![]() szakaszt az A pontból
szakaszt az A pontból ![]() -re rámérjük, a kapott S pont az
-re rámérjük, a kapott S pont az ![]() szakaszt éppen az aranymetszés szerint osztja.
szakaszt éppen az aranymetszés szerint osztja.
Ez a szerkesztés lényegében azonos az előzővel, csupán indoklásában tér el attól.
Szintén adott ![]() szakasz S aranymetsző pontját keressük. A szerkesztés menete is megegyezik
az előzőével: Első lépésként állítsunk merőlegest erre a szakaszra a B
végpontjában, és mérjük fel erre a merőlegesre
szakasz S aranymetsző pontját keressük. A szerkesztés menete is megegyezik
az előzőével: Első lépésként állítsunk merőlegest erre a szakaszra a B
végpontjában, és mérjük fel erre a merőlegesre ![]() -t. A kapott végpontot nevezzük C-nek. Mivel a
-t. A kapott végpontot nevezzük C-nek. Mivel a 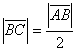 , és
, és ![]() , az A, B és C pontok által alkotott háromszög egy
derékszögű háromszög, melynek átfogója
, az A, B és C pontok által alkotott háromszög egy
derékszögű háromszög, melynek átfogója ![]() .
.
Következő
lépésként mérjük fel ![]() -t az
-t az ![]() -re és az így kapott pontot nevezzük D-nek. Ekkor
-re és az így kapott pontot nevezzük D-nek. Ekkor
![]()
és
![]() .
.
Felmérve ![]() -t
-t ![]() -re és a kapott pontot S-nek nevezve el:
-re és a kapott pontot S-nek nevezve el: ![]() , amiből következik, hogy
, amiből következik, hogy
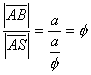 , azaz S az
, azaz S az ![]() szakasz aranymetsző pontja.
szakasz aranymetsző pontja.
E konstrukcióban szintén adott ![]() szakasz S aranymetsző pontját keressük
szakasz S aranymetsző pontját keressük
Az előző szerkesztéshez első lépéséhez hasonlóan most is
egy ![]() hosszúságú merőleges szakaszt kell állítanunk az
hosszúságú merőleges szakaszt kell állítanunk az ![]() szakasz egyik végpontjába. Ezúttal az A pontot szemeljük ki e célra,
a merőleges szakaszunk végpontját pedig jelöljük C-vel! Ezzel szintén
egy olyan derékszögű háromszöget szerkesztettünk, melynek átfogója
szakasz egyik végpontjába. Ezúttal az A pontot szemeljük ki e célra,
a merőleges szakaszunk végpontját pedig jelöljük C-vel! Ezzel szintén
egy olyan derékszögű háromszöget szerkesztettünk, melynek átfogója ![]() .
.
A következő lépésben térünk el lényegében az előző szerkesztés
menetétől: C-ből mint középpontból messük el [CA) félegyenest
egy ![]() sugarú körívvel; a metszéspontot jelöljük D-vel. Ekkor igaz a következő:
sugarú körívvel; a metszéspontot jelöljük D-vel. Ekkor igaz a következő:
![]()
Ezután
A-ból ![]() sugarú körívvel messük
sugarú körívvel messük ![]() -t! Bizonyítandó, hogy ez a metszéspont éppen a keresett S, az
-t! Bizonyítandó, hogy ez a metszéspont éppen a keresett S, az ![]() aranymetsző pontja. Ezt egyszerűen beláthatjuk:
aranymetsző pontja. Ezt egyszerűen beláthatjuk:
![]()
amiből pedig következik, hogy
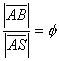 , azaz S az
, azaz S az ![]() szakasz aranymetsző pontja.
szakasz aranymetsző pontja.
Ezt a szerkesztést majdnem 20 éve ismerjük George Odom
jóvoltából. Az 1983-ban az American Math Monthly-ban megjelent feladata
így szól: Legyenek A és B a EFG egyenlő oldalú háromszög
![]() és
és ![]() oldalainak felezőpontjai.
oldalainak felezőpontjai. ![]() egyenese metszi a háromszög körülírható körét C-ben és D-
ben. Mutassuk meg, hogy B az
egyenese metszi a háromszög körülírható körét C-ben és D-
ben. Mutassuk meg, hogy B az ![]() aranymetsző pontja!
aranymetsző pontja!
Legyen ![]() . Ekkor
. Ekkor ![]() , ami abból következik, hogy
, ami abból következik, hogy ![]() az EFG háromszög középvonala, aminek egyenese, metszi a háromszög
köré írható körét C és D pontokban. Ekkor
az EFG háromszög középvonala, aminek egyenese, metszi a háromszög
köré írható körét C és D pontokban. Ekkor ![]() .
.
Ekkor megfordítva a húr-tételt:
![]()
Innen pedig egyből adódik a már jól ismert egyenlet:
![]() , ahol
, ahol ![]() .
.
Visszatérve az eredeti jelölésekhez: 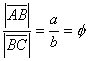 , ami azt jelenti, hogy B éppen az
, ami azt jelenti, hogy B éppen az ![]() aranymetsző pontja.
aranymetsző pontja.
Az előző konstrukciókban az adott szakasznak olyan belső pontját kerestük, amely aranymetszésben osztja a szakaszt. Most adott szakaszhoz olyan külső pontot szerkesztünk, amellyel a szakasz hossza, valamint a pont és szakasz között lévő távolság egymással aranymetszést alkotnak.
Tekintsük az ![]() szakaszt! Ennek felezőpontját jelöljük E-vel.
szakaszt! Ennek felezőpontját jelöljük E-vel. ![]() egyenesére állítsunk merőlegest S-ben és erre a merőlegesre mérjük
fel
egyenesére állítsunk merőlegest S-ben és erre a merőlegesre mérjük
fel ![]() -t! Az így kapott pontot nevezzük C-nek! Ekkor
-t! Az így kapott pontot nevezzük C-nek! Ekkor ![]() . Mivel
. Mivel 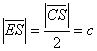 és
és ![]() , ezért
, ezért
![]() .
.
Az E középpontú ![]() sugarú kör az
sugarú kör az ![]() egyenesét két pontban metszi. Az S-hez közelebbi metszéspontot jelöljük
B-vel!
egyenesét két pontban metszi. Az S-hez közelebbi metszéspontot jelöljük
B-vel!
Bizonyítandó, hogy S az ![]() aranymetsző pontja. Ez az állítás a következőképpen igazolható:
aranymetsző pontja. Ez az állítás a következőképpen igazolható:
![]() ,
,
amiből következik, hogy
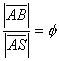 .
.
Az előző konstrukciókban adott szakasz belső illetve külső aranymetsző pontját szerkesztettük. Most adott aranymetszett szakaszhoz szerkesztünk további belső, illetve külső aranymetszéseket.
Legyen adott egy ![]() szakasz, melynek S az aranymetsző pontja. Az A középpontú
szakasz, melynek S az aranymetsző pontja. Az A középpontú
![]() sugarú kör (AB) egyenesét metszi egy
sugarú kör (AB) egyenesét metszi egy ![]() -n kívüli pontban, C-ben.
-n kívüli pontban, C-ben.
Igazolandó, hogy A a ![]() aranymetsző pontja.
aranymetsző pontja.
Mivel S az ![]() aranymetsző pontja, és
aranymetsző pontja, és ![]() , ezért
, ezért ![]() , amiből következik, hogy:
, amiből következik, hogy:
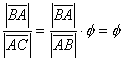 ,
,
ami éppen azt jelenti, hogy A a ![]() aranymetsző pontja.
aranymetsző pontja.
Ezzel a módszerrel adott aranymetszett szakaszhoz akár külső, akár további belső osztópontokat könnyedén szerkeszthetünk:
Ezen szerkesztési módszerek ismeretében most már könnyűszerrel szerkeszthetünk aranymetsző pontot bármelyik szakaszhoz. Hogy mire is jó ez nekünk?
Létezik két olyan síkidom, amely szerkesztéséhez nélkülözhetetlen az aranymetszés megszerkesztésének ismerete. Ez a két síkidom a szabályos öt-, illetve tízszög.
A pentagon szögeinek nagysága 72°, ami azt jelenti, hogy szerkesztése nem olyan egyszerű, mint a 60°, vagy annak többszörösei. Általános és középiskolában az ötszög szerkesztése nem is része a tananyagnak. Sain Márton a következőképp vélekedik az ötszög szerkesztéséről:
„A szabályosötszög-szerkesztés feladata szinte összefoglalja mindazon alapvető
számelméleti és geometriai ismereteket, amelyekkel a püthagoreusok már rendelkeztek.”
Az ötszög szerkesztése történelmi távlatban is bonyolult. Euklidesz is messziről indul. Először olyan háromszöget szerkeszt, melynek alapjánál lévő két szöge kétszer akkora, mint a csúcsában lévő szög, azután ezt a háromszöget illeszti adott sugarú körbe, s bizonyítja, hogy az így körbe írt ötszög szabályos.
Ez a szerkesztés két részből áll. Az első részében egy olyan egyenlőszárú háromszöget kell szerkesztenünk, melynek az alapon nyugvó szögei kétszer akkorák, mint a csúcsnál lévő szög. A második részben ezt a háromszöget adott sugarú körbe kell elhelyezni úgy, hogy szabályos ötszöget eredményezzen.
Euklidesz Elemeinek negyedik könyvének 10. feladata a következőképpen hangzik:
„Oly egyenlő szárú háromszöget állítani össze, melynek talpánáli mindenik szeglete kétakkora legyen, mint a harmadik szeglete.” [1]
Ez a konstrukció első része.
Legyen ![]() olyan szakasz, melynek C az aranymetsző pontja. Első lépésként
A középponttal, és
olyan szakasz, melynek C az aranymetsző pontja. Első lépésként
A középponttal, és ![]() sugárral szerkesszük meg K kört. Ezt a kört messük egy B
középpontú,
sugárral szerkesszük meg K kört. Ezt a kört messük egy B
középpontú, ![]() sugarú körívvel, és a metszéspont legyen D. Húzzuk meg
sugarú körívvel, és a metszéspont legyen D. Húzzuk meg ![]() és
és![]() szakaszokat, és az
szakaszokat, és az ![]() körülírható körét, k-t. Be kell látnunk, hogy az
körülírható körét, k-t. Be kell látnunk, hogy az ![]() megoldása a feladatnak, azaz az alapon fekvő szögei éppen kétszeresei a
csúcsnál lévő szögnek.
megoldása a feladatnak, azaz az alapon fekvő szögei éppen kétszeresei a
csúcsnál lévő szögnek.
Mivel C az ![]() aranymetsző pontja, azaz
aranymetsző pontja, azaz ![]() és
és ![]() , ezért
, ezért
![]()
„És minthogy ACD (k) körön kívül vétetett
némi B pont, és B-től ACD körre ![]() és
és![]() két egyen van vonva, melyeknek egyike szeli a kört, másika találkozik vele”,
és
két egyen van vonva, melyeknek egyike szeli a kört, másika találkozik vele”,
és ![]() :
:
tehát ![]() érinti k kört.
érinti k kört.
Ezért, és mert ![]() egyik végpontja a D:
egyik végpontja a D:
![]()
Mindkét szöghöz hozzáadva ![]() -et, kapjuk:
-et, kapjuk:
![]()
Mivel ![]() nagysága a
nagysága a ![]() külső szög nagyságával egyenlő, így
külső szög nagyságával egyenlő, így
![]()
Mivel ![]() , így
, így ![]() , amiért
, amiért ![]() , azaz
, azaz
![]() .
.
Minthogy ![]() ,
, ![]() . De
. De ![]() , ezért
, ezért ![]() , ami miatt
, ami miatt ![]() .
.
Ami nem jelent mást, mint hogy ![]() , azaz
, azaz ![]() . Mivel
. Mivel ![]() , így ezek mindegyike kétszer akkora, mint
, így ezek mindegyike kétszer akkora, mint ![]() .
.
„Állíttatott tehát ABD egyenlőszárú háromszög, melynek BD talpnál való mindenik szeglete kétakkora, mint a harmadik.” [2]
Ezt a háromszöget, mert oldalainak aránya ![]() , aranyháromszögnek is nevezik. (Alapját a-val jelölve, szárai
, aranyháromszögnek is nevezik. (Alapját a-val jelölve, szárai ![]() hosszúságúak.) Belsőszögeinek nagysága rendre 72°, 72° és 36°.
hosszúságúak.) Belsőszögeinek nagysága rendre 72°, 72° és 36°.
Ezzel a konstrukció első része készen van. A következő részében azt nézzük meg, hogyan lesz ebből az aranyháromszögből szabályos ötszög.
Euklidesz Elemeinek negyedik könyvében a 11. feladat a következőképp hangzik:
„Adott körbe egyenlő oldalú és egyenlő szegletű ötszeget írni.” [3]
Adott K kör és FGH aranyháromszög, melynek
a G és H csúcsoknál lévő szögei kétszer akkorák, mint az
F csúcsnál lévők. Írjunk a K körbe olyan – az ![]() -gel hasonló –
-gel hasonló – ![]() -et úgy, hogy
-et úgy, hogy ![]() legyen. Miután megszerkesztettük ezt az
legyen. Miután megszerkesztettük ezt az ![]() -et, messük K körvonalat az
-et, messük K körvonalat az ![]() , illetve a
, illetve a ![]() belső szögfelezőivel E és B pontokban, majd kössük össze
az így kapott ABCDE konvex ötszög csúcspontjait.
belső szögfelezőivel E és B pontokban, majd kössük össze
az így kapott ABCDE konvex ötszög csúcspontjait.
Mivel ![]() , valamint [CE) és [DE) felezik ACD, illetve CDA
szögeket, ezért
, valamint [CE) és [DE) felezik ACD, illetve CDA
szögeket, ezért
![]()
Mivel mindegyik kerületi szög, és mindegyik egyenlő nagyságú és mivel azonos nagyságú kerületi szögekhez azonos hosszúságú ívek tartoznak, ezért
![]()
Ugyanazon körben azonos hosszúságú ívekhez azonos hosszúságú húrok feszítenek, tehát
![]()
Azaz az ABCDE ötszög egyenlő oldalú ötszög. Már csak azt kell igazolni, hogy szögei is egyenlő nagyságúak.
Induljunk ki az előbbi megállapításból, miszerint ![]() . Adjuk hozzájuk a közös
. Adjuk hozzájuk a közös ![]() ívet. Ekkor
ívet. Ekkor ![]() . Ehhez a két ívhez két kerületi szög is tartozik:
. Ehhez a két ívhez két kerületi szög is tartozik:
![]()
Ugyanezért igaz a következő is:
![]()
Ezzel „meg van mutatva, hogy ABCDE ötszeg egyenlő szegletű, meg van mutatva az is, hogy egyenlő oldalú. Adott körbe tehát sat.” [4] .
Ez a szerkesztés egy picivel egyszerűbb, mint az előző. Most is egy aranyháromszögből induljunk ki! A szerkesztés menetének leírása az előző konstrukcióban megtalálható, azonban a második része eltér attól.
Mint már az előbb láttuk, az aranyháromszög alapja a szabályos ötszög egyik oldalával megegyezik, vagyis a szerkesztendő ötszög oldala és az aranyháromszögünk alapja egyenlő nagyságú szakaszok. Ebből a tulajdonságból pedig könnyen adódik a következő:
Legyen ![]() a szóban forgó aranyháromszög, melynek alapja a
a szóban forgó aranyháromszög, melynek alapja a ![]() szakasz. C és D pontokból körívezzünk
szakasz. C és D pontokból körívezzünk ![]() sugarú ívvel, majd ismételjük meg ezt az A csúcsnál is. Ekkor a háromszög
mindkét száránál kaptunk egy-egy metszéspontot, amiket nevezzünk rendre
B és E pontoknak.
sugarú ívvel, majd ismételjük meg ezt az A csúcsnál is. Ekkor a háromszög
mindkét száránál kaptunk egy-egy metszéspontot, amiket nevezzünk rendre
B és E pontoknak.
Triviális, hogy ABCDE ötszög minden oldala egyenlő.
Euklidesz Elemeinek negyedik könyvének 11. feladata úgy szólt, hogy adott körbe szabályos ötszöget kellett írni. Ezt ő a már vázolt módon oldotta meg. Most e feladat egy másik megoldásáról lesz szó, melyben egy másik szabályos sokszögön, a tízszögön keresztül jutunk el a pentagon megszerkesztéséhez.
Ez a megoldás a következő tételen alapszik:
A szabályos tízszög oldala annak az aranymetszésnek a kisebbik szelete, amelynek a nagyobbik szelete a kör sugara. [5]
E tétel alapján a kör sugarából kiindulva a szabályos tízszög oldalát, és így a körbe írt szabályos tízszöget is megszerkeszthetjük. A tízszög minden második csúcsát összekötve a beírt szabályos ötszöget is megkapjuk.
Ha az ábrát alaposabban szemügyre vesszük, egyből feltűnik,
hogy az ![]() egy olyan derékszögű háromszög, mely befogóinak aránya 2:1, átfogója éppen
ezért
egy olyan derékszögű háromszög, mely befogóinak aránya 2:1, átfogója éppen
ezért ![]() , ami azt jelenti – lásd korábban az aranymetszés szerkesztésének 1. konstrukcióját
– , hogy:
, ami azt jelenti – lásd korábban az aranymetszés szerkesztésének 1. konstrukcióját
– , hogy:
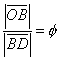 ,
,
azaz ![]() annak az aranymetszésnek a kisebbik szelete, melynek nagyobbik szelete
az adott kör sugara. Ebből pedig következik, hogy
annak az aranymetszésnek a kisebbik szelete, melynek nagyobbik szelete
az adott kör sugara. Ebből pedig következik, hogy ![]() a körbe írható tízszög oldalával egyenlő hosszúságú.
a körbe írható tízszög oldalával egyenlő hosszúságú.
A kapott tízszög minden második csúcspontját összekötve pedig eljutunk az adott körbe írható szabályos ötszöghöz.
E konstrukció hasonló az előzőhöz, tulajdonképpen annak egy „továbbfejlesztett” változata.
A következő tételt vesszük alapul:
A kör sugarával és a körbe írt szabályos tízszög oldalával, mint befogókkal szerkesztett derékszögű háromszög átfogója a körbe írt szabályos ötszög oldala [6] .
E tétel is módot nyújt a körbe írt szabályos ötszög oldalának megszerkesztésére, ha egyszer a beírt szabályos tízszög oldalát már megszerkesztettük.
Az előző szerkesztésből kiindulva itt is feltűnik, hogy
![]() a körbe írható szabályos tízszög oldalával egyenlő nagyságú. Mivel
a körbe írható szabályos tízszög oldalával egyenlő nagyságú. Mivel ![]() és
és ![]() , következik, hogy
, következik, hogy ![]() . Ekkor
. Ekkor ![]() egy olyan derékszögű háromszög, melynek befogói a körbe írható tízszög
oldala, illetve a kör sugara, így átfogója (
egy olyan derékszögű háromszög, melynek befogói a körbe írható tízszög
oldala, illetve a kör sugara, így átfogója (![]() ) a körbe írható szabályos ötszög oldalával egyenlő nagyságú.
) a körbe írható szabályos ötszög oldalával egyenlő nagyságú.
Ez a konstrukció egy kissé rendhagyó módja a szerkesztésnek. Igazából nem is szerkesztés, ezért inkább az ötszög „létrehozásának” nevezném. Az előző szerkesztések igazolásához szükség van felsőbb matematikai ismeretekre, ez a módszer azonban beilleszthető az általános iskolai tananyagba is, ha másképp nem, de szakköri szinten mindenképpen.
Ehhez mindösszesen egy papírcsíkra van szükségünk. A művelet nem más, mint egy csomó kötése erre a csíkra. Ha szépen kisimítjuk ezt a „csomót”, megfigyelhetjük, és igazolhatjuk, hogy tényleg egy szabályos ötszöget alkottunk.

Az igazolást – hogy tényleg szabályos ötszöget alkottunk – szintén a legegyszerűbb módszerekkel végezzük. Az ötödik fázisban bemutatott hajtással lemérhető bármelyik oldal – elegendő hosszúságú papírcsík birtokában –, hogy minden oldal egyenlő nagyságú. Az ötszög szögeinek egyenlő nagyságát pedig a már jól bevált – szintén papírhajtogatásos – módszerrel igazolhatjuk. Ha ezt a hajtogatott ötszöget a szimmetriatengelyei mentén félbehajtjuk, azt tapasztaljuk, hogy a szögek fedik egymást. Ebből pedig az következik, hogy a hajtogatott síkidomunk szabályos ötszög.
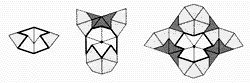
Figyeljük meg az 5. ábrát! Ahol a papírcsík kettő, illetve több rétegben fordul elő, egy érdekes síkidom válik láthatóvá. Ez a síkidom nem más, mint az oly sokat emlegetett, és szimbólumként gyakran használt pentagramma.
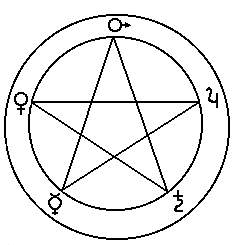
Az ókori időktől kezdve az ötös számnak és így az ötszögnek is különös jelentőséget tulajdonítottak. Jelzői fokozás nélküli szuperlatívuszok: a csodálatos ötszög, a bűvös ötszög, a misztikus ötszög. A csillagötszög napjainkban is igen „közkedvelt” szimbólum. A Gonosztól a Jóig mindenféle ideológiát vonultatnak fel égisze alatt. A középkor asztrológiai ábráin az ötszög csúcsainál az öt főbolygó (Merkur, Vénusz, Mars, Jupiter, Szaturnusz) neve szerepel. Az ötszög, mint jelkép már az ősidőktől fogva az egység, és ugyanakkor az univerzum szimbóluma, de jelképe a termékenységnek és az életnek is. Az ötágú csillag jele például a szabadkőműveseknek, de ki ne emlékezne arra a bizonyos vörös színűre?

A boszorkányszöget „titkos” jelként a boszorkányok és az okkultista tanok ismerői használják; de volt egy ezeknél is fontosabb csoport, akik mind a tudományos életben, mind a filozófiában jelentős szerepet játszottak.
Ők a püthagoreusok. Az ötöt a mikrokozmosz tökéletes számának tartották, a pentagrammát pedig titkos jelként használták, bár már Babilonban is ismert volt. Az egészség szimbólumát látták benne és csúcsaihoz az egészség istennőjének, Hügiéniának jeleit kapcsolták. A csodálatos ötszög segítségével értelmezték az aranymetszés törvényét is, amely szerint a csillagötszög arányai az aranymetszés törvényeinek sorozata.
A pentagramma tulajdonképpen nem más, mint öt darab aranyháromszög egy ötszög köré rendezve. Ha egy csillagötszöget testhálóként értelmezünk, egy szabályos ötszög alapú gúlát vélhetünk felfedezni benne. Ha ilyen gúlákat illesztünk egy dodekaéder lapjaira, ún. csillag poliédert, mégpedig kis csillag dodekédert kapunk eredményül.

Roger Penrose oxfordi matematikus 1973-ban fedezte fel a sík nem periodikus parkettázásának lehetőségét. Martin Gardner által vált ismertté ez a felfedezés, amely 1977 januárjában jelent meg a Scientific American-ben Matematikai játékok címen. A 80-as évek elején ismét központi témává vált, 3 dimenzióra történő álalánosításának következtében, valamint a kristálykutatásban jelentős felfedezéseknek köszönhetően (felfedezték a kvázi-kristályokat).
Penrose-csempék alakja különféle lehet, de a legérdekesebb és legismertebb pár a dárdák (konkáv rész) és sárkányok (konvex rész) kettőse. A csempék aranyrombuszokból készíthetőek, melyek szögeiknek nagysága 72° és 108°.
Ha felosztjuk a rombusz hosszabbik átlóját az aranymetszés
szerint és az aranymetsző-pontot összekötjük a tompaszögű csúcsokkal, és e
két szakasz mentén kettévágjuk a rombuszt, egy konvex és egy konkáv, de egymással
páronként megegyező oldalhosszúságú deltoidot kapunk. Oldalhosszainak aránya
éppen ![]() . (Ennek igazolásához emlékezzünk vissza az aranyháromszögre, vagy egy szabályos
ötszög átlóira.)
. (Ennek igazolásához emlékezzünk vissza az aranyháromszögre, vagy egy szabályos
ötszög átlóira.)
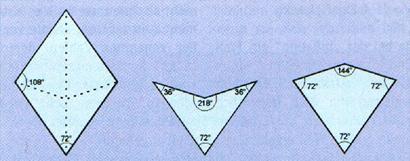
A rombusszal periodikusan csempézhető a sík, ezért így nem illeszthetők össze a csempék. (Hiszen a probléma az aperiodikus csempézés.) Hogy még csak véletlenül se essünk abba a hibába, hogy rombusszal csempézünk, meg kell jelölni az össze illeszthető csúcsokat, például különböző színű pöttyökkel.

A szabályunk az, hogy összeillesztéskor minden csúcsnak
ugyanolyan színű csúcshoz kell csatlakoznia. Ahhoz, hogy teljes mértékben
kiélvezhessük a Penrose-csempézés szépségeit és rejtélyeit, legalább 100
sárkányra és 60 dárdára van szükségünk. A darabokat csak az egyik oldalukon
kell kiszínezni. A kétféle alakzat darabszámának aránya (területük arányához
hasonlóan) egyenlő az aranymetszés arányszámával. Azt hihetnénk, hogy a kisebb
dárdából van szükség több darabra, de ez éppen fordítva van. Sárkányból ![]() -szer annyi kell, mint dárdából. Végtelen csempézés esetén ez a szám a pontos
arányt adja meg.
-szer annyi kell, mint dárdából. Végtelen csempézés esetén ez a szám a pontos
arányt adja meg.


A csempézés aperiodikusságát Penrose a ![]() irracionalitásával bizonyítja; hiszen ha periodikus lenne; akkor az aránynak
nyilvánvalóan racionálisnak kellene lennie.
irracionalitásával bizonyítja; hiszen ha periodikus lenne; akkor az aránynak
nyilvánvalóan racionálisnak kellene lennie.
Bizonyítható, hogy a Penrose-csempézések száma az egyenes pontjainak számosságához hasonlóan nem megszámlálható. A bizonyítások egy meglepő jelenségen alapulnak. Ezt a jelenséget felfújásnak nevezzük, mert bármelyik alakzat előállítható kisebb elemekből:
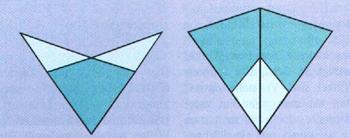
Két fél dárdából és egy sárkányból egy új, nagyobb dárda hozható létre, míg két fél dárdából és két sárkányból egy új, nagy sárkány állítható elő. Ugyanez visszafelé is működik: minden elemből levághatók olyan részek, amelyekből sárkány és dárda rakható össze, továbbá a megmaradó részek is sárkányok illetve nyilak lesznek. (Ezt az inverz műveletet leeresztés nek nevezzük.)
Egy tehetséges fiatal matematikus, Robert Ammann, aki alacsony szintű számítógépes munkákat végzett Massachusetts-ben, Penrose-tól függetlenül felfedezte a rombusz-csempéket 1976-ban. Ammann hamarosan rájött, hogy mindkét csempepár olyan mintákhoz vezet, melyeket öt, párhuzamos egyenesekből álló egyenescsalád határoz meg, ahol az egyenesek öt különböző irányban haladnak át a síkon, 360/5=72 fokos szögben metszve egymást. Egy ilyen egyenescsalád – mai elnevezéssel Ammann-csíkok – látható az ábrán.

Észrevehető, hogy az egyenesek olyan dárdák konkáv csúcsán haladnak át, melyek egyik része egy irányba, a többi pedig ellenkező irányba mutat. Szigorú értelemben ez nem pontos meghatározás az egyenesek elhelyezkedésére, de a mi céljainknak ez az egyszerű szabály is megfelel. A precíz meghatározás a Grünbaum–Shephard-könyvben megtalálható. Ha a pontos helyükre kerülnek az egyenesek, akkor mindegyik egy hajszálnyival a dárdák konkáv csúcsán kívül halad. A minta minden szabályos tízszögének belsejében tökéletes pentagrammát rajzolnak ki az Ammann-csíkok.
A szomszédos egyenesek között kétféle távolság figyelhető meg, az egyiket H-val (hosszabb), a másikat R-rel (rövidebb) fogjuk jelölni. Ha megfelelően helyezzük el az egyeneseket, akkor a két távolság aranymetszéssel aránylik egymáshoz. Ráadásul a teljes síkot tekintve az egy családon belül levő csíkok között a H-k számának aránya a R-ek számához szintén aranymetszés. Ha elindulunk a csíkok egyik családjára merőleges irányban, H-k és R-ek sorozatával jegyezhetjük le az egymást követő távolságokat. Ez a sorozat nem lesz periodikus, és a Penrose-csempézésnek szép, egydimenziós megfelelőjét adja, teljesül rá a lokális izomorfizmus-tétel. Bármilyen véges részét kiválasztva a sorozatnak, mindig meg fogjuk találni a közelben annak másolatát. Induljunk el bárhol és jegyezzünk fel akárhány betűt véges sok, mondjuk egymilliárd lépésen keresztül. A sorozat bármelyik pontjáról elindulva biztosak lehetünk abban, hogy elérünk egy ugyanilyen egymilliárd betűs sorozatot. Csak akkor nem ismétlődik meg a betűsorozat, ha végtelen
Conway felfedezte, hogy ez a sorozat a következőképpen kapható meg az aranymetszésből. Írjuk fel növekvő sorrendben az aranymetszés arányszámának ((1+51/2)/2) a többszöröseit, lefelé kerekítve a legközelebbi egész számra. A kapott sorozat így fog kezdődni: 1, 3, 4, 6, 8, 9, 11, 12, 14, 16, 17, 19, 21, 22, 24, 25, 27, 29, 30, 32, 33, 35, 37, 38, 40, 42, 43, 45, 46, 48, 50, ... Ez a 917-es számú sorozat N. J. A. Sloane: Handbook of Integer Sequences (Egész számokból álló sorozatok kézikönyve) című könyvében. Ha az aranymetszés négyzetének a többszöröseit kerekítjük le, akkor a 2, 5, 7, 10, 13, 15, 18, 20, 23, ... sorozatot kapjuk. A két sorozatot szokás egymás "komplementerének" nevezni. A kettő egyesítésében minden pozitív egész egyszer és csak egyszer fordul elő. Ha egy tetszőleges a valós szám többszöröseit kerekítjük lefelé a legközelebbi egészre, akkor az így kapott sorozatot az a spektrumának nevezik. Ha a irracionális, akkor szokás a sorozatot Beatty-sorozatnak hívni, Samuel Beatty kanadai matematikus neve után, aki az ilyesfajta sorozatokra irányította a figyelmet 1926-ban. Az aranymetszésen alapuló komplementer Beatty-sorozatok szolgáltatják a NIM-játék Wythoff-játéknak nevezett híres változatának nyerő stratégiáját.
Az aranymetszéses Beatty-sorozat szomszédos tagjainak különbsége vagy 1, vagy 2. Ha felírjuk az első különbségsorozatot, majd minden 1-est 0-ra és minden 2-est 1-re változtatunk, egy végtelen bináris sorozatot kapunk, amely így kezdődik: 101101011011010... Ez az Ammann-csíkok bármelyik végtelen családjában az R-ek és H-k sorozatának egy darabja. Conway a "zenei sorozat" kifejezést használja az aranymetszéses sorozat bármelyik véges szakaszára.
Az ilyen sorozatok számos érdekes tulajdonsággal rendelkeznek, ha például a fenti, binárisan megadott Fibonacci-sorozat elé tizedesvesszőt rakunk, akkor az eredmény egy olyan irracionális szám kettes számrendszerbeli vesszőstört alakja lesz, melyet a következő lánctört határoz meg:
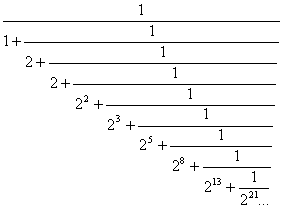
A lánctörtben szereplő kitevők éppen a Fibonacci-számok. Conway számos publikálatlan eredménnyel rendelkezik arról, hogy a Penrose-csempézések hogyan függenek össze a Fibonacci-számokkal, amik viszont különböző növények növekedési szabályaival függenek össze.
A Penrose-csempézések, mint láttuk, ön-hasonlóak abban az értelemben, hogy ha felfújjuk vagy leeresztjük őket, akkor egy másik csempézést kapunk. A Fibonacci-sorozatok is rendelkeznek ugyanevvel a tulajdonsággal. Sokféle módon felfújhatók és leereszthetők úgy, hogy egy másik ilyen sorozatot kapjunk, de a legegyszerűbb a következő. A leeresztéshez cseréljünk ki minden R-et H-ra, minden HH-t R-re, és hagyjuk el az egyedül álló H-kat. Ha például a HRHHRHRHHRHHRHR sorozatot ezzel a szabállyal eresztjük le, akkor a leeresztettje HRHHRHRHH. A felfújáshoz cseréljünk ki minden H-t R re, minden R-t HH-ra, és két R közé mindenhova rakjunk be egy H-t.
Egy Fibonacci-sorozatban sosem fordulhat elő RR vagy HHH. Ezt felhasználva könnyen eldönthető, hogy R-ek és H-k egy sorozata Fibonacci-e. Alkalmazzuk a leeresztési szabályt egészen addig, míg vagy egy olyan sorozatot nem kapunk, amelyben RR vagy HHH van (ebben az esetben a sorozat nem Fibonacci), vagy egyetlen betűt nem kapunk, ami bizonyítja, hogy az. Egy Penrose-csempézés felfújásakor vagy leeresztésekor az Ammann-csíkok bármelyik családjához tartozó sorozat is felfújódik, illetve leeresztődik. Bármelyik olyan hernyóban, mint a kocsikerékminta tíz küllőjének hernyói, a hosszú és rövid csokornyakkendők sorozata szintén Fibonacci-sorozat.
Az Ammann-csíkok két családja nem periodikus paralelogrammák olyan hálózatát hozza létre, melybe beleilleszkednek a csempék. Ahogy Grünbaum és Shephard fogalmazza, "az, ami alapvető, az a csíkok rendszere, és a csempék szerepe mindössze az, hogy egy gyakorlati megvalósítást adnak". A csíkok valami olyasmik, amik halványan emlékeztetnek a kvantummezőkre, melyek meghatározzák a részecskék helyét és pályáját. Ammann volt az első, aki már 1977 elején észrevette, hogy a csíkok hálózata "kényszertételek"-hez vezet – olyan tételekhez, melyek arról szólnak, hogy csempék egy kicsiny halmaza hogyan határozza meg végtelen sok más csempe helyzetét.
Ammann felfedezéseiből kiindulva Conway számos további figyelemre méltó kényszertételt mondott ki. Most csak azt említem meg, miszerint két Penrose-csempe (mindkettő akármilyen típusú lehet), ha megfelelően helyezzük el őket, tetszőleges távolságra egymástól, csíkok két végtelen (nem teljes) családját határozza meg. Az egymást metsző két egyenescsalád viszont végtelen sok csempe helyzetét határozza meg. A király, dáma, bubi, kettes és a csillag például olyanok, hogy birodalmukban végtelen sok csempe helyét kényszerítik ki.
Aranyszögnek nevezik azt a szöget, melynek koszinusza az aranymetszés hányadosa:
cos![]() = 0,618034...
= 0,618034...
E szög értéke a függvénytáblázat alapján
![]() = 51°49’43”
= 51°49’43”
Az aranyszög körzővel és vonalzóval
való szerkesztése visszavezethető az aranymetszet euklideszi szerkesztésére.
Legyen r és R az O középpontú koncentrikus körök sugarai
és legyen az r az R sugarú szakasz nagyobbik aranymetszete.
Az AB húr legyen az r sugarú kör érintője, és C legyen
az érintési pont. Ekkor az OAC derékszögű háromszögben az AB
húr fele, ![]() és
és ![]() .
.
Ismeretes, hogy az aranymetszési
hányadosra fennáll a ![]() összefüggés.
összefüggés. ![]() helyébe
helyébe ![]() -t írva, az
-t írva, az
![]()
egyenletet kapjuk. Mivel ![]() az egyenlet mindkét oldalát
az egyenlet mindkét oldalát ![]() -val szorozva, a
-val szorozva, a
![]()
egyenlethez jutunk. A ![]() azonosság felhasználásával a
azonosság felhasználásával a ![]() alakot , majd mindkét oldalt
alakot , majd mindkét oldalt ![]() –val osztva (
–val osztva (![]() ),
),
![]()
összefüggést kapjuk, ahol
![]() . Az egyenlet geometriai jelentése, hogy a belső körhöz annak C pontjában
húzott CA érintőszakasz megegyezik a külső kör D pontbeli érintőjének
az érintési pont és a szög szára közötti
DE szakaszával.
. Az egyenlet geometriai jelentése, hogy a belső körhöz annak C pontjában
húzott CA érintőszakasz megegyezik a külső kör D pontbeli érintőjének
az érintési pont és a szög szára közötti
DE szakaszával.
Az aranyszög számos díszítő alakzaton felfedezhető. A középkor építészei, művészei az arány isteni eredetének megfelelően az aranymetszésnek és az aranyszögnek különös jelentőséget tulajdonítottak. Azok a szimbólumok, jelképek, melyek az Ég és a Föld viszonyára vonatkoznak, az aranymetszési arány hordozói.
Az aranyszöggel számos egyéb, jelképet hordozó relikvián, emléken találkozunk. Aranyszöget zárnak be az ismert Krisztus-monogram X jelének szárai a P betű szárával, és aranyszöget fedezhetünk fel Szent István királyunk REX ST (Rex Stephanus) betűjeleket tartalmazó ligatúrás kézjegyén is

Esett már szó az aranyháromszögről, mely azért különleges
háromszög, mert oldalainak aránya az aranymetszés arányával egyezik meg. Négyszögek
közt is létezik ilyen hasonló tulajdonságokkal rendelkező síkidom. Ezt aranytéglalapnak
nevezünk, mert oldalainak aránya éppen az aranymetszés aránya,![]() . Magában az a tény, hogy létezik, még nem bírna olyan nagy jelentőséggel,
viszont – ahogyan az aranyháromszög esetében is láttuk – az aranytéglalap
is sok érdekességet rejt magában. Hogy mit, arról picit később lesz szó.
. Magában az a tény, hogy létezik, még nem bírna olyan nagy jelentőséggel,
viszont – ahogyan az aranyháromszög esetében is láttuk – az aranytéglalap
is sok érdekességet rejt magában. Hogy mit, arról picit később lesz szó.
Először néhány szót arról, hogyan szerkeszthető az aranytéglalap.
Már az aranymetszés és az ötszög esetében láttuk, hogy nem is olyan egyszerű
megszerkeszteni két egymással ![]() arányban lévő szakaszt. Azonban mégsem olyan ördöngős feladatról van szó.
Az aranymetszés utolsó konstrukciójának alapján fogunk eljárni.
arányban lévő szakaszt. Azonban mégsem olyan ördöngős feladatról van szó.
Az aranymetszés utolsó konstrukciójának alapján fogunk eljárni.
Legyen adott egy a oldalú ABCD négyzet. AB illetve CD oldalak M illetve N felezőpontjait összekötve C illetve D csúcsokkal két egyenlő hosszúságú MC illetve NB szakaszokat kapunk. Ezekkel a sugarakkal a két felezőpontból, M-ből és N-ből metszve [AB) és [DC) félegyeneseket kapjuk E illetve F metszéspontokat, és így eljutunk AEFD téglalaphoz.
Mivel ![]() és
és ![]() , ezért
, ezért ![]() olyan derékszögű háromszög, melynek átfogója
olyan derékszögű háromszög, melynek átfogója ![]() . Mivel
. Mivel ![]() és
és ![]() , ezért
, ezért
![]() ,
,
tehát a szerkesztett téglalap oldalainak aránya ![]() , vagyis AEFD aranytéglalap.
, vagyis AEFD aranytéglalap.
Hogy miért is kellett megemlíteni az aranytéglalapot, a következő részből kiderül.
[1] Brassai Sámuel 1896-ban megjelent fordítása
[2] Brassai Sámuel 1896-ban megjelent fordítása
[3] Brassai Sámuel 1896-ban megjelent fordítása
[4] Brassai Sámuel 1896-ban megjelent fordításából
[5] A tétel bizonyítása megtalálható Hajós György: Bevezetés a geometriába c. könyvének 22.§-ában.
[6] A tétel bizonyítása megtalálható Hajós György: Bevezetés a geometriába c. könyvének 22.§-ában.