Az aranymetszés térgeometriája

Aranymetszés a platonikus testekben
Térkitöltés - Arany romboéderek és kvázi-kristályok

Aranymetszés a platonikus testekben

Platonikus testeknek nevezzük a szabályos testeket, azokat a konvex poliédereket, melyeknek élei, élszögei és lapszögei egyenlők. Az élek és élszögek egyenlőségéből következik, hogy a szabályos test lapjai egybevágó szabályos sokszögek, lapjai tehát mindennyian ugyanannyi oldalúak. Az élszögek és a lapszögek egyenlőségéből következik, hogy a szabályos testszögletei egybevágó szabályos szögletek, tehát ugyanannyi élűek.

Könnyen igazolható, hogy összesen öt ilyen test létezik. Ezek lapszám szerinti sorrendben a tetraéder, a hexaéder, az oktaéder, a dodekaéder és az ikozaéder, melyek közül az utóbbi három vizsgálható az aranymetszés szempontjából.

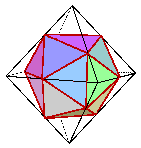
Legkülönlegesebb kapcsolat az ikoza- és az oktaéder között figyelhető meg. Az oktaéder egy ikozaédert rejt magában oly módon, hogyha az oktaéder éleinek aranymetsző pontjait összekötjük egy ikozaédert kapunk eredményül.

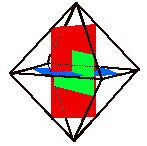
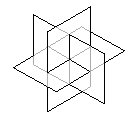
Hogy hogyan lehetséges ez, egyből előtűnik, ha a két test „vázát” vesszük szemügyre. És itt lép színre a már korábban említett aranytéglalap. Ha három aranytéglalapot speciális helyzetbe állítunk, azaz egymásra merőleges és egymást metsző helyzetbe hozunk, a kapott „kereszt” éppen egy ikozaédert eredményez.

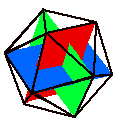
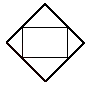
Ebből a „vázból” pedig úgy jutunk el az oktaéder „vázáig”, hogy a téglalapokat négyzetekké egészítjük ki. Az aranytéglalap és a köré írható négyzet úgy helyezkednek el egymáshoz képest, hogy a négyzet oldalainak megfelelő aranymetsző pontjai határozzák meg a téglalap csúcspontjait. Ebből a tényből, valamint abból, hogy a három egymást metsző négyzet egy oktaédert határoz meg, egyértelműen következik, hogy az oktaéder éleinek aranymetsző pontjai egy ikozaéder csúcspontjai lesznek.

De vajon mi köze mindehhez a dodekaédernek? Ez a „triumvirátus” benne is megtalálható, csak még jobban elrejtve.

A dodekaéder és az ikozaéder között egy különleges kapcsolat van. Ez a két test egymásnak duálisa, ami azt jelenti, hogy az egyik lapközéppontjai a másik csúcspontjait határozzák meg. Tehát az ikozaéder csúcspontjai egy dodekaéder lapközéppontjait határozzák meg, ami azt jelenti, hogy a három aranytéglalap csúcsai ezúttal egy dodekaéder lapközéppontjaival egyeznek meg:

Térkitöltés – Arany romboéderek és kvázi-kristályok

Penrose megtalálta a megoldást a sík teljes lefedésére két olyan egyszerű alakzat segítségével, amelyek ötszörös forgásszimmetriát mutatnak. Ez a felfedezés nagy jelentőséggel bírt, mert korábban úgy vélték, nem létezhet ilyen. Hasonlóan vélekedtek a tér hézagmentes kitöltéséről is, de Penrose eredményei megingatták ezt a dogmát.

Ammann másik nagy felfedezése, szintén 1976-ból, egy két romboéderből (olyan paralelepipedon, melynek hat egy bevágó rombuszlapja van) álló készlet volt, mellyel alkalmas illesztési szabályok esetén csaknem periodikusan csempézhető a tér. A két romboéder testhálója:

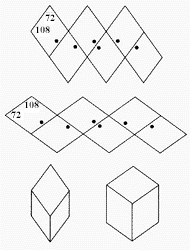
Ha kartonpapírból kivágjuk a két hálót, a vonalak mentén összehajtva és az éleket összeragasztva megkapjuk az ábra alsó részén látható két testet. Az egyik olyan, mint egy testátlója mentén összenyomott, a másik pedig, mint egy testátlója mentén széthúzott kocka. Mind a tizenkét lap egybevágó, a lapátlók aránya aranymetszés. H. S. M. Coxeter, a híres geométer, az ilyen típusú romboédereket "arany romboéder"-nek nevezte. Mindössze kétféle arany romboéder van, melyek mindegyikét tanulmányozta már Kepler is. A hegyes szögű arany romboédernek van két átellenes csúcsa, melyben három egyenlő hegyesszög találkozik. A tompaszögű arany romboédernek olyan két átellenes csúcsa van, melyben egyenlő tompaszögek találkoznak. Mindkét test több csúcsában vegyesen fordulnak elő hegyes- és tompaszögek.

Ammann két romboédere éppen a kétféle arany típusú. A periodikus csempézést megfelelően elhelyezett lyukakkal és kiemelkedésekkel akadályozhatjuk meg. Figyeljük meg az ábra testhálóin a pöttyöket. Képzeljük el, hogy mindkét testnek elkészítjük a másolatát úgy, hogy a pöttyök mintázata a tükörképe legyen az eredetiének. Ekkor egy olyan, négy testből álló készletet kapunk, mellyel csaknem periodikusan lehet csempézni, ha úgy illesztjük össze a darabokat, hogy minden pötty fedjen egy másik pöttyöt. Nem tudni, hogy ez a tükrözés kihagyható-e úgy, hogy csak két – megfelelő jelölésekkel ellátott – test kényszerítse ki a nem periodikus csempézést. Ha egy sík megfelelő szögben metszi a kicsempézett teret, akkor a síkon a Penrose-rombuszokéhoz nagyon hasonló csempézés jelenik meg.

Egy évvel a tér Ammann-féle nem periodikus csempézésének felfedezése után a japán Koji Miyazaki, a kobei egyetem építésze újra felfedezte azt. Ezen kívül talált egy másik módot is arra, hogy a két arany romboéderrel nem periodikusan csempézzük a teret, bár ez a csempézés nem kikényszerített. Öt hegyesszögű és öt tompaszögű arany romboéder illeszkedik úgy össze, hogy egy rombikus triakontraédert alkotnak. Két ilyen testet, melyek hegyesszögű csúcsukban érintkeznek, körülvehetünk további hatvan arany romboéderrel (mindkét típusból 30) úgy, hogy egy nagyobb rombikus triakontraédert kapjunk. Ez a nagyítás a végtelenségig folytatható, méhsejtszerűen csempézve a teret, melynek közepe ikozaéderes szimmetriát mutat.

Penrose 1976 májusában a következőket írta Gardnernek:

„Még az is lehetséges, hogy ezek a dolgok jelentőséggel bírhatnak a biológia szempontjából. Ne felejtsük el, hogy bizonyos vírusok szabályos dodekaéder és ikozaéder alakban növekednek. Mindig is zavarba ejtő kérdés volt, hogy hogyan csinálják ezt. Ammann nem periodikus testeivel viszont mint alapegységekkel, kváziperiodikus "kristályokhoz" juthatunk, olyan látszólag lehetetlen (kristálytanilag) hasadási irányokkal, melyek síkjai dodekaédert vagy ikozaédert határoznak meg. Lehetséges, hogy talán a vírusok növekedése is valami ilyesfajta nem periodikus egységen alapul –- vagy túlságosan elrugaszkodott ez az elképzelés?”

Penrose sejtései a kristályokról még megfogalmazásukat tekintve is meglepően profetikusnak bizonyultak. Az 1980-as évek elején számos természettudós és matematikus kezdte fontolóra venni annak lehetőségét, hogy kristályok atomi szerkezete esetleg alapulhat egy nem periodikus hálózaton is. Ezt követően 1984-ben Dany Schechtman és kollégái a Nemzeti Szabványügyi Hivatalnál drámai bejelentéssel álltak elő. Nem periodikus szerkezetet találtak egy hirtelen lehűtött alumínium-mangán ötvözetnek – melyet a kémikusok azonnal elneveztek Schechtmanitnak – az elektronmikroszkópos vizsgálata során. A mikroszkóp világosan mutatta az ötszöges szimmetriát, ami erősen sugall egy a Penrose-csempézéssel analóg nem periodikus csempemintát a térben.

Semmi ehhez hasonlót nem tapasztaltak korábban, ahogy Ivars Peterson szakíró megfogalmazta, ez olyan volt, mintha valaki egy ötszögű hópelyhet figyelt volna meg. A krisztallográfiában régóta egyfajta dogmának számított, hogy a kristályok csak 2, 3, 4 vagy 6-szoros forgásszimmetriával rendelkezhetnek, 5, 7 vagy 8-szorossal soha. Egy másik dogma szerint a szilárd anyagok szerkezete csak kétféle lehet, az atomok elrendezése vagy periodikus, vagy teljesen rendezetlen, mint az üveghez hasonló amorf anyagokban.

A rendezett szerkezetű kristályok közül minden ismert kristályhálót három szabályos platóni testre – tetraéder, kocka, oktaéder – vezettek vissza. A dodekaédert és az ikozaédert azért zárták ki, mert ötszörös szimmetriájuk lehetetlenné tette a periodikus csempézést. És akkor itt volt egy anyag, amely úgy tűnt, hogy ikozaéderes szimmetriát mutat. Akárcsak a Penrose-csempézés 72 fokkal, azaz a teljes kör ötödrészével elforgatva nagyjából – egy általános statisztikai értelemben – változatlan maradt, de hosszú távú periodicitás nélkül. Úgy tűnt, hogy a szerkezete valahol félúton van az üveg és a rendezett kristályok között, azt mutatva, hogy a kétféle szerkezet közti éles határ helyett átmeneti formák folytonos sokasága lehetséges.

A fizikusok, kémikusok és krisztallográfusok körében ez a felfedezés a robbanás erejével hatott. Hasonló, nem periodikus szerkezeteket fedeztek fel hamarosan más ötvözetekben, és cikkek tucatjai kezdtek megjelenni. Világossá vált, hogy szilárd anyagok nem periodikus rácsszerkezete bármiféle forgásszimmetriát mutathat. Két vagy több csempéből álló térbeli készletek széles választékát adták meg modellként, melyek némelyike kikényszeríti a nem periodikus csempézést, némelyike pusztán lehetővé teszi. Előállítottak egy réteges kristályszerkezetet, melynek egymáson fekvő rétegei a Penrose-féle síkbeli rombuszos csempemintát mutatják. A holland N. G. de Bruijn kifejlesztette a nem periodikus csempézés algebrai elméletét, amely az Ammann-csíkokhoz hasonló, általa "pentarácsok"-nak nevezett szerkezeteken alapul. Egy 1987-es publikálatlan cikkben meglepő kapcsolatról számolt be a nem periodikus csempézések elmélete és egy kártyakeverési tétel – melyet a bűvészek Galbreath-féle elv néven ismernek – között.

Mindezek igen megtermékenyítően hatottak a "kvázi-kristályok" – ahogy most ezeket az új, félúton levő kristályokat nevezik – kísérleti és elméleti kutatására. Ugyanakkor ellenzői is vannak annak a nézetnek, hogy ezek a rácsszerkezetek természetükből adódóan nem periodikusak. Az ellenzők vezéralakja Linus Pauling, aki szerint a mikroszkópos képet úgy kellene magyarázni, hogy az ötszörös szimmetria hamis formáját mutatja, melyet a krisztallográfusok sokszoros ikerképződésként ismernek. "Nem kell tovább aggódniuk a krisztallográfusoknak amiatt, hogy tudományuk egyik elfogadott alappillérének érvényessége megkérdőjeleződött" – jelentette ki Pauling a Nature egy 1985-ös cikkében. Egy másik lehetőség, hogy a kvázi-kristályok egyszerűen csak hatalmas egységcellái egy periodikus mintának, ami ki fog derülni, mihelyt nagyobb mintákat készítenek. És vannak más lehetőségek is. A kvázi-kristályok hívei azt állítják, hogy mindezeket az alternatív magyarázatokat kizárták, és a nem periodikus minta a legegyszerűbb magyarázat. Lehet, hogy néhány éven belül a kísérleti kutatások megcáfolják, és a kvázi-kristályok a balsorsú polivíz sorsára jutnak; de ha a nem periodikus magyarázat igaznak bizonyul, akkor az szenzációs fordulópont lesz a krisztallográfiában.

Feltéve, hogy a kvázi-kristályok tényleg léteznek, a következő néhány évben várhatóan egyre hatékonyabb technikák fognak megszületni az előállításukra. Sok kérdés vár válaszra. Miféle fizikai erők játszanak szerepet az ilyen furcsa kristályok képződésében? Milyenek a rugalmassági és elektromos tulajdonságai a kvázi-kristályoknak? Fognak-e a geológusok valaha is természetes módon képződött kvázikristályt találni?

Ha a kvázi-kristályok olyanok, mint amilyennek hívei hiszik õket, akkor kitűnő példát szolgáltatnak arra, hogy hogyan derülhet ki valamiről, amit a népszerű matematika pusztán a szórakozás és az esztétikai élvezet kedvéért hozott létre, hogy a fizikai világban és a technológiában jelentős gyakorlati alkalmazásai vannak.