

Ez az egyike annak a három szimmetrikus alakzatnak, amelybõl a "Boy-felület" poligonális reprezentációja felépülhet. Ez a darab egy lóhere (cloverleaf) alakú formából áll, amely egy gyûrû alakú hengeres alakzatot fed be. A lóhere maga egy kör ¾ -ébõl áll, amihez egy szögletes negyedik negyed kapcsolódik. A lóhere elõállítható egy egyenes szakasz, egy kör ¾-e, majd egy másik egyenes szakasz segítségével, így formálva egy gyûrûs alakzatot. Ennek eredményeképp egy újabb üres lóhere terület keletkezik a gyûrûs alakzat közepén. Ez a terület egyike azon két helynek, ahol a szimmetrikus részek kapcsolódhatnak egymáshoz. A fenti alakzat nem teljes két ok miatt: elõször is a középen lévõ lóherés résznek záródnia kell, hogy valódi Boy-féle felület legyen; másodszor pedig a gyûrûs alakzat egyik vége keresztül fog menni a másik kettõ egy-egy végén, ahelyett hogy egy olyan határt alkotna, ahol a három darab találkozik.
Többféle megoldás létezik, hogy a befedjük a belsõ üres lóherés részt, megoldva ezzel az elsõ problémát. Megoldható, hogy az összes paramétervonal egy pontban találkozzon, mint a következõ alakzatban:

Egy alternatív megoldással a felületet négyszöghálóval is be lehet fedni:

Két gyûrûs darabot összeillesztve kapjuk a következõ formát:

Ezen az alakzaton megfigyelhetõ a két kapcsolódás amely a gyûrûszeletek között áll fenn. Az egyik szelet vége a másikat középen érinti, miközben a másik két vég találkozik és metszi egymást egy másik helyen.
Végül itt van a három gyûrûszelet együtt. Megfigyelhetõ a három gyûrûszelet egy helyen való (helytelen) metszése és a folytonos paramétervonalak is ahogy egyik szeletrõl a másikra haladunk.

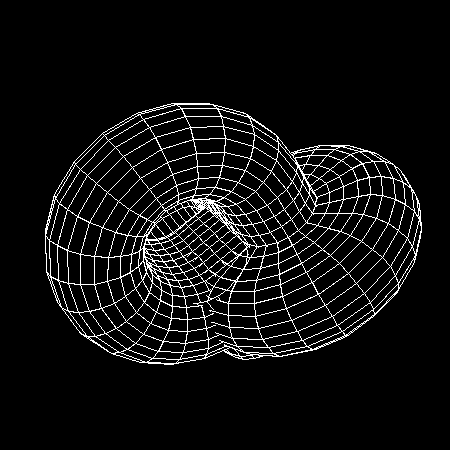

Nyilvánvalóan
az említett második probléma (a három gyûrûs
alakzat helytelen metszése) ezekkel a megjelenítésekkel
nem megoldható. Nem nehéz meghatározni egy olyan érintkezési
helyet ahol a három gyûrûszelet találkozik, de
olyat igen, amely sima és szép. Mivel a poligonális
megjelenítéssel a spline ábrázoláshoz
való alapokat akartuk megadni, amihez szükséges lenne
a spline érintkezések menti simasága; ez a bizonytalanság
nagyon zavaró volt.
Mivel ezzel a megközelítéssel nehéz lenne a simaságot biztosítani,még a poligonális megjelenítésnél is, Brakke programjának (Surface Evolver) használata jobb választásnak tûnt. A felületmegjelenítõ (Surface Evolver) sikeres használata által egyenletes poligonális és drótvázas megjelenítéseket kaptuk a következõ részben leírtak szerint.
Mivel az Evolver ki tudja simítani a háromszögeléseket, a Boy féle felületnek csak egy nagyon nyers modelljét kellett kiindulási pontnak venni. A kiindulási modell 54 felületbõl állt és Carlo Sequen megszerkesztette körültekintõen úgy, hogy a csúcsok csak 5, 6, 7 valenciával rendelkezzenek. Mivel az Evolver közelítõ eljárással a háromszögeket oldalfelezõ pontjaik összekötésével osztja fel, az összes újonnan létrejövõ csúcs 6 valenciás lesz. A következõ ábra megmutatja a Boy féle felület kezdeti nyers modelljét:

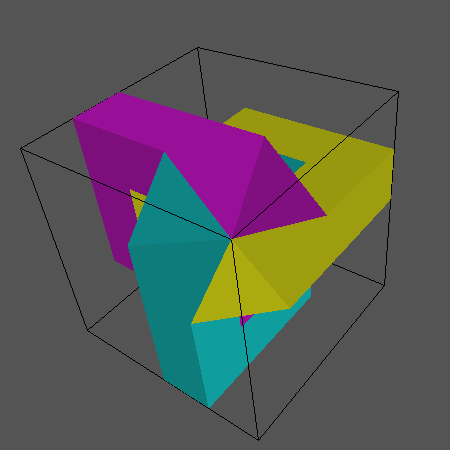
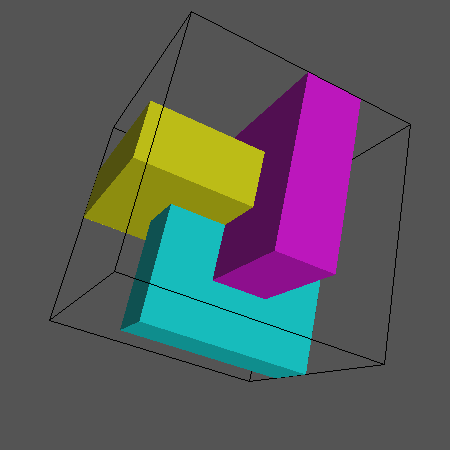

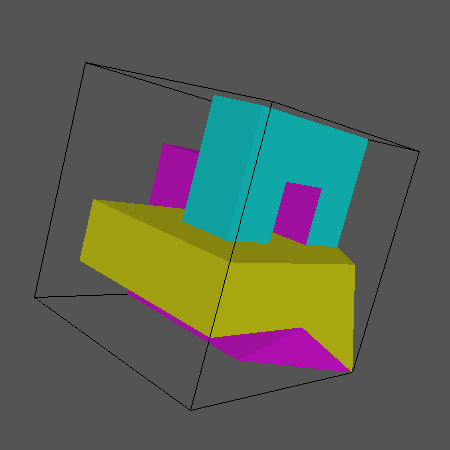
Figyeljük meg, hogy itt a tényleges gyûrûszeletek helyett U alakú szeletek vannak, melyek találkoznak és egy pontot alkotnak.
Ezen modellbõl kiindulva, eleinte tisztázatlan volt, vajon képes lesz e az Evolver a szükséges sima felületet kialakítani. Az elsõ futtatások alatt az Evolver jó munkát végzett az éles tompaszögû lapszögek kisimításánál, de meglehetõsen hatástalannak mutatkozott az éles szögletek simításánál. Sok kísérletezés után felfedeztem, hogy a finomítás megfelelõ szintjén a csúcs közepelés módszerével és a görbület minimalizáció megfelelõ beállításával az éles szögletek kisimíthatóak. Ezekkel a beállításokkal képes voltam a következõ sima felületet létreho zni 858 háromszög segítségével.
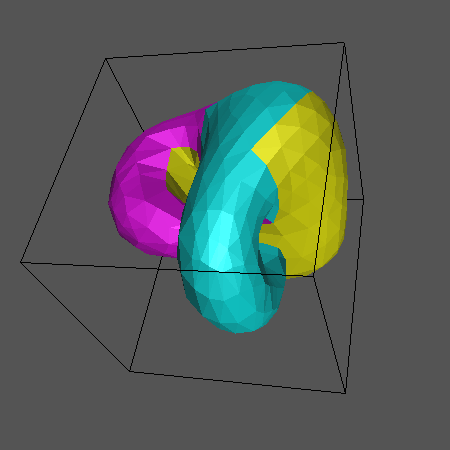
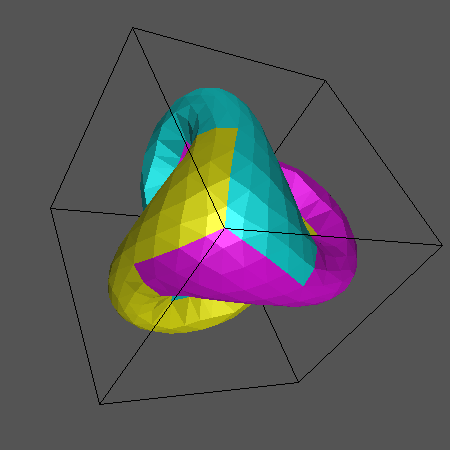

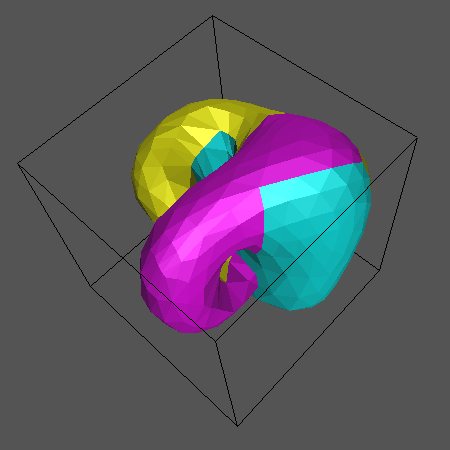
Evolver Drótvázas modell
Mivel az Evolvert már beállítottam, hogy sima felületet készít sen, lehetõség nyílt arra, hogy drótvázas felületet lehessen belõle kialakítani. A drótvázas felület az általam elkészített háromszögháló duálisa, azzal a különbséggel, hogy tartó éleket (struts) megvastagítjuk és nem töltjük ki a felületét.
A következõ a lakzatok úgy készültek, hogy fogtuk az Evolverrel készült felületet és összekötöttük a háromszög középpontjait paralelepipedonokkal .


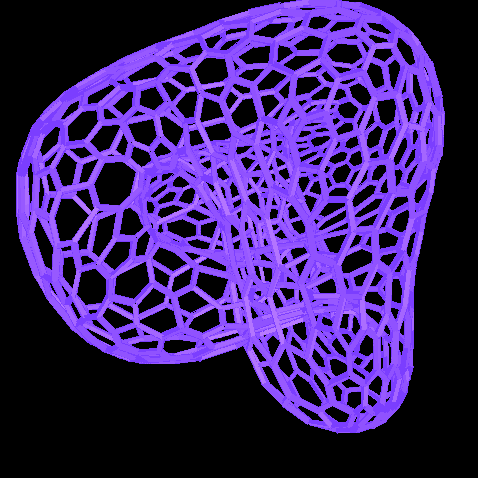



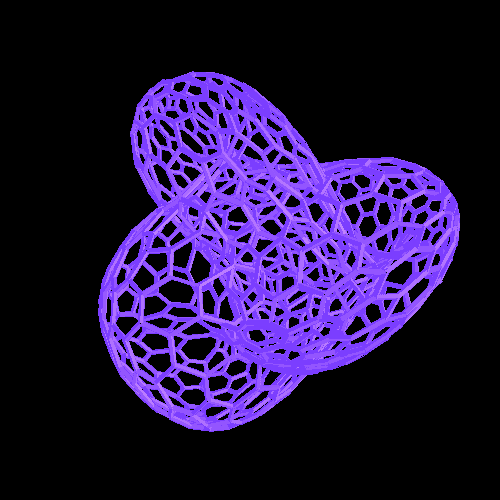


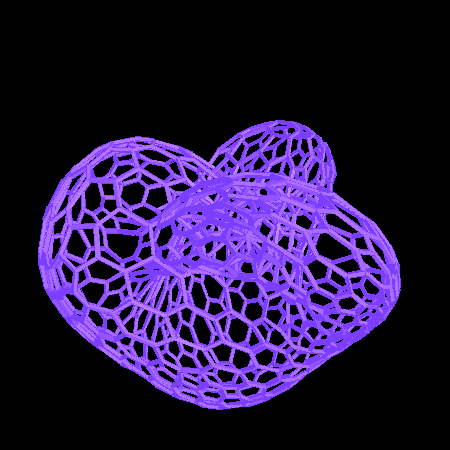
Miközben a fenti megközelítés láthatóság szempontjából megfelelõ, van két lényeges probléma, amelyet meg kell említenünk. Az elsõ, hogy a paralelepipedonok egyszerûen elmetszik a háromszögcsúcsokat, ahelyett, hogy valódi felületet alkotnának. A második az, hogy a tartó éleknek vannak olyan metszései ahol a felszín különbözõ részei keresztezik egymást . A teljes láthatóság érdekében azt szeretnénk, hogy a drótváz modell a felület különbözõ részein független legyen.
Egyfajta megoldás az elsõ problémára, hogy minden háromszög közepére egy háromszög alapú prizmát teszünk és összekötjük a paralelepipedonokat a négyszögletes hasábokkal. Ez a megközelítés zárt felületet hoz létre, de a tartók között különbözõ távolságokat eredményezhet, a lapszögektõl és a szom szédos háromszögek egymáshoz képest lévõ fekvésétõl függõen. Ezt a megoldást már megvalósították, de még mindig ellenõrzés alatt van.
A probléma jobb megoldásai megtalálhatnák a paralelepipedonok egymással való adott metszéseit a csúcsoknál és ezeknél a metszéseknél elvágnák, majd az összes üresen maradt részt megtöltenék. Az is egy (kicsit könnyebb) lehetõség, hogy egy kockát vagy más testet helyeznénk minden háromszög közepébe, ezzel mintegy lefedve a paralelepipedonok metszéspontjait, vagy gondoskodná nk egy egyszerûbb geometriáról amelyikkel kiszámolhatnánk a paralelepipedonok metszéseit. Ez, természetesen, megkövetelné a tárgy drótvázas végsõ megjelenítését. Jóllehet könnyû kézzel irányítani a háromszögek közepeinek helyét , hogy igy oldjuk meg a máso dik problémát, egy algoritmikus megoldás meglehetõsen nehéz. Sajnos nem volt idõm, hogy ezzel kapcsolatban kutatásokat végezzek, de itt van néhány lehetséges megoldás: olyan program írása, ami kimutatja a tartó élek ( metszéseit és mozgatni tudja a háromsz ögek középpontjait, vagy visszatéve a drótvázat az Evolverbe és így megpróbálni a tartó éleket eltolni egy mástól.
Befejezés és jövõbeni tervek
Négy hét munka után. Amit ennek a projectnek a kidolgozásával töltöttem arra a következtetésre jutotta, hogy a Boy féle felület ábrázolása nem könnyû feladat. Ez a nehézség leginkább annak a ténynek köszönhetõ, hogy habár a Boy féle felület a projektív sík modellje, nincsen kézzel fogható szimmetrikus u,v paraméterezése. Ésszerû paraméterezés nélkül úgy tûnik, hogy nehéz poligonokat vagy splineokat a felületre helyezni ugyanakkor elkerülni az olyan helyzeteket, ahol érdekes dolgok történnek (például paramétervonalak eltûnése).
Van még néhány lehetséges út ( jövõbeni feladatként) a Boy féle felület ábrázolásához. Egyik ezek közül egy hatszögletû terület leképezése a felületre, mely lehetõség szerint három négyoldalú síkidomra bontja a hatszögletû területet. Ez a poligonális és spline megjelenítésekhez szükséges lehetséges paraméterezést. Adhatna. Egy másfajta megközelítéssel egy szimmetriára alapozott poligonális paraméterezés lehetne, ami ha lehetséges- elkerülné a furcsa pontokat
A jelenlegi munkám függvényében,
a célom, hogy befejezzem a háromszögletû prizmás
eljárást az élek összekötéséhez
és az eredményül kapott STL-t , ami fe ldolgozható
SFF eljárással. A résznek még mindig lesznek
metsz? tartói , tehát ezért nem lehet SFF folyamattal
átalakítani. Számításaim szerint a merev
metszések elkerülésének megoldása idõbe
fog telni, ezért a befejezés még várat magára
a közeljövõben.
És végül néhány érdekes kép: