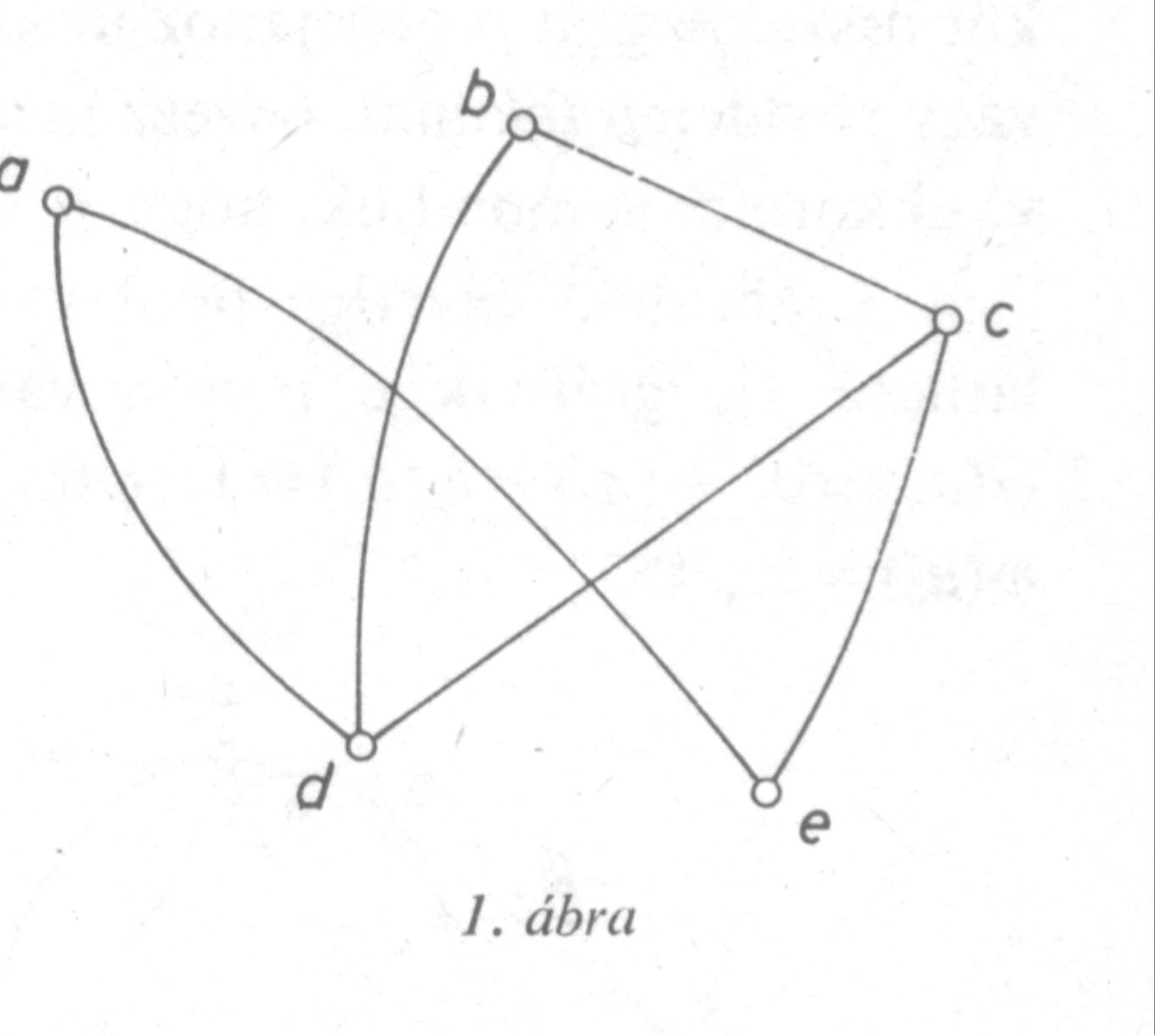
Mi a gráf? Tekintsük pl. egy n csapatból álló labdarúgó bajnokság állását. A már lejátszott és még le nem játszott mérkőzésekről szeretnénk áttekinthető képet kapni. Jelöljük a csapatokat körökkel (és írjunk melléjük egy betűt vagy egy számot-ezek azonosítják a csapatokat). Ha két csapat már játszott egymással, akkor kössük össze az őket jelképező pontokat egy vonallal. Amennyiben azt is szeretnénk ábrázolni, hogy két csapat közül melyik volt a vendég, akkor lássuk el egy nyíllal az őket összekötő vonalat (pl. a nyíl mutasson a vendégtől a hazai csapat felé). Az így kapott, pontokból és vonalakból álló ábrát gráfnak nevezzük. A köröket a gráf pontjainak, a köröket összekötő vonalakat a gráf éleinek nevezzük.

A gráf egy adott pontjából kiinduló élek számát a pont fokszámának nevezzük. Az 1. ábrán például grad(d)=3, grad(b)=2. Ha a gráfban van két olyan pont, amelyet több él is összeköt, akkor azt mondjuk, hogy a gráf tartalmaz többszörös éleket. Ha egy gráfban az “a” pontból úgy jutunk el egy “b” pontba, hogy közben bármely pontot legfeljebb egyszer érintünk, akkor azt mondjuk, hogy úton haladtunk. Az 1. ábrán ilyen út például az a-d-c-b vagy a-d-b vagy a-e-c-b. Ha egy út kezdő és végpontja azonos, akkor körről beszélünk (a fenti ábrán például a-d-c-e-a vagy d-c-b-d egy-egy kör). Egy út vagy kör hosszán éleinek számát értjük. Az olyan élt, amelynek mindkét vége ugyanaz a pont, hurokélnek nevezzük. Egy gráfban két pontot szomszédosnak nevezünk, ha él köti össze őket. Két élt szomszédosnak nevezünk, ha egyik végpontjuk közös. A 2. ábrán például b2 és b3 valamint b1 és b5 szomszédos pontok, ugyanakkor f6 és f9 valamint f3 és f4 szomszédos élek.
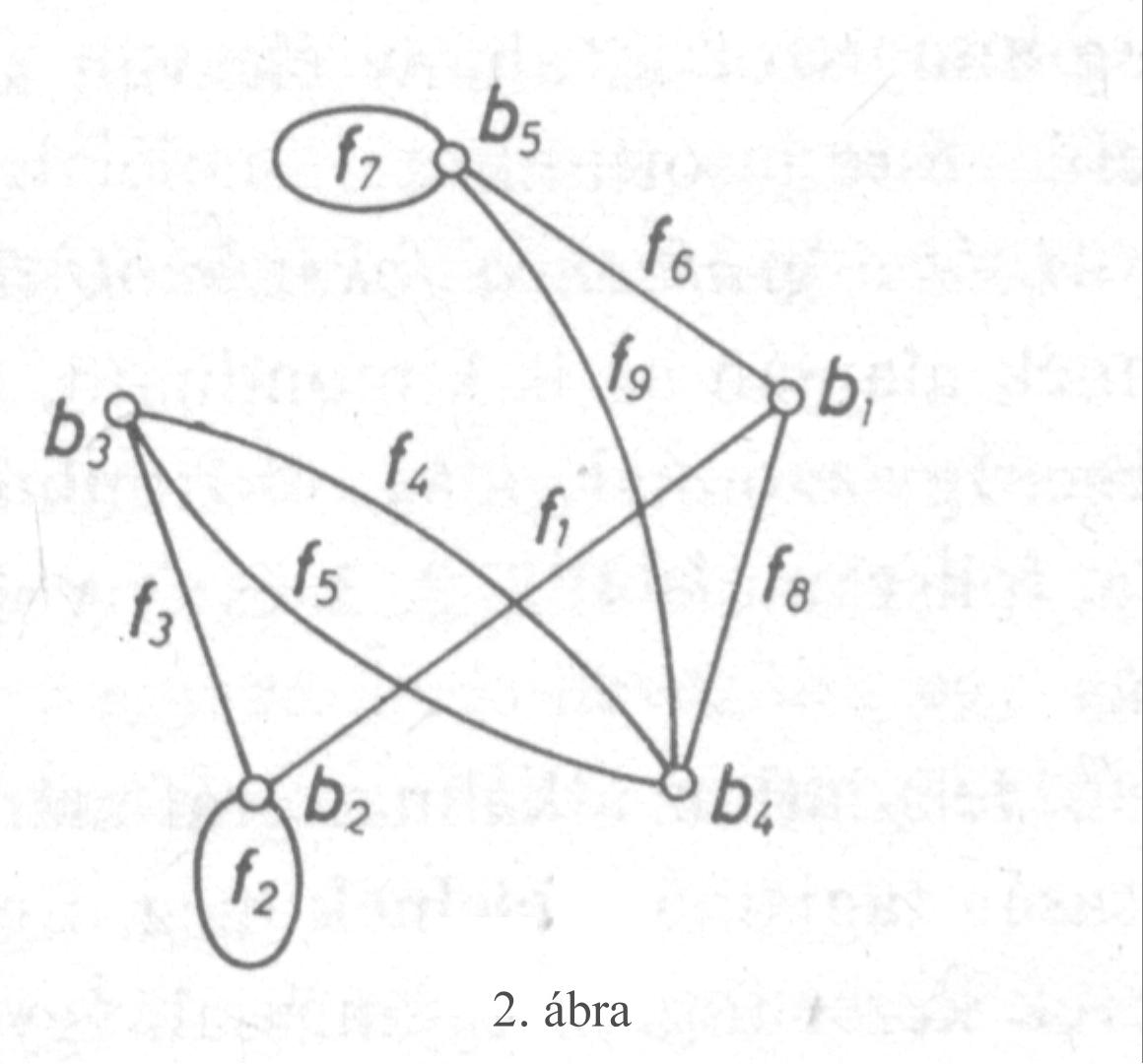
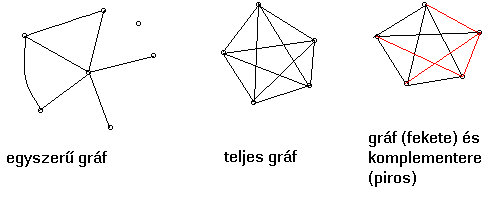
A 2. ábrán hurokél az f2 illetve f7. Ugyanakkor többszörös él például a b3 és b4 pontokat összekötő f4 és f5 élek. Egy gráfot egyszerűnek nevezünk, ha sem hurokélt, sem pedig többszörös éleket nem tartalmaz. Az olyan egyszerű gráfot, amelyben bármely két különböző pontot egy és csak egy él köt össze, teljes gráfnak nevezzük. Ha egy gráfban bármely két pont úttal elérhető, akkor a gráfot összefüggőnek nevezzük. Egy gráf komplementerén azt a gráfot értjük, amelynek az eredeti gráffal való egyesítése teljes gráfot ad.
Ha egy gráf bizonyos éleit és/vagy pontjait - a pontokat a hozzá illeszkedő élekkel együtt - töröljük, akkor ismét egy gráfot kapunk. Az így kapott gráfot az eredeti gráf részgráfjának nevezzük. A G gráf azon részgráfját, amely nem azonos G-vel, a G gráf egy valódi részgráfjának nevezzük. A G gráf egy komponensén G egy olyan részgráfját értjük, amely összefüggő, de nem valódi részgráfja G egyetlen összefüggő részgráfjának sem.
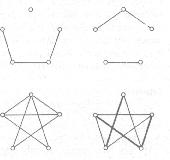
3/1. ábra komponensekről.
A 3/1. ábrán látható gráf 6 komponensből áll, ebből 4 darab van a felső sorban és 2 darab az alsó sorban.
A körmentes, összefüggő gráfot fagráfnak nevezzük. A 3/2. ábrán látható gráfok (6 darab gráf) mindegyike fagráf.
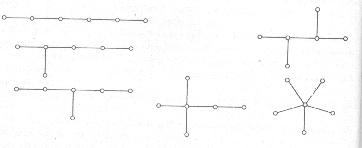
3/2. ábra
A gráfokat G betűvel (esetleg indexelve, ha többről van szó) jelöljük általában.
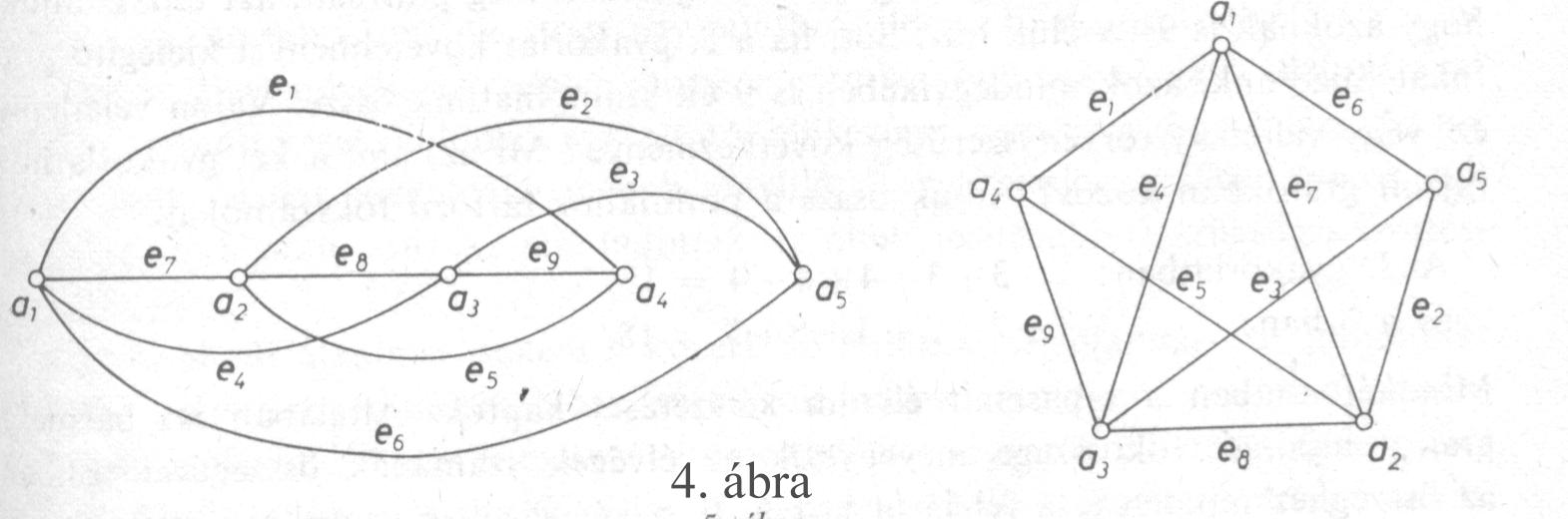
Két gráfot (G1 és G2) izomorfnak nevezünk, ha az egyik gráf pontjai és élei kölcsönösen egyértelműen és illeszkedéstartóan megfeleltethetők a másik gráf pontjainak illetve éleinek. A 4. ábrán látható két gráf izomorf.
1. tétel: Minden gráfban a fokszámok összege az élek számának kétszeresével egyenlő.
Bizonyítás: mivel minden él két pontot köt össze, ezért a fokszámok összege valóban az élek számának kétszeresével egyenlő.
2. tétel: Minden egyszerű gráfban a páratlan fokú pontok száma páros.
Bizonyítás: : mivel a pontok fokszámának összege egyenlő az élek számának kétszeresével, ezért ez a szám páros. Ha ebből az összegből levonjuk a páros fokú pontok fokszám összegét, a különbség továbbra is páros lesz. De ez a különbség éppen a páratlan fokú pontok fokszám összegével egyenlő. Ezzel beláttuk az állítást.
3. tétel: Az n-pontú teljes gráf éleinek száma n*(n-1)/2.
Bizonyítás: Vegyük a gráf egy tetszőleges pontját. Ebből n-1 darab él indul ki, mivel a gráf teljes. Mivel a gráfnak n pontja van, ezért első megközelítésben n*(n-1) él adódik. De ebben a meggondolásban minden élt pontosan kétszer veszünk számításba, így valójában az n-pontú teljes gráf éleinek a száma: n*(n-1)/2.
4. tétel: Ha egy gráfban minden pont foka legalább 2, akkor a gráfban van kör.
Bizonyítás: Induljunk el a szóban forgó gráf egy tetszőleges pontjából és haladjunk a gráf élein. Mivel minden pont foka legalább kettő, így bármelyik új pontba jutva, még be nem járt élen haladhatunk tovább. Csak akkor akadhatunk meg, ha már érintett pontba jutunk. Ekkor azonban a gráf egy körét is bejártuk. Ezzel beláttuk az állítást.
5. tétel: Ha egy n-pontú gráfnak legalább n éle van, akkor van a gráfban kör.
Bizonyítás: az állítást n-re vonatkozó teljes indukcióval bizonyítjuk. Az állítás n=1-re nyilván igaz. Tegyük fel, hogy valamely n>= 1-re minden n-pontú és legalább n-élű gráfban van kör. Belátjuk, hogy akkor minden n+1-pontú és legalább n+1-élű gráfban is van kör. Legyen G egy n+1-pontú gráf, amelynek legalább n+1 éle van. Ha G-nek van elsőfokú pontja, akkor töröljük ezt a pontot, a hozzá tartozó éllel együtt. Az így kapott gráfnak n pontja van és legalább n éle, így az indukciós feltevés szerint tartalmaz kört. Ezt a kört viszont G is tartalmazza. Ha G-nek nincsen elsőfokú pontja, akkor minden pontjának foka legalább 2, így a 4. tétel szerint van benne kör. Ezzel az állítást beláttuk.
Euler-vonalnak (illetve útnak) nevezünk a gráfban egy utat, ha a gráf minden élén pontosan egyszer halad keresztül.
Hamilton-körnek nevezzük a gráf egy olyan körét, amely a gráf minden pontján pontosan egyszer halad keresztül.
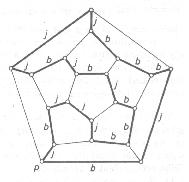
Rajzoljuk meg a tetraéder, a hexaéder, az oktaéder, az ikozaéder és a dodekaéder kiterített élvázának egy-egy Hamilton-körét! A dodekaéder esetén j (jobb) és b (bal) betűvel vannak jelölve az élek aszerint, hogy az élen haladva és egy csúcshoz érve, onnan balra vagy jobbra kell folytatni a bejárást. A gráf pontjainak bejárását a “p” pontból kezdjük. Egy ilyen bejárást a “bjbbbjjjbjbjbbbjjjbj” jelsorozattal lehet jellemezni.
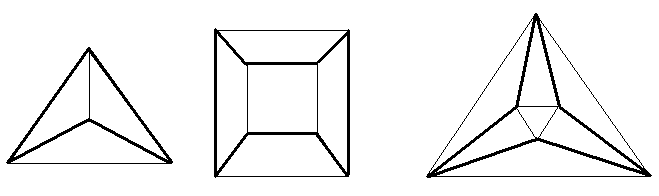
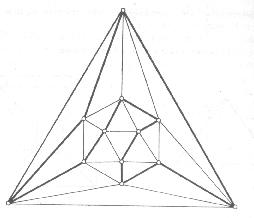
Feladat: mely szabályos
test élvázából készített gráfnak létezik Euler-köre? Amelyiknél létezik
Euler-kör, annál rajzoljunk is meg egyet!
vissza a főmenübe!