Tekintsük az alábbi feladatokat:
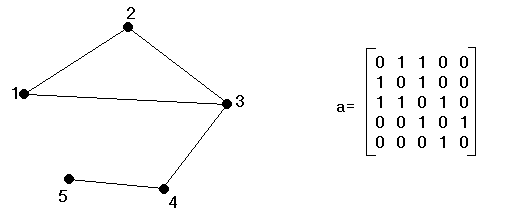
Ha a gráfot számítógépben tároljuk, akkor persze nem vihetjük be a gráf rajzát a gépbe. Ehelyett megszámozzuk a gráf pontjait az 1, 2, 3, ...,n számokkal és egy n*n-es mátrixot képezünk, melyben aij =1, ha az i-edik és j-edik pont össze van kötve és aij=0, ha nincsenek összekötve.
Ezt a mátrixot a gráf adjacencia-mátrixának (szomszédsági mátrix) nevezzük. A gráf mátrixa a főátlóra nézve szimmetrikus.
Példának okáért tekintsük az alábbi gráfot és annak adjacencia-mátrixát:

Az általános pakolási feladatra igazán jó algoritmus nem ismeretes. Próbálgatós módszerekkel végig lehet vizsgálni az összes független halmazokat. A második példában a feladat a gráfok nyelvén annak megállapítása, hogy összefüggő-e a fővárosokat jelképező gráf vagy sem.
Itt egy egyszerű eljárásra ad lehetőséget az alábbi észrevétel: tekintsük a gráf egy élét. Legyenek ennek végpontjai A és B. Ezt az élt röviden (AB) élnek hívhatjuk. Jelöljük G’-vel az (AB) él összehúzásával kapott gráfot. Ebben A-t és B-t egy új ponttal helyettesítjük és ezt az új pontot mindazon régi pontokkal összekötjük, amelyekkel akár az A, akár a B össze volt kötve (lásd ábra).
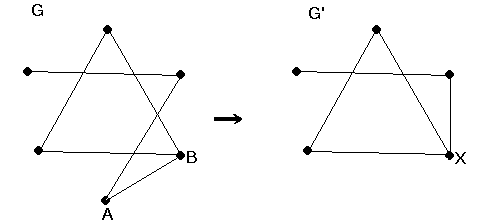
Látható, hogy G’ akkor és csak akkor összefüggő, ha G is az.
Lefordítva ezt az adjacencia-mátrix nyelvére, az alábbi eljárást kapjuk: jelölje n a pontok számát. Tegyük fel, hogy az első sorban van egy pozitív elem, legyen ez például az i-edik helyen. Adjuk hozzá az első sort az i-edikhez, majd az első oszlopot az i-edikhez, az alábbi értelemben:
0+0=0, 0+1=1+0=1+1=1
Hagyjuk el az első sort és első oszlopot és az i-edik sor i-edik helyén létrejött 1-est változtassuk 0-ra. Ismételjük meg az eljárást. Ha közben eljutunk egy 1*1-es mátrixhoz, akkor a gráf összefüggő. Ha valahol elakadunk, mert az első sorban csupa nullák állnak, akkor a gráf nem összefüggő.
A legrövidebb út kérdése
Fontos kérdés lehet az összefüggőség mellett a legrövidebb összeköttetésé. Gráfokra ez így hangzik: adott egy gráf és benne két pont, A és B. Keressük meg az A-ból B-be vezető legrövidebb utat!
Általánosabban megfogalmazva: minden X ponthoz keressünk egy A-ból X-be vezető legrövidebb utat! Ezt úgy tesszük meg, hogy az i=1, 2, ... értékekre rendre megkeressük azokat a pontokat, melyek i hosszúságú úton elérhetők (feltételezzük, hogy bármely két szomszédos pont távolsága 1 egység). Az A-ből 1 hosszúságú úton elérhető pontokat jelöljük meg az 1-es számmal és színezzük az A-ből hozzájuk vezető éleket pl. pirosra. Keressük meg most mindazokat a pontokat, amelyeknek még nincs számuk és amelyek 1-es pontból élen elérhetők. Minden ilyen pontot jelöljünk meg 2-essel és színezzünk pirosra egy-egy beléjük befutó élt. Egy A-ból kettő hosszúságú úton elérhető pont az 1-es jelű pontok valamelyikén át érhető el, így 2-essel pontosan azok a pontok vannak megjelölve, amelyek A-ból elérhetők 2, de nem 1 hosszúságú úton. Folytatva az eljárást ha már az 1, 2, ..., i számokkal megcímkéztük a megfelelő pontokat, akkor jelöljük (i+1)-gyel azokat a pontokat, amelyeknek még nincs számuk és amelyek elérhetők egy i-vel jelzett pontból élen, majd fessünk pirosra minden ilyen ponthoz egy-egy olyan élt, mely i-vel jelzett pontból fut bele.
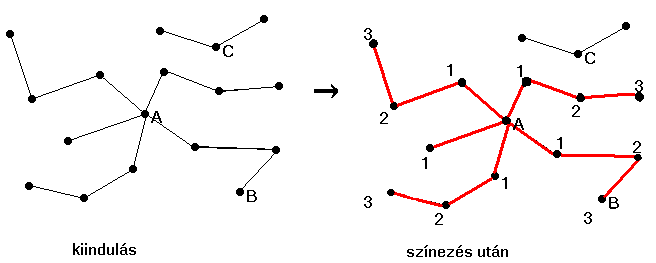
Az ábrán látható kiindulási gráf esetén az A pontból a B pont elérhető, 3 egységnyi hosszúságú úton, míg a C pont A-ból nem érhető el.
Az eljárás akkor ér véget, ha nincsen (i+1)-gyel megjelölendő
pont. Vegyük most a B pontot. Ha ez nem kapott számot, akkor nem érhető
el A-ból úton. Ha kapott számot, akkor ez az i szám lesz az A-ból B-be
vezető legrövidebb út. Egy ilyen utat kapunk, ha a piros éleken át B-ből
rendre
i-1, i-2, ...,2, 1 jelzésű
pontokon visszamegyünk A-ba.
vissza a főmenühöz!