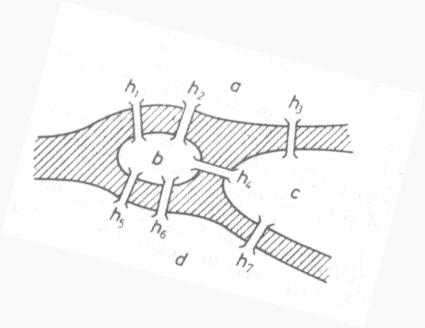
1. A Königsbergi hidak problémája: Königsberg városát átszelő Pregel folyót hét híd ívelte át az 1. ábrán látható módon. A város polgárai felvetették a kérdést, hogy lehet-e olyan sétát tenni, hogy közben mind a hét hídon pontosan egyszer haladjanak át.
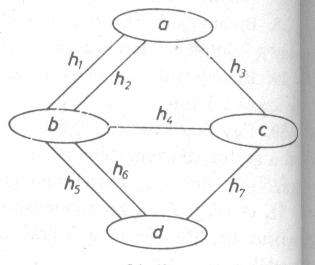
A probléma megoldásáért felkeresték Eulert, a kor híres matematikusát. Euler megoldotta a problémát és bebizonyította, hogy mind hét hídon pontosan egyszer áthaladó sétaút nem létezik. Fogalmazzuk át a feladatot a gráfok nyelvére. A két partot valamint a két szigetet jelöljük egy-egy betűvel (“a” és “d” a partokat, “b” és “c” a szigeteket jelöljék). A hidakat jelöljük “h” betűvel (h1-től h7-ig). Így juthatunk a 2. ábrához.


|
|
Látható, hogy mind a négy pont fokszáma páratlan. Ha mondjuk az “a” pontról indulunk, akkor itt nem végezhetjük a sétát, mert annak, hogy az “a” pontban fejezzük be a sétát, az a feltétele, hogy az “a” pont fokszáma páros legyen. Mind a négy pont fokszáma páratlan, de ezek közül csak egy lehet kiinduló pont és egy másik a séta utolsó állomása. Ugyanakkor a maradék két pontból is ki kellene tudni jönni, ami nem lehetséges, mert be-ki-be miatt ott kell maradnunk az adott pontban. De 3 végpontja nem lehet egyszerre ugyanannak a sétának. Ez viszont azt jelenti, hogy a feltételeknek megfelelő séta nem létezik. A megoldásból az is következik, hogy a feladatnak megfelelő séta csak akkor létezik, ha a pontok közül 2 vagy 0 darab olyan pont van, amelyeknek a fokszáma páratlan. Ha két darab páratlan fokú pont van a gráf pontjai között (a többi pedig páros fokszámú pont), akkor valamelyik páratlan fokú pontból kell, hogy induljon a sétánk és a másik páratlan fokú pontban kell, hogy végződjön.
2. Bizonyítsuk be, hogy ha 2n számú telefonközpont mindegyikének van a többiek közül legalább n-nel közvetlen összeköttetése, akkor bármely két központ között létesíthető telefonkapcsolat (esetleg közvetett módon).
A feladatot a gráfok nyelvére átfogalmazva: azt kell belátni,
hogy ha egy legfeljebb 2n-pontú egyszerű gráf minden pontjának foka legalább
n, akkor a gráf összefüggő! A bizonyítást végezzük el indirekt módon. Tegyük
fel, hogy a gráf nem összefüggő. Ekkor a gráf 1-nél több komponensből áll.
A komponensek között kell legyen olyan, amelyben nem lehet n-nél
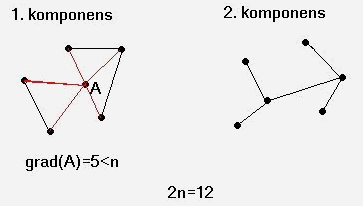
több pont. Egy ilyen komponensbe tartozó bármely A
pont csak ugyanezen komponensbe tartozó pontokkal lehet összekötve. Mivel
a gráf egyszerű, ezért grad(A)<=n-1. Ez viszont
ellentmond annak a feltételnek, hogy az eredeti gráfban minden pont fokszáma
legalább n!
3. Bizonyítsuk be, hogy ha n számú telefonközpont közül bármely kettő között létesíthető kapcsolat, akkor van e központok között n-1 számú közvetlen összeköttetés is.
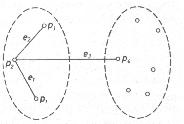
Azt kell belátni, hogy az n pontú összefüggő és egyszerű gráfnak legalább n-1 éle van. A bizonyításban azt használjuk ki, hogy bárhogyan is osztjuk fel egy összefüggő gráf pontjait két csoportba, mindig van a gráfnak olyan éle, amelynek két végpontja különböző csoportokba tartozik (lásd ábra).
Vegyük az n-pontú összefüggő egyszerű gráf egy tetszőleges p1 pontját. Ha van G-nek p1–től különböző pontja, akkor a fent említett két csoport egyike álljon csupán p1–ből. Van tehát G-nek p1–hez illeszkedő e1 éle. Jelöljük e1–nek p1–től különböző végpontját p2–vel. Ha van G-nek p1–től és p2–től különböző pontja, akkor a fent említett két csoport egyike álljon most p1–ből és p2–ből. Van tehát G-nek olyan e2 éle, amelynek egyik végpontja p1 vagy p2, a másik pedig p1–től is és p2–től is különböző. Jelöljük ezt p3–mal. Nyilván e1? e2 . Az ábrán a szaggatott vonalak a pontok újabb két csoportba osztását jelzik. Folytatva az eljárást végül találunk G-ben n-1 számú élt. Ezzel beláttuk az állítást.
4. Az n-pontú és n-1 élű összefüggő gráfok fák.
Ha volna egy n-pontú és n-1 élű, kört tartalmazó összefüggő gráf, akkor annak egy körbe tartozó élét törölve, n-pontú és n-2 élű összefüggő gráfot kapnánk. Ez viszont ellentétben áll azzal az állítással, mely szerint egy n-pontú összefüggő gráfnak legalább n-1 éle van.
Ez az állítás a minimális
számú élt tartalmazó összefüggő gráfok egy jellemző tulajdonságát adja.
5. A paraffinmolekulák n számú szénatomból és 2n+2 számú hidrogénatomból állnak. Általános képletük:
CnH2n+2 (n=1,2,3,...)
Molekuláris modelljeik összefüggő gráfokkal szemléltethetők. Ezekben a gráfokban a szénatomokat azonosító pontok fokszáma 4, a hidrogénatomokat jelképező pontok fokszáma pedig 1. Szemléltessük gráfokkal a paraffinok molekuláris modelljeit az n=1,2,3 és 4 esetben.
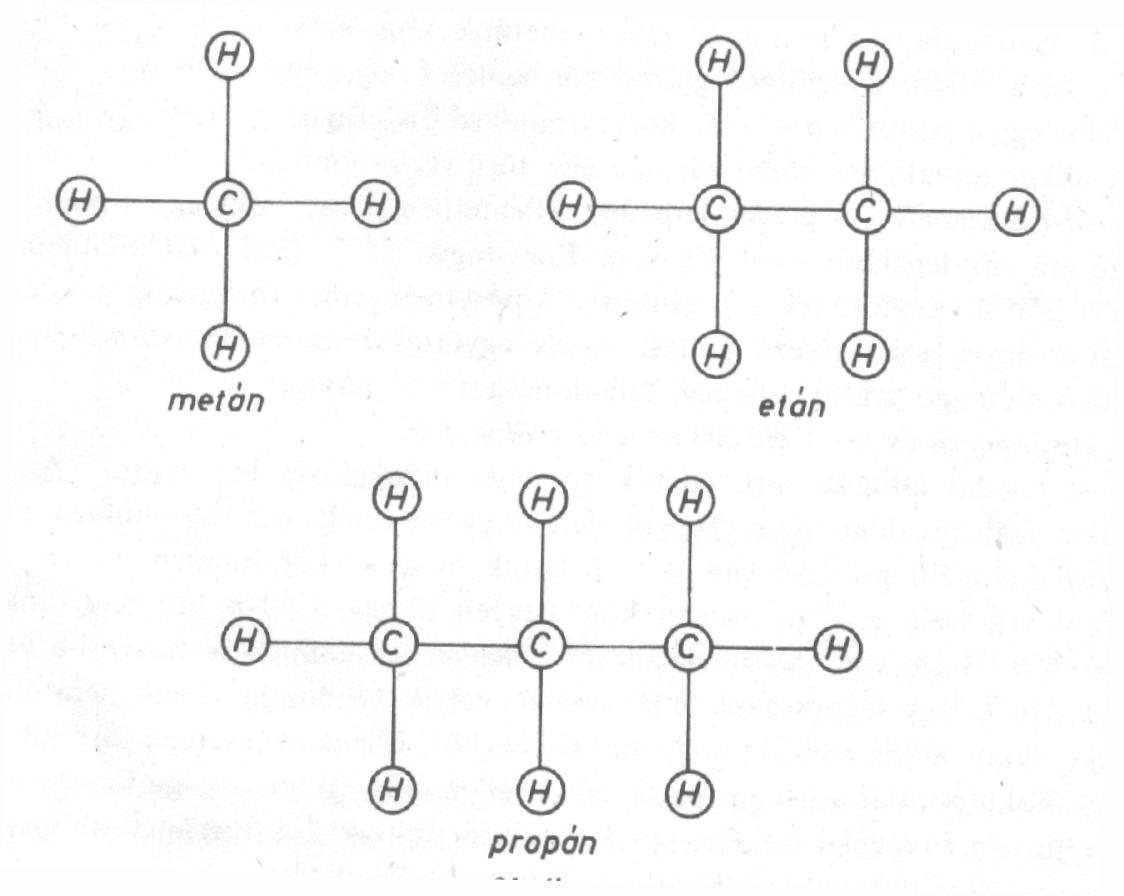
n=1, 2 és 3 esetén
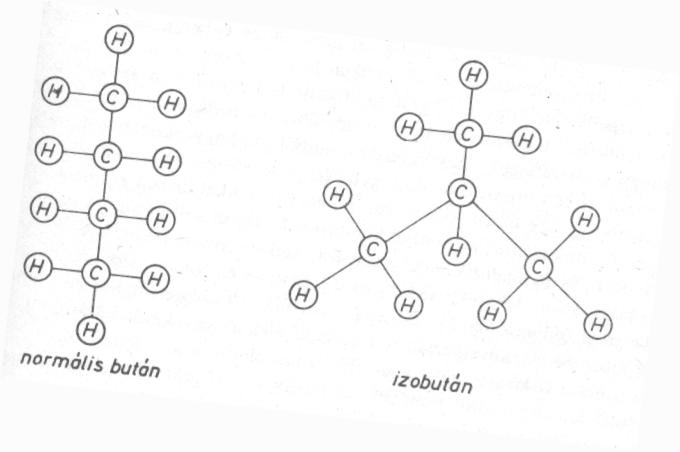
n=4 esetén
6. Bizonyítsuk be, hogy egy hattagú társaságnak mindig van vagy három olyan tagja, akik ismerik egymást, vagy három olyan tagja, akik nem ismerik egymást!
A feladatot a gráfok nyelvére a következő módon lehet átfogalmazni: minden 6-pontú egyszerű gráfnak vagy a komplementerének van háromszög részgráfja. Vegyük a 6-pontú egyszerű gráf egy tetszőleges A pontját. Osszuk a maradék 5 pontot két csoportba úgy, hogy az egyikbe azok kerüljenek, amelyek össze vannak kötve A-val, a másik csoportba pedig azok, amelyek nincsenek összekötve A-val. Az egyik csoportba mindenképpen legalább 3 pont kerül. Legyen ez a 3 pont B, C és D. Ha ezek a pontok össze vannak kötve A-val, továbbá valamelyik kettő egymással is, akkor van egy olyan hármas, amelyben bármely két pont éllel össze van kötve (az adott 3 ember tehát ismeri egymást). Ha a 3 pont mindegyike össze van kötve A-val, de egymással nincsenek összekötve, akkor van 3 olyan pont (B, C és D), amelyek között nincs él, tehát ezek az emberek nem ismerik egymást. Ha az A pont nincs összekötve a B, C és D pontok egyikével sem, és ezen utóbbi pontok között van 2 olyan, amelyek szintén nincsenek összekötve, akkor ez a két pont, valamint az A pont egy olyan hármast alkotnak, amelyhez tartozó emberek nem ismerik egymást. Ugyanakkor, ha a B, C és D pontok között nincsen 2 olyan, amelyek nincsenek éllel összekötve (vagyis bármelyik kettő között halad él), akkor ezek az emberek hárman ismerik egymást. Ezzel beláttuk az állítást!
vissza a főmenübe!