1. feladat: Egy n*n-es táblázat minden mezőjében egy betű áll. A táblázat bármely két sora különböző. Bizonyítsuk be, hogy a táblázatnak van olyan oszlopa, amelyiket elhagyva a megmaradó táblázatnak nincs két egyező sora! (Kürschák József Matematikai Tanulóverseny-1979. év 3. feladata)

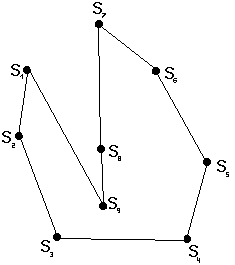
Bizonyítás: Tegyük fel indirekt, hogy az állítás nem igaz. Ekkor minden oszlophoz tartozna legalább két olyan sor, amelyik csak az adott oszlopbeli betűben különbözik. Minden oszlophoz válasszunk ki egy ilyen sorpárt. Ezt a kiválasztást szemléltethetjük úgy, hogy az i-dik sort egy S_i ponttal ábrázoljuk és ha az i-dik és j-edik sor egy kiválasztott sorpár, akkor az S_i és S_j pontokat összekötjük egy vonallal. Így egy gráfot kapunk.

A gráfnak n pontja van (az ábrán n=9) és ugyanannyi éle. Az Alapfogalmak 5. tétele szerint az ilyen gráfban mindig van kör. Az adott kör a táblázatra nézve azt jelenti, hogy az i₁ -ik és i₂ -ik sor csak egy betűben, mondjuk a j-edik oszlopbeliben különbözik. Az előbbiben itt legyen a₁, az utóbbiban pedig egy ettől különböző a₂ betű áll. Az i₂ -ik és i₃ -ik sor is csak egy betűben különbözik és ezek egy másik oszlopban állnak, tehát az i₃ -ik sor j-edik betűje szintén a₂. Hasonlóan az i₄ -ik, … i_k -ik j-edik betűje is a₂ . De az i_k -ik és i₁ -ik sor is csupán egy betűben különbözik és ezek is egy, a j-ediktől különböző oszlopban állnak. Így az i₁ -ik sor j-edik betűje is a₂ kellene, hogy legyen. Ott viszont az a₂ -től különböző a₁ betű áll. Így abból a feltevésből kiindulva, hogy bármelyik sor elhagyásával keletkezik két egyező sor, ellentmondásra jutottunk. Tehát igaz az eredeti állítás.

2. feladat: Egy tíztagú társaság minden tagja legalább hét másikat ismer. Mutassuk meg, hogy bármely három embernek van közös ismerőse! (OKTV 1986. év, II. forduló, 3. feladata, I. kategória)

Bizonyítás: Feleltessünk meg az embereknek pontokat és ha két ember ismeri egymást, akkor kössük össze őket egy vonallal. Így egy gráfot kapunk. Átfogalmazva a feladatot gráfokra, az a következőképpen szólna: ha 10 pont mindegyikét legalább 7 másikkal vonal köti össze, akkor a pontok közül bármelyik háromhoz vezet három, közös végpontú vonal. Vagy más megfogalmazásban: ha egy 10 pontú egyszerű gráf minden pontjának fokszáma legalább 7, akkor bármely 3 pontjának van közös szomszédja.

A 10 pontból tetszőlegesen válasszunk ki kettőt. Legyenek ezek A és B. Ennek a két pontnak legalább 4 közös szomszédja van a gráfban. Ha ugyanis legfeljebb 3 közös szomszédjuk volna, akkor A és B ezeken és egymáson kívül legalább még 3-3, azaz összesen legalább 6 egymástól különböző ponttal össze volna kötve. Ekkor viszont legalább 11 pontból állna a gráf (A és B az két pont, a három közös szomszéd és még hat pont, az összesen 11 pont), holott csupán 10 pontja van a gráfnak.

Tekintsük a gráf egy további C pontját. Ha ez a pont az A és B pontok közös szomszédain kívüli pont, akkor a közös szomszédokon kívül legfeljebb 5 másik ponttal lehet összekötve. De a feladat feltételei szerint még legalább 2 másik ponttal is össze kell legyen kötve. Kell tehát, hogy ebből a C pontból vezessen él az A és B közös szomszédai egyikéhez is. Így A és B valamint C mindegyike össze van kötve ezzel a közös szomszéddal, ami visszafordítva azt jelenti, hogy A, B és C-nek ez a személy közös ismerőse. Ha ez a C pont az A és B közös szomszédai közül az egyik pont, akkor a közös szomszédokon kívül legfeljebb 6 másik ponttal lehet összekötve. Így még valamelyik közös szomszéddal is össze kell legyen kötve ez a pont, nevezzük ezt a pontot D-nek. Megint azt kaptuk, hogy az A, B és C pontok mindegyike össze van kötve D-vel, vagyis visszafordítva: A, B és C ismerik D-t. Ezzel bebizonyítottuk az állítást.

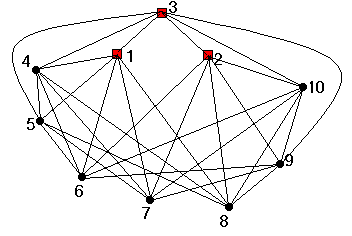
Megmutatható, hogy a feladat szövegében szereplő 10 és 7 számok éles korlátot jelentenek, egyik sem növelhető illetve a másik sem csökkenthető a feladat általánosításának csorbítása nélkül. Erre látható egy példa az alábbi ábrán. Itt a 10 pontú gráf minden pontjának fokszáma éppen 6, de van három olyan pont (1, 2 és 3), amelyeknek nincs közös szomszédja. Lásd az ábrát alant.

3. feladat: Legyen a G összefüggő gráf éleinek száma k. Bizonyítsuk be, hogy meg lehet az éleket számozni az 1, 2, 3, …, k számokkal úgy, hogy minden olyan csúcs esetén, amelyből legalább két él indul ki, az illető csúcsokból kiinduló összes élhez rendelt számok legnagyobb közös osztója 1 legyen! (NMD feladat 1991/4)

Bizonyítás: Tudjuk, hogy egy gráfban a páratlan fokú pontok száma páros (Alapfogalmak-2. tétel). Foglaljuk párokba a páratlan csúcsokat és kössük össze ezeket piros színű éllel ( a gráf eredeti élei feketék). Az így adódó gráf (amely az eredeti gráf részgráfja) minden csúcsa most már páros fokú. Az eredeti gráffal együtt tekintve, előfordulhat, hogy két csúcsot egy fekete és egy piros él is összeköt, de egy csúcsból így természetesen legfeljebb egy piros él indulhat ki. Az eredeti gráfunk ezen új élek berajzolásával ún. Euler-féle gráf lett. Ennek jellemző tulajdonsága, hogy egy tetszőleges gráfcsúcsból kiindulva a gráf élei bejárhatók úgy, hogy minden élen egyszer és csak egyszer haladjunk át és visszaérkezzünk a kiindulási pontba.

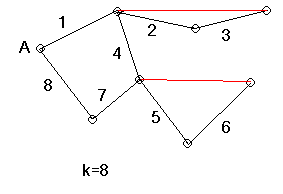
Járjuk be a kiegészített gráf éleit a következő eljárás szerint: az A csúcsból kiindulva a kiindulási fekete élre 1-est írunk és a haladásnak megfelelően minden új fekete élre 1-gyel nagyobb számot írunk rá. Ha közben piros élen haladunk át, arra nem írunk számot. Mivel az Euler-féle vonal (kör) minden élt tartalmaz, ezért az eredeti gráf minden élére fog kerülni szám. Ha egy csúcsban csak fekete él van, biztosan van rajtuk két szomszédos szám. Ezek viszont relatív prímek. Ha egy csúcsnál a piros él mellett még legalább három fekete él van (pontosan kettő nem lehet, mert akkor nem lenne ott piros vonal!), akkor az adott csúcson az Euler-vonal legalább kétszer áthalad, és így az egyik áthaladásnál fekete élhez fekete él fog csatlakozni, tehát itt is van valamelyik élpáron szomszédos szám. Ha egy csúcs piros élt is tartalmaz és mellette egy fekete él van, akkor teljesen mindegy a feladat szempontjából, hogy a fekete élen milyen szám áll. Ezzel az eljárással a feladat követelményeit teljesítettük.