1. Körmentes vízhálózat gazdaságos építése:

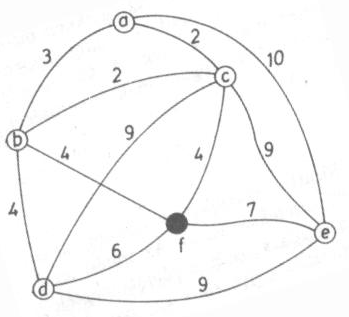
Tegyük fel, hogy falvaknak egy rendszerét vízvezeték-hálózatba akarjuk bekapcsolni. Az építési tervet úgy kell elkészíteni, hogy megvalósítása gazdaságos és a célnak megfelelő legyen. Egy térképvázlatot készítünk. A falvaknak pontokat feleltetünk meg. Ha két falu között van vezeték, akkor az azokat jelképező pontokat összekötjük egy éllel. Így kapjuk a feladatnak megfelelő gráfot. A víznek minden faluba el kell jutnia, tehát a gráfnak összefüggőnek kell lennie. A gazdaságosság megköveteli, hogy feleslegesen ne építsünk vezetéket két falu között. Ez megköveteli, hogy a gráfunk ne tartalmazzon kört! A tervrajznak megfelelő gráf tehát fagráf kell legyen, mégpedig azok közül is a legolcsóbb. A gráfok nyelvén megfogalmazva a feladatot: vegyünk fel egy olyan gráfot, melynek pontjai a falvakat, élei a falupárok között szóba jöhető vezetékeket jelölik. Számítsuk ki a falupárokat összekötő vezetékek építési költségeit és írjuk rá a megfelelő élekre. Két falunak megfelelő pontot csak egy éllel kötünk össze, mégpedig a legolcsóbb vezetéknek megfelelően. Igy az eredeti gráf egy részgráfját kapjuk, mégpedig a G gráf egy minimális építési költségű F favázát (gazdaságos favázát). Az 1. ábrán látható gráf egy építést megelőző térképvázlat. A fekete "f" pont a forrást jelöli. Ebből az "a", "b", "c", "d" és "e" pontokkal jelölt falvakat kell vízzel ellátni. Vezetékek a gráf élei mentén építhetők. Az élekre rá vannak írva a vezetékek építési költségei.

1. módszer: Az összefüggő G gráf egy gazdaságos favázát keressük. Töröljünk G-nek körökben szereplő élei közül egy legnagyobb költségűt. Az így kapott G_{1 grág G-nek egy részgráfja és G1} összefüggő és G-nek minden pontját tartalmazza. Ezután töröljük G₁ köreiben szereplő élek közül egy legnagyobb költségűt, majd ismételjük tovább ezt az eljárást. Ha a törlési utasítás már nem hajtható végre, akkor az utolsónak kapott F gráfnak már nincs köre és F a G gráfnak részgráfja továbbá összefüggő is, azaz F egy fagráf.

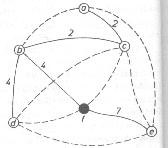
Az 1. ábrán látható gráf esetén először vegyük az a-c-e-a kört. Ebben a legnagyobb élű a 10-es, ezt töröljük (az ábrán szaggatott vonallal jelöljük a továbbiakban). A f-e-c-f körben a 9-es élt kell törölnünk az eljárás szerint. A d-f-c-d körben szintén a 9-es élt kell törölnünk. A d-f-e-d körben a 9-es élt kell törölnünk. A d-f-b-d körben a d-f közötti 6 hosszúságú élt, az f-c-b-f körben az f-c közötti 4 hosszúságú élt, valamint a b-c-a-b körben a b-a közötti 3 hosszúságú élt kell törölni. Ezeket az éleket mind törölve kapjuk a 2. ábrát, amelyen a folytonos vonallal jelölt (és számmal ellátott!) F gráf lesz a G gráf egy gazdaságos faváza. Ebben az élekre írt szakaszok költségeinek összege: 19 egység.

Bebizonyítható, hogy ez az F fagráf a G gráfnak gazdaságos fagráfja.

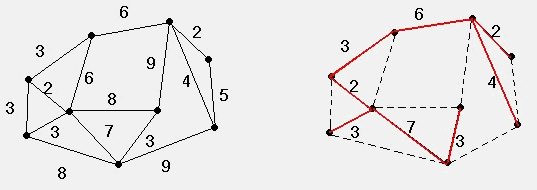
 2. módszer: Jelöljük ki az összefüggő gráf egy legkisebb költségű élét. Minden további élt a lehető legkisebb költségűek közül jelöljünk ki, ügyelve arra, hogy G egyetlen körének se legyen valamennyi éle kijelölt. Az előbbihez hasonló módon be lehet látni, hogy ha az utasításnak megfelelően már nem jelölhető ki él, akkor G egy gazdaságos favázának éleit jelöltük ki. Alkalmazva ezt a módszert az alábbi, bal oldali ábrán levő gráfra, az eljárás végén a jobboldali gráfot kapjuk. Ennek építési költsége 30 egység.