Most bizonyítsuk be, hogy jól okoskodtunk!
1 + 2 + ... + (n-1) + n + (n-1) + ... + 2 + 1 = *
Csoportosítsuk a tagokat a következőképpen:
* = (1 + n-1) + (2 + n-2) + ... + (n-2 + 2) + (n-1 + 1) + n
= n * n
= n2

| s(n) = 1 + 2 + 3 + 4 + ... + n = | n(n+1) |
|
2
|
| s(1) = | 1*2 |
|
2
|
| s(2) = 1 + 2 = 3 = | 2*3 |
|
2
|
| s(3) = 1 + 2 + 3 = 6 = | 3*4 |
|
2
|
| s(4) = 1 + 2 + 3 + 4 = 10 = | 4*5 |
|
2
|
| s(n) = 1 + 2 + 3 + 4 + ... + n = | n(n+1) |
|
2
|
| s(k) = | k(k+1) |
|
2
|
| s(k+1) = 1 + 2 + 3 + ... + k + k+1 = | (k+1)(k+2) |
|
2
|
| k(k+1) |
= k + 1 =
|
(k+1)(k+2)
|
|
2
|
2
|
| s(n) = a1 + a2 + a3 + ... + a n = n | a1+an |
|
2
|
| s(n) = 1 + 2 + 3 + ... + n = n | 1+n |
=
|
n(n+1)
|
|
2
|
2
|
 c/1
c/1 |
n2
|
+
|
n
|
|
|
|
|
|
2
|
2
|
|
s(n) = 1 + 2 + 3 +... + n =
|
n2
|
+
|
n
|
=
|
n(n+1)
|
|
|
|
|
|||
|
2
|
2
|
2
|
|
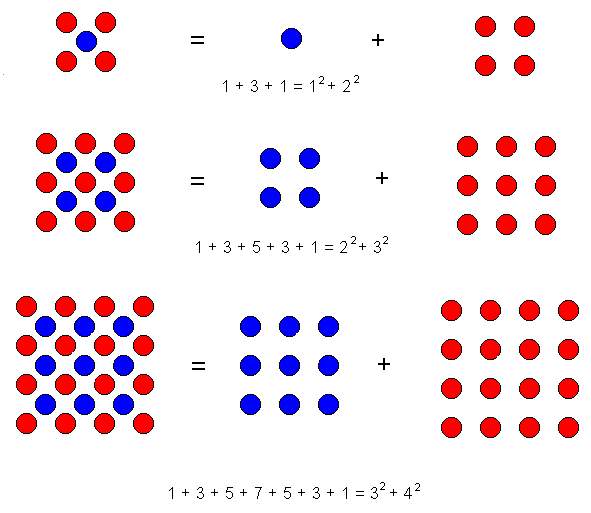
s(n2) = 1
2 + 22
+ ... + n2=
|
n(n+1)(2n+1)
|
|
|
|
|
6
|
|
|
n = 1
|
n = 2
|
|
n = 3
|
|
n = 4
|
|
n = 5
|
...
|
n
|
|
s(n)
|
1
|
3
|
6
|
10
|
15
|
...
|
n(n+1) |
|||
|
|
||||||||||
|
2
|
||||||||||
|
s(n2)
|
1
|
5
|
14
|
30
|
55
|
...
|
?
|
|||
|
s(n2)
|
1
|
5
|
14
|
30
|
55
|
...
|
2n+1
|
|||
|
|
|
|
|
|
|
|||||
|
s(n)
|
3
|
6
|
10
|
15
|
3
|
| s(n2) = s(n) |
2n+1
|
= |
n(n+1)(2n+1) |
|
|
|
||
|
3
|
6
|
| s(k2) = |
k(k+1)(2k+1)
|
|
6
|
| s((k+1)2) = 12 + 2 2 + 32 + ... + k2 + (k+1)2 = |
(k+1)(k+2)(2k+3)
|
|
6
|
| k(k+1)(2k+1) |
+ (k+1)2 =
|
(k+1)(k+2)(2k+3)
|
|
|
|
|
|
6
|
6
|
| 1 + 2 + 3 + ... + n = | n(n+1) |
|
2
|
| 13 + 23 + 33 + ... + (n-1) 3 = ( 13 + 2 3 + 33 + ... + n 3) - 3(1 2 + 22 + 32 + ... + n 2 ) + 3 | n(n+1) |
- n |
| 2 |
|
1 + 22 + 32 + ... + n
2 =
|
n(n+1)
|
+
|
n3-n
|
=
|
3n(n+1) + 2(n3-n)
|
=
|
3n(n+1) + 2n(n2-1)
|
|
|
|
|
|
||||
|
2
|
3
|
6
|
6
|
|
=
|
3n(n+1)+2n(n+1)(n-1)
|
=
|
n(n+1)(3+2n(n-1)
|
=
|
n(n+1)(2n+n)
|
|
|
|
|
|||
|
6
|
6
|
6
|
| sn = 1 + 3 + 5 + ... + (2n-1) = n | 1 + (2n-1) |
=
|
2n2
|
= n2 |
|
|
|
|||
|
2
|
2
|

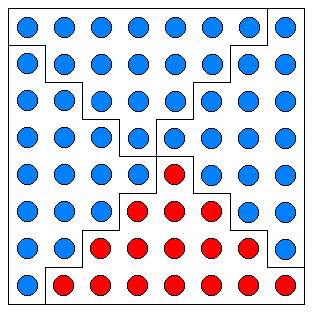
| 1 + 3 + 5 + ... + (2n-1) = | 1 |
*(2n)2 = n2
|
|
|
||
| 4 |
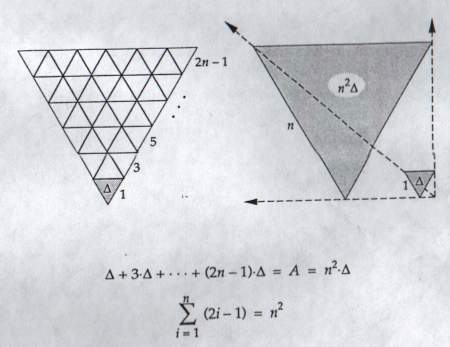
|
n
|
2i-1 = n2
|
|
|
|
|
i=1
|
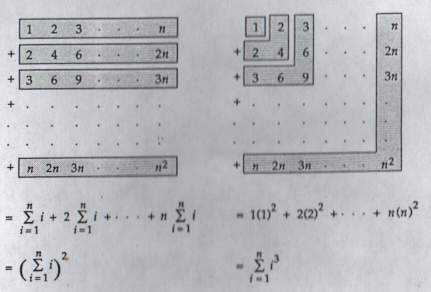
| s(n3) = 13 + 23 +
... + n3 = |
(n(n+1))2 |
|
(2)2
|
| 13 + 23 + ... + n3
= (1 + 2 + 3 + ... + n)2 = |
(n(n+1))2 |
|
(2)2
|
| s(k3) = 13 + 23 + ...
+ k 3 = |
(k(k+1))2 |
|
(2)2
|
| s((k+1)3) = 13 + 23
+ ... + k3 + (k+1)3 = |
((k+1)(k+2))2 |
|
( 2)2
|
| (k(k+1))2 |
+ (k+1)3 =
|
((k+1)(k+2))2
|
|
(2)2
|
(2)2
|
|
12 + 22 + ... + n2
=
|
(n(n+1)(2n+1))2
|
|
|
|
|
6
|
|
1 + 2 + ... + n =
|
(n(n+1))
|
|
|
|
|
2
|
|
4(13 + 23 + 33
+ ... + n3) = n4 + 6
|
n(n+1)(2n+1)
|
- 4
|
n(n+1)
|
+ n
|
|
6
|
2
|
|
13 + 23 + 33 +
... + n3 =
|
n4
|
+
|
n(n+1)(2n+1)
|
-
|
n(n+1)
|
+
|
n
|
|
|
4
|
2
|
4
|
| 13+23+.......+n3= |
(n(n+1))2 |
|
( 2)2
|
| 13 + 23 + ... + n3
= (1 + 2 + 3 + ... + n)2 = |
(n(n+1))2 |
|
(2)2
|