A sík lefedése
A háromszögek egybevágósági alapesetei,
melyek az abszolút geometria eszközeivel bizonyított tételek, egy újabb
tétellel bővülnek a hiperbolikus geometriában. Kihasználva, hogy
bármely háromszög defektusa pozitív, könnyen igazolható, hogy:
Két háromszög egybevágó, ha
szögei páronként egyenlők.
|
Itt most a szögeivel adunk meg olyan háromszögeket, amelyekkel hézagmentesen
kiparkettázható a hiperbolikus sík úgy, hogy a szomszédos háromszögek a
közös oldalegyenesükre vonatkozóan egymás tengelyes tükörképei legyenek.
Ennek az a feltétele, hogy a háromszög mindhárom szöge a teljes szög
k- ad része (vagy 0° ) legyen, ahol k egész
szám, emellett teljesüljön, hogy a háromszög defektusa pozitív. Ha valamely
szögre nézve k páratlan, akkor a parkettázás
csak akkor végezhető el, ha a háromszög egyenlőszárú, azaz a másik két
szöge egyenlő. Ebben az esetben azonban nem tudjuk kiszínezni a háromszögeket
két színnel úgy, hogy a szomszédos háromszögek különböző színűek legyenek,
ezért ilyenkor véletlenszerűen választott
színekkel végezzük a színezést. Ha mindhárom szög a teljes szög 2k
-ad része, (vagy 0° ), akkor két színnel végezzük
a lefedett síkrész színezését.
Itt jegyezzük meg, hogy:
Az euklídeszi síkban mindössze
négy olyan háromszög létezik, amellyel a feltételeknek eleget tevő parkettázás
megvalósítható. Ezek szögei rendre ( 90°
, 60° , 30°
) ; (90° , 45° ,
45° ) ; (60° , 60°
, 60° ) ; (120° ,
30° , 30° ). A két
utóbbi a derékszögűekből is előállítható.
|
A hiperbolikus síkot végtelen sokféle háromszöggel ki lehet
parkettázni a feltételnek eleget tevő módon.
|
Az euklídeszi sík a szabályos sokszögek közül csak a szabályos háromszöggel,
a négyzettel és a szabályos hatszöggel parkettázható ki.
|
A hiperbolikus sík kiparkettázható
minden olyan szabályos n - szöggel, amelynek minden szöge a teljes szög
k -ad része , ahol k >2 tetszőleges, ekkor 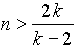 egész szám, vagy minden szöge 0° , (ekkor n>2
).
egész szám, vagy minden szöge 0° , (ekkor n>2
).
|
Már említettük, hogy a hiperbolikus geometriában
van legnagyobb területű háromszög, melynek mindhárom szöge 0°
-os. Azonban ebből is végtelen sokkal
lehet csak lefedni a síkot, tehát maga a sík területe nem véges.
A programrészletet vizsgálva támadhat
olyan érzésünk, mintha a modell középpontjának kitüntetett szerepe lenne
a parkettázásban. Ez nem így van, véletlenszerűen is elhelyezhetjük a kiindulásul
vett háromszöget.
<<<<<