Egy érdekes geometriai alakzat: az Oloid
Készítette: dr Szilassi Lajos
HANS DIRBÖCK és HELMUTH STACHEL: The Development of the Oloid (Journal for Geometry and Graphics Volume 1 (1977) No2. 105-118) c. cikk felhasználásával.
E-mail: szilassi@jgytf.u-szeged.hu

> restart: with(plots):with(plottools):

Warning, the name changecoords has been redefined

A feladat

Adott a síkban két ugyanakkora - egységnyi - sugarú kör, melyek síkjai merőlegesek egymásra, és középpontjaik távolsága egységnyi. Így mindkét körvonal illeszkedik a másik kör középpontjára. Oloid nak nevezzük a két kör konvex burkát: azt a legkisebb konvex térgeometriai alakzatot, amely mindkét kört tartalmazza.

Feladatunk az, hogy ennek az alakzatnak a tulajdonságait megismerjük.

Az oloidot meghatározó köröket úgy helyezzük koordinátarendszerbe, hogy az alakzat legyen szimmetrikus az origóra.
A ka kör az xy síkban, a kb az xz síkban helyezkedjék el

>

rajz1: bemutatjuk a két körlapot

n: a beosztás finomsága;
a és b a két körvonal pontjai, CA és CB a két körlap RV a körvonalak rajza.

> n:=30:
a:=[seq( [ 1/2+cos(i*2*Pi/n),sin(i*2*Pi/n),0],i=1..n)]:
b:=[seq( [-1/2+cos(i*2*Pi/n),0,sin(i*2*Pi/n)],i=1..n)]:
CA:=polygonplot3d(a, color=yellow):
CB:=polygonplot3d(b,color=cyan):
RV:=polygonplot3d([a,b],linestyle=16,style=wireframe,color=blue):

> display3d(CA,CB,RV,scaling=constrained);

Az oloid alkotói

Ha egy G geometriai alakzathoz érintősíkokat illesztünk az összes lehetséges módon, majd vesszük az ezek, mint hatásríkok által meghatározott G -t tartalmazó félterek közös részét, akkor ezzel megadtuk a G alakzat konvex burkát .

Esetünkben - mivel az alakzat az x tengely körüli derékszögű forgatásra, valamint az yz síkra szimmetrikus, elegendő azokat az érintősíkokat vizsgálni, melyek metszik az x tengely pozitív felét. (Ezekhez hozzá kell még vennünk azt az egyet, amely az x tengellyel párhuzamos.)
Legyen P:= [m,0,0] az x tengely tetszőleges pontja, M -ből az a körhöz húzott (egyik) érintő érintési pontja A:=[xb,yb,0] , a b körhöz húzott érintő B:=[xb,0,zb].

Fusson végig az A pont az a kör negyedkörén: t=[0..Pi/2)

ax, ay, bx, by a körvonalakat leíró paraméteres függvények

>

> ax:= t -> 1/2+cos(t):
ay:= sin:
bx:= t-> 1/2*(cos(t)-1)/(cos(t)+1):
bz:= t-> sqrt((2*cos(t)+1))/(cos(t)+1):

Az m paraméter értéke is kifejezhető t -vel, kihasználva, hogy OM=1/cos(t) , ahol O:=[1/2,0,0] az a kör középpontja:

> mx:= t -> 1/2+1/cos(t):

Rajz2

Ez a rajz csak akkor állítható elő, ha az R1 rajzot előzőleg előállítottuk!

> p:=1.1;

> tx:= line([mx(p)+0.5,0,0], [-2,0,0],color=blue):
ty:= line([0,-1.5,0], [0,1.5,0] ,color=blue):
tz:= line([0,0,-1.5], [0,0,1.5] ,color=blue):
MA:= line([mx(p),0,0], [ax(p),ay(p),0] ,color=red):
OA:= line([1/2,0,0], [ax(p),ay(p),0] ,color=black):

Mp:=textplot3d([mx(p),0,0,`M`],color=black):
Ap:=textplot3d([ax(p),ay(p),0,`A`],color=black):

Xp:=textplot3d([mx(p)+0.6,0,0,`X`],color=black):
Yp:=textplot3d([0,1.5,0,`Y`],color=black):
Zp:=textplot3d([0,0,1.5,`Z`],color=black):

> display3d(CA,CB,RV,
tx,ty,tz,
Mp,Ap,
MA,OA,
Xp,Yp,Zp,
scaling= constrained);

Különböző (Pi/2-nél kisebb) t értékre kipróbálhatjuk, miként változik a rajz a paraméter megválasztásától.:

Írjuk fel az M pont koordinátájában szereplő mx függvényeként az M -ből a b körhöz húzott (egyik) érintő érintési pontjának, B -nek a koordinátáit:

> bx:= t->-1/2+1/(mx(t)+1/2);
bz:= t-> sqrt(1-(bx(t)+1/2)^2);

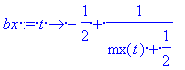
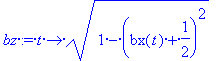
A függvényeket kiíratva (és egyszerűsítve) látható, hogy mindkét függvény egyetlen független változót tartalmaz.

> bx(t);simplify(bx(t));

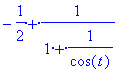
> bz(t);simplify(bz(t));

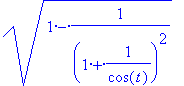
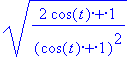
Rajz 3
Az oloid t paraméteréhez tartozó érintősíkja az ABM sík:

Ez a rajz csak akkor állítható elő, ha az R1 és R2 rajzokat is előállítottuk!

> p:=1.1:
MA:= line([mx(p),0,0], [ax(p),ay(p),0] ,color=red):
OA:= line([1/2,0,0], [ax(p),ay(p),0] ,color=black):
Xp:=textplot3d([mx(p)+0.6,0,0,`X`],color=black):
Mp:=textplot3d([mx(p),0,0,`M`],color=black):
Ap:=textplot3d([ax(p),ay(p),0,`A`],color=black):
MB:= line([mx(p), 0,0],[bx(p),0,bz(p)] ,color=red):
AB:= line([ax(p),ay(p),0],[bx(p),0,bz(p)] ,color=red):
MAB:= polygonplot3d([[mx(p), 0,0],[ax(p),ay(p),0],[bx(p),0,bz(p)]],color=cyan,style=patchnogrid):

> display3d(CA,CB,RV,
tx,ty,tz,
Mp,Ap,
MA,MB,AB,MAB,
Xp,Yp,Zp,
scaling= constrained);

I

>

Az alkotók hossza

AZ oloid MAB érintősíkja a felületet az AB szakasz mentén érinti.
Nevezzük az érintősík és az oloid közös részét az oloid alkotóinak!
Vizsgáljuk meg, miként függ a d(t)=AB alkotó hossza a t paramétertől!

> d:= t->sqrt((bx(t)-ax(t))^2+(0-ay(t))^2+(bz(t)-0)^2);

> d(t);simplify(d(t));
d(0);
limit(d(t),t=Pi/2);

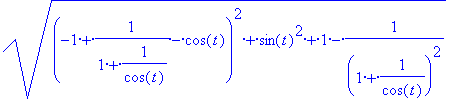
A fentiek szerint az oloid bármely alkotója ugyanakkora , a t paraméter megválasztásától függetlenül.
Ez a megállapítás t = 0 és t = Pi/2 esetre is érvényes, amikor az ABM háromszög nem létezik.

>

Az oloid megjelenítése

Az oloidról készített rajzokhoz újra definiáljuk az eddig használt változókat, így ez a programrészlet az előzőektől függetlenül is futtatható.

> restart: with(plots):with(plottools):

Warning, the name changecoords has been redefined

Ugyanazokat a változókat és függvényeket fogjuk használni:
a és b a két körvonal pontjai, CA és CB a két körlap RV a körvonalak rajza.

> n:=30:
a:=[seq( [ 1/2+cos(i*2*Pi/n),sin(i*2*Pi/n),0],i=1..n)]:
b:=[seq( [-1/2+cos(i*2*Pi/n),0,sin(i*2*Pi/n)],i=1..n)]:
CA:=polygonplot3d(a, color=yellow):
CB:=polygonplot3d(b,color=cyan):
RV:=polygonplot3d([a,b],linestyle=16,style=wireframe,color=blue):

ax, ay, bx, by a körvonalakat leíró paraméteres függvények (az egyszerűsített alakot vettük át)

> ax:= t -> 1/2+cos(t);
ay:= sin:ay(t);
bx:= t-> 1/2*(cos(t)-1)/(cos(t)+1);
bz:= t-> sqrt((2*cos(t)+1))/(cos(t)+1);

n jelentse továbbra is a beosztás finomságát. Ennek most párosnak kell lennie.
Ahhoz, hogy a t paramétert továbbra is határozatlan változóként kezelhessük, célszerű azonnal megfosztanunk a ciklusban kapott konkrét értékétől.

> n:=12:
for i from 0 to n do
t:=i*Pi/n-Pi/2:
A[i]:=[ax(t),ay(t), 0]:
B[i]:=[bx(t), 0, bz(t)]:
L[i]:=line(A[i],B[i]
, color=COLOR(HUE,(4*n+i)/8/n)
):
od:
unassign('t');

Az alkotók: (csak negyedrészüket állítottuk elő külön-külön, a többit ebből kapjuk geometriai transzformációkkal. Ugyanez vonatkozik magára a - négyszögekből álló - felületre is.)

> V1:=display3d(seq(L[i],i=0..n),insequence=false,color=orange):
V2:=rotate(V1,Pi,0,0):
V3:=rotate(V1,Pi/2,0,Pi):
V4:=rotate(V2,Pi/2,0,Pi):

> F1:=display3d(seq(polygonplot3d([A[i],A[i+1],B[i+1],B[i]]),i=0..n-1),insequence=false):
F2:=rotate(F1,Pi,0,0):
F3:=rotate(F1,Pi/2,0,Pi):
F4:=rotate(F2,Pi/2,0,Pi):
F0:=display3d(seq(polygonplot3d([A[i],A[i+1],B[i+1],B[i]]),i=0..n/2-1),insequence=false):
V0:=display3d(seq(L[i],i=0..n/2),insequence=false,color=orange):

Megjelenítések:

> display3d(CA,CB,V1,F1,scaling= constrained);

> display(F1,F2,F3,F4,scaling= constrained,
ambientlight=[0.73,0.57,0.9]
,light=[185,245,0.1,0.67,0.8]
,light=[45,45,0.7,0.74,0]
);

> display3d(RV,F0,V0,scaling= constrained);

> F0;

>

megjelenítés megadott színekkel

Minden alkotónak és minden lapnak külön-külön adunk színt, ezért nem állíthatjuk elő a felületet az első egynegyedéből, vagy egynyolcadából.
A színeket úgy választjuk, hogy az élek színe is és a lapok színe is fussa be az egész színskálát úgy, hogy az él színe mindig alap színétől "legtávolabbi" szín legyen.

> n:=6:
e:=Pi/2/n:
for i from 0 to n-1 do
t:=i*e:
A[i]:=[ax(t-Pi/2),ay(t-Pi/2), 0]:
B[i]:=[bx(t-Pi/2), 0, bz(t-Pi/2)]:

A[i+n]:=[ax(t),ay(t), 0]:
B[i+n]:=[bx(t), 0, bz(t)]:

A[i+2*n]:=[-bx(t-Pi/2),bz(t-Pi/2), 0]:
B[i+2*n]:=[-ax(t-Pi/2),0,-ay(t-Pi/2)]:

A[i+3*n]:=[-bx(t),bz(t), 0]:
B[i+3*n]:=[-ax(t),0,-ay(t)]:

A[i+4*n]:=[ax(t-Pi/2),-ay(t-Pi/2), 0]:
B[i+4*n]:=[bx(t-Pi/2), 0,-bz(t-Pi/2)]:

A[i+5*n]:=[ax(t),-ay(t), 0]:
B[i+5*n]:=[bx(t), 0,-bz(t)]:

A[i+6*n]:=[-bx(t-Pi/2),-bz(t-Pi/2), 0]:
B[i+6*n]:=[-ax(t-Pi/2),0,ay(t-Pi/2)]:

A[i+7*n]:=[-bx(t),-bz(t), 0]:
B[i+7*n]:=[-ax(t),0,ay(t)]:
od:
A[8*n]:=A[0]:
B[8*n]:=B[0]:

> for i from 0 to 8*n do
if is(i<4*n) then s:= (4*n+i)/8/n else
s:= (-4*n+i)/8/n fi:
L[i]:=line(A[i],B[i], color=COLOR(HUE,s)):
od:
unassign('t');
SV:=display3d(seq(L[i],i=0..8*n),insequence=false):
SF:=display3d(seq(polygonplot3d([A[i],A[i+1],B[i+1],B[i]],
color=COLOR(HUE,i/8/n),style=patchnogrid),i=0..8*n-1),insequence=false):

Megjelenítések

> display3d(SF,SV,scaling=constrained);

> display3d(SF,scaling=constrained);

> display3d(RV,SV,scaling=constrained);

>

Érdekes megjelenítési módhoz jutunk, ha a felületből csak minden második "sávot" rajzoljuk meg:

> SF2:=display3d(seq(polygonplot3d([A[2*i],A[2*i+1],B[2*i+1],B[2*i]],
color=COLOR(HUE,2*i/8/n),style=patchnogrid),i=0..4*n-1),insequence=false):

>

megjelenítések

> SF2;

> display3d(SF2,RV,scaling= constrained,axes=none);

> display3d(SF2,RV,SV,scaling= constrained,axes=none);

Az oloid érintősíkja

Készítsünk egy animációt, amely bemutatja, miként fut körbe az oloid felületén egy érintő-téglalap, melynek egyik középvonala az AB alkotó, az erre merőleges oldal (pl.most) 2 egységnyi.

Először előállítunk három eljárást. A "vektoriszorzat" helyett használhatnánk a linalg eljárásai közül a crossprod függvényt is, de ennek a bekapcsolása tovább terhelné - többnyire felesleges dolgokkal - a programunkat.
A - máshol is használható - egységvektort előállító eljárásnál ügyelnünk kellett arra, hogy ne álljon le a programunk 0-val való osztás miatt, ha a bemenő adata a nullvektor. (Bár ez itt nem fog előfordulni.)
Az E eljárás feladata, hogy egy AB szakaszra illessze a tervezett téglalapot.
Ennek az eljárásnak a bemenő adata az A és B pont, továbbá egy olyan V vektor, amely vagy az CA vagy a CB körlapot érinti A -ban, ill. B -ben, így biztosan benne van a keresett síkban, csak (többnyire) nem merőleges AB -re. Az eljárás lényege, hogy először előállítja erre az érintőre, valamint az AB -re merőleges N vektort, majd erre és AB -re ismét merőlegest állít,(melyet jelölhetünk ugyanazzal az N -nel) így megkapjuk az érintő téglalap AB -re merőleges oldalát.
Negyedik bemenő adat az érintősík színe, amely jelen esetben épp a felület adott érintési pontjához (pontosabban szakaszához) tartozó szín ellentétes színe, amellyel magát AB -t is rajzoltuk. Akinek szimpatikusabb lenne, ha az érintkező felületdarab és az érintősík színe legyen azonos, , írja át ezt a bemenő adatot rendre i/8/n , (i+2*n)/8/n stb.-re.

> vektoriszorzat:= (a,b) -> [a[2]*b[3]-a[3]*b[2],
a[3]*b[1]-a[1]*b[3],
a[1]*b[2]-a[2]*b[1]]:
Egysegnyi:= proc (a)
local d;
d:=sqrt(a[1]^2+a[2]^2+a[3]^2):
if is(d>0) then [a[1]/d,a[2]/d,a[3]/d]
else a; fi;
end proc:

E:=proc(A,B,V,s)
local N;
N:=vektoriszorzat(V,B-A);
N:=Egysegnyi(vektoriszorzat(N,B-A)):
polygonplot3d([A+N,A-N,B-N,B+N],color=COLOR(HUE,s));
end proc:

> e:=Pi/2/n:
for i from 0 to 2*n-1 do
t:=e*i:
ER[i ]:=E(A[i ],B[i ],[cos(t), sin(t),0],(4*n+i)/8/n):
ER[i+2*n]:=E(B[i+2*n],A[i+2*n],[cos(t),0, sin(t)],(6*n+i)/8/n):
ER[i+4*n]:=E(A[i+4*n],B[i+4*n],[cos(t),-sin(t),0],(i)/8/n):
ER[i+6*n]:=E(B[i+6*n],A[i+6*n],[cos(t),0,-sin(t)],(2*n+i)/8/n): od:
ES:=display(seq(ER[i],i=0..8*n-1),insequence=true,style=patch):

Megjelenítések

> display3d(SF,ES,scaling=constrained);

> display3d(SV,CA,CB,ES,RV,scaling=constrained);

>

Az oloid hálózata, modellkészítés

Általában vonalfelületeknek nevezzük azokat a felületeket, melyek egy egyenes, vagy egy egyenesdarab (félegyenes, ill. szakasz) -térbeli mozgásával állnak elő. Ilyen speciális vonalfelületek pl. a kúp-és hengerfelületek. Ezeknél kissé általánosabb vonalfelületek azok, amelyeket leíró egyenes úgy mozog, hogy eközben valamely térgörbét érint. Ezek a vonalfelületek síkbafejthetők, azaz kiteríthetők úgy, hogy eközben a felületen futó bármely vonal ívhossza változatlan marad.

Bizonyítható, hogy az oloid ilyen síkba kiteríthető felület. A "síkbafejtés" alaposabb differenciálgeometriai számolásokat igényel, mi itt az említett cikk eredményeit felhasználva adjuk meg a felület síkbeli hálózatát.

Ismét új önálló programrészletet készítünk.

> restart: with(plots):with(plottools):

Warning, the name changecoords has been redefined

>

A ka és kb körvonalaknak a felületre illeszkedő ívének a képét a kifejtés után egy-egy paraméteres egyenletrendszerrel írjuk le. Az alábbi függvények értelmezési tartománya a a t paraméterre nézve a [0 . . 3*Pi/2] intervallum, amelyből mi később a [0 . . Pi/2] részt fogjuk felhasználni, mivel ebből a részből az egész felület összeállítható egybevágósági transzformációkkal.

> kax:= t->2*sqrt(3)/9*(sqrt(2*(1+2*cos(t))*(1-cos(t)))+
arccos(sqrt(2)*cos(t)/sqrt(1+cos(t))));
kay:= t ->sqrt(3)/9*(4*(1-cos(t))+log(2/(1+cos(t))));
kbx:= t-> 2*sqrt(3)/9*(-sqrt(2*(1+2*cos(t))*(1-cos(t)))/(1+cos(t))+
arccos(sqrt(2)*cos(t)/sqrt(1+cos(t))));
kby:= t -> sqrt(3)/9*((11+7*cos(t))/(1+cos(t))+log(2/(1+cos(t))));

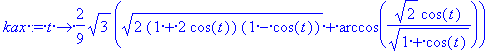
Ábrázoljuk ezeket a függvényeket, valamint az a felületre illeszkedő szakaszokat, melyek végpontjai azonos t paraméter értékhez tartoznak:

> fa:=plot([kax(t),kay(t),t=0..2*Pi/3],color=red):
fb:=plot([kbx(t),kby(t),t=0..2*Pi/3],color=blue):
n:=20: f:=2*Pi/3/n:
V:=display(seq(line([kax(i*f),kay(i*f)],[kbx(i*f),kby(i*f)]),i=0..n),
insequence=false):
display({fa,fb,V},linestyle=16,scaling= constrained);

A szakaszok egyenletesen változó t érték mellett - mint az várható volt a térbeli alakzatnál látottak alapján - 2*Pi/3 közelében "ritkábban" helyezkednek el. Ez tulajdonképpen nem baj, hiszen a [0..Pi/2] intervallumon leírt felületdarabokból összeállítható az egész alakzat, így a hálózatot is ebből fogjuk összeállítani:

> fa:=plot([kax(t),kay(t),t=0..Pi/2],color=red):
fb:=plot([kbx(t),kby(t),t=0..Pi/2],color=blue):
n:=20: f:=Pi/2/n:
V:=display(seq(line([kax(i*f),kay(i*f)],[kbx(i*f),kby(i*f)]),i=0..n),
insequence=false):
display({fa,fb,V},linestyle=16,scaling= constrained);

Egy ellenőrzési lehetőség:
Vizsgáljuk meg, hogy igaz-e, hogy az AB szakasz hossza - a t paramétertől függetlenül - a síkbafejtés után is ugyanakkora-e, mégpedig sqrt(3)!

> d:=sqrt((kbx(t)-kax(t))^2+(kby(t)-kay(t))^2);

> simplify(d);

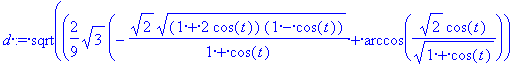
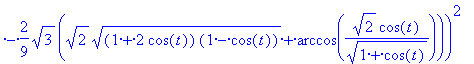
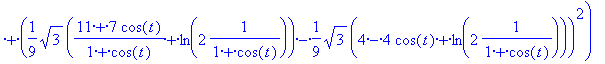
Az eredmény megnyugtató.

Az egész felület síkbafejtéséhez szükségünk lesz még a b kör képét előállító fb vonal t=2*Pi/3 értékhez tartozó pontjára, ugyanis ebbe a pontba kell eltolni, és "lefelé fordítani" az fa vonalat, hogy az pontosan leírja az fb vonal kritikus részét .

> ex:=kbx(2*Pi/3);ey:=kby(2*Pi/3);

Ennek a felhasználásával összesen nyolc egybevágó részből felépíthető a felület kifejtett képe:

> ka[0]:=plot([-kax(t),kay(t),t=0..Pi/2],color=black):
ka[1]:=plot([ kax(t),kay(t),t=0..Pi/2],color=black):
ka[2]:=plot([-kax(t)+ex,-kay(t)+ey,t=0..Pi/2],color=black):
ka[3]:=plot([ kax(t)+ex,-kay(t)+ey,t=0..Pi/2],color=black):
ka[4]:=plot([-kax(t)+2*ex,kay(t),t=0..Pi/2],color=black):
ka[5]:=plot([ kax(t)+2*ex,kay(t),t=0..Pi/2],color=black):
ka[6]:=plot([-kax(t)+3*ex,-kay(t)+ey,t=0..Pi/2],color=black):
ka[7]:=plot([ kax(t)+3*ex,-kay(t)+ey,t=0..Pi/2],color=black):

> kb[0]:=plot([-kbx(t),kby(t),t=0..Pi/2],color=black):
kb[1]:=plot([ kbx(t),kby(t),t=0..Pi/2],color=black):
kb[2]:=plot([-kbx(t)+ex,-kby(t)+ey,t=0..Pi/2],color=black):
kb[3]:=plot([ kbx(t)+ex,-kby(t)+ey,t=0..Pi/2],color=black):
kb[4]:=plot([-kbx(t)+2*ex,kby(t),t=0..Pi/2],color=black):
kb[5]:=plot([ kbx(t)+2*ex,kby(t),t=0..Pi/2],color=black):
kb[6]:=plot([-kbx(t)+3*ex,-kby(t)+ey,t=0..Pi/2],color=black):
kb[7]:=plot([ kbx(t)+3*ex,-kby(t)+ey,t=0..Pi/2],color=black):

Ezeknek a vonalaknak az összeállításánál először célszerű színekkel megkülönböztetni az egyes darabokat, ezzel ellenőrizve, hogy azok valóban a helyükre kerültek-e.

> H:=display(seq({ka[i],kb[i]},i=0..7),insequence=false,scaling=constrained,linestyle=16):

> H;

A"látvány" kedvéért a felületet előállító n paramé

terrel kifejezett sokszögeket úgy színeztük, hogy azok állítsák elő a teljes színskálát.

> szin:= t->COLOR(RGB,cos(t)/2+0.5,
cos(t+evalf(4*Pi/3))/2+0.5,
cos(t+evalf(2*Pi/3))/2+0.5):

n: A beosztás finomságát jelenti

> n:=6:
f:=evalf(Pi/2/n):
# első nyolcad
for i from 0 to n do
A[n-i]:=[-kax(i*f),kay(i*f)]:
B[n-i]:=[-kbx(i*f),kby(i*f)]:
L[n-i]:=line(A[n-i],B[n-i],color=COLOR(HUE,(5*n-i)/8/n), linestyle=16);
od:

# második nyolcad
for i from n+1 to 2*n do
j:=i-n:
A[i]:=[kax(j*f),kay(j*f)]:
B[i]:=[kbx(j*f),kby(j*f)]:
L[i]:=line(A[i],B[i],color=COLOR(HUE,(4*n+i)/8/n), linestyle=16);

od:

# harmadik nyolcad
for i from 2*n+1 to 3*n do
j:=i-3*n:
A[i]:=[ex-kbx(j*f),ey-kby(j*f)]:
B[i]:=[ex-kax(j*f),ey-kay(j*f)]:
L[i]:=line(A[i],B[i], color=COLOR(HUE,(4*n+i)/8/n), linestyle=16);

od:


# negyedik nyolcad
for i from 3*n+1 to 4*n do
j:=i-3*n:
A[i]:=[ex+kbx(j*f),ey-kby(j*f)]:
B[i]:=[ex+kax(j*f),ey-kay(j*f)]:L[i]:=line(A[i],B[i], color=COLOR(HUE,(4*n+i)/8/n), linestyle=16);
od:

# második fele
for i from 4*n+1 to 8*n do
A[i]:=A[i-4*n]+[2*ex,0]:
B[i]:=B[i-4*n]+[2*ex,0]:
L[i]:=line(A[i],B[i], color=COLOR(HUE,(-4*n+i)/8/n), linestyle=16);

od:
V:=display(seq(L[i],i=0..8*n),insequence=false,scaling=constrained,axes=none):

>

> V;

> for i from 0 to 8*n-1 do
P[i]:=polygonplot([A[i],A[i+1],B[i+1],B[i]],color=COLOR(HUE,i/8/n)):
od:

> display(V,H,seq(P[i],i=0..8*n-1),insequence=false,axes=none,style=patchnogrid);

Annak, aki az itt előállított rajz alapján szeretné elkészíteni az alakzat modelljét (valamilyen keményebb papírra nyomtatva az oloid hálózatát), szüksége lehet arra, hogy egyszerre egy-egy negyedrésznyit, fagy felényit nyomtasson kia hálózatból:

> f1:= display( ka[0],kb[0],
kb[1],ka[1],
seq(L[i],i=0..2*n),
seq(P[i],i=0..2*n-1),
insequence=false,axes=none,style=patchnogrid):
f2:= display( ka[2],kb[2],
kb[3],ka[3],
seq(L[i],i=2*n..4*n),
seq(P[i],i=2*n..4*n-1),
insequence=false,axes=none,style=patchnogrid):
f3:= display( ka[4],kb[4],
kb[5],ka[5],
seq(L[i],i=4*n..6*n),
seq(P[i],i=4*n..6*n-1),
insequence=false,axes=none,style=patchnogrid):
f4:= display( ka[6],kb[6],
kb[7],ka[7],
seq(L[i],i=6*n..8*n),
seq(P[i],i=6*n..8*n-1),
insequence=false,axes=none,style=patchnogrid):

>

> f1;f2;f3;f4;

> display(f1,f2);
display(f3,f4);

>

Gurul-e az oloid?

> restart;

Az oloid modelljét elkészítve érdekesnek tűnő kérdést vethetünk fel: Gurítható-e?
Egy térgeometriai alakzatról akkor mondjuk, hogy "gurul" , ha egy síkon gördítve olyan mozgást végez, amely során a tömegközéppontjának egy síktól mért távolsága nem változik. Ezért gurul pl. a gömb minden irányba, a henger egyenes vonal mentén, a kúp egy körív mentén, stb.

Ha az oloid modelljét egy síklapú asztalon próbáljuk gördíteni, egy sajátos kacsázó mozgásnak lehetünk tanúi.
(Éppen a hálózatát követve mozog, amely - mint láttuk - periodikus.)
Mégis csak akkor mondhatjuk, hogy "gurul" az oloid, ha belátjuk, hogy bármely érintősíkja ugyanolyan távolságra van a tömegközéppontjától, amely jelen esetben a két kör középpontját összekötő szakasz felezőpontja.(A mi koordinátarendszerünkben az origó.)
A kérdés eldöntése céljából meghatároztuk az origónak a - tetszőleges - AB alkotóra eső merőleges vetületét:

Térjünk vissza az elején bevezetett függvényekhez, melyek az oloid alkotóit határozták meg:

> ax:= t -> 1/2+cos(t):
ay:= sin:
bx:= t-> 1/2*(cos(t)-1)/(cos(t)+1):
bz:= t-> sqrt((2*cos(t)+1))/(cos(t)+1):

> ax(t);ay(t);
bx(t);bz(t);

Legyen egy P=[px,py,pz] az AB szakasznak egy p paramétertől függő futópontja, ahol 0<p<1

> px:= t-> ax(t)+p*(bx(t)-ax(t)):
py:= t-> ay(t)+p*(0-ay(t)):
pz:= t-> 0+p*(bz(t)-0):

Ezek a függvények még tartalmazzák a p paramétert..

Felírjuk az AB és PO vektorok skalárszorzatát, melynek 0 -nak kell lennie akkor, ha azt a p értéket keressük, melyre OP merőleges AB -re.

> e:=(bx(t)-ax(t))*px(t)+(0-ay(t))*py(t)+(bz(t)-0)*pz(t)=0;

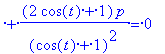
> p:=solve(e,p);

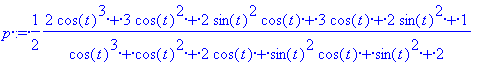
> simplify(p);

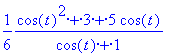
Most már a px,py,pz függvények kizárólag t függvényei:

> xp:=simplify(px(t));
yp:=simplify(py(t));
zp:=simplify(pz(t));

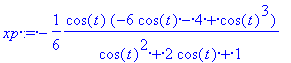
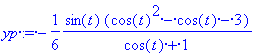
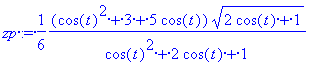
> d:= sqrt(xp^2+yp^2+zp^2);

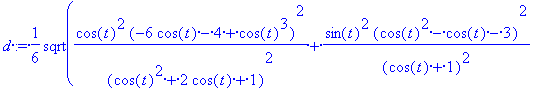
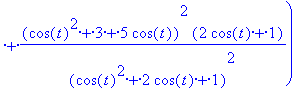
> d:= simplify(d);

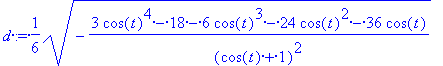
Úgy tűnik, ez nem egy konstans kifejezés, erről néhány rajzzal meg is győződhetünk.
Elegendő a [0,Pi/2] intervallumot vizsgálnunk.

> plot(d,t=0..Pi/2);

> plot([d,0*t],t=0..Pi/2,scaling=constrained);

> t:=0;d0:=simplify(d);unassign('t'):t;

A második rajzból jobban kitűnik, hogy a súlypontnak az érintősíktól mért távolsága nem túl tág határok között változik.

> t:=Pi/2; d1:=simplify(d);

> evalf(d0-d1);

Eredményünk tehát az, hogy az oloid nem gurul - de majdnem!

Az alkotókra merőleges felület:

Számolásunk melléktermékeként előállt a P[px(t),py(t),pz(t)] pont, amely egy adott t paraméter érték mellett az ehhez paraméterhez tartozó alkotóra az origóból bocsátott merőleges talppontja, ha azonban t - t a megfelelő értékek között változó paraméternek tekintjük, akkor egy térgörbét kapunk, melynek pontjai az említett talppontok.
Ha előállítjuk azt a kúpfelületet, amelynek csúcsa az origó, vezérgörbéje a [px(t),py(t),pz(t)] térgörbe, akkor egy olyan felülethez jutunk, amelyre az oloid minden alkotója merőleges.

Ezt a felületet fogjuk előállítani, mint vizsgálódásunk "melléktermékét".

> with(plots):with(plottools):

Warning, the name changecoords has been redefined

Először újra megadjuk a már ddig is megrajzolt alakzatainkat.

> n:=30:
a:=[seq( [ 1/2+cos(i*2*Pi/n),sin(i*2*Pi/n),0],i=1..n)]:
b:=[seq( [-1/2+cos(i*2*Pi/n),0,sin(i*2*Pi/n)],i=1..n)]:
CA:=polygonplot3d(a, color=yellow):
CB:=polygonplot3d(b,color=cyan):
RV:=polygonplot3d([a,b],linestyle=16,style=wireframe,color=blue):

> n:=12:
for i from 0 to n do
t:=i*Pi/n-Pi/2:
A[i]:=[ax(t),ay(t), 0]:
B[i]:=[bx(t), 0, bz(t)]:
L[i]:=line(A[i],B[i]
, color=COLOR(HUE,(4*n+i)/8/n)
):
od:
unassign('t'):

> V1:=display3d(seq(L[i],i=0..n),insequence=false,color=orange):
V2:=rotate(V1,Pi,0,0):
V3:=rotate(V1,Pi/2,0,Pi):
V4:=rotate(V2,Pi/2,0,Pi):

> PV1:=spacecurve([px(t),py(t),pz(t)],t=-Pi/2..Pi/2,color=magenta,linestyle=16):
PV2:=spacecurve([-px(t),pz(t),py(t)],t=-Pi/2..Pi/2,color=magenta,linestyle=16):
PV3:=spacecurve([px(t),py(t),-pz(t)],t=-Pi/2..Pi/2,color=magenta,linestyle=16):
PV4:=spacecurve([-px(t),-pz(t),py(t)],t=-Pi/2..Pi/2,color=magenta,linestyle=16):

> NS:= array(-1..4*n):
NS[-1]:=[0,0,0]:
for i from 0 to n do
t:=-Pi/2+i*Pi/n:
NS[i]:= [ px(t), py(t), pz(t)]:
NS[-i+2*n]:= [-px(t), pz(t), py(t)]:
NS[-i+3*n]:= [ px(t), py(t),-pz(t)]:
NS[i+3*n]:= [-px(t),-pz(t), py(t)]:
od:
NF:=polygonplot3d(NS,style=patchnogrid,scaling=constrained,lightmodel=light3):

Megjelenítések:

> display3d(CA,CB,RV,V1,V2,V3,V4,scaling= constrained);

> display3d(RV,V1,V2,V3,V4,PV1,PV2,PV3,PV4,scaling= constrained);

> display3d(RV,V1,V2,V3,V4,PV1,PV2,PV3,PV4,NF,scaling= constrained);

> display3d(
# CA,CB,RV,
# V1,V2,V3,V4,
# PV1,PV2,PV3,PV4,
NF,scaling= constrained);

>