hatb

A hat.mws Maple fájl forrásprogramja Ezt a programot a MAPLE konvertálta HTML formátumra (egy átlagos teljesítményû gépen mintegy fél órányi munkával).
A kész HTML fájlba csak ott javítottunk bele, ahol animációk vannak. Azért tettük ezt, hogy meggyorsítsuk a kapott html fájl betöltését és kezelését. A keletkezett animált gif fájlokra csak hivatkozunk, a szövegben egy-egy álló képpel helyettesítettük õket.

Hat tetraéderbõl álló mozgatható alakzat, egy kaleidociklus
Készítette: dr. Szilassi Lajos
SZTE JGYTF Matematika Tanszék
E-mail: szilassi@jgytf.u-szeged.hu

Feladat: Tekintsünk egy olyan tetraédert, melynek két szemközti éle merõleges egymásra., és normáltanszverzálisuk talppontjai e szemközti élek felezõpontjai. Legyen a merõleges oldalak - nevezzük õket alapél eknek - hossza 2a , távolságuk d ! Az a , és d szakaszok aránya - hasonlóságtól eltekintve - egyértelmûen meghatározza a tetraédert, melyet azzal is egyértelmûen megadhattunk volna, hogy lapjai csupa egybevágó egyenlõszárú háromszögek.

Illesszünk össze hat ilyen - megfelelõen méretezett - tetraédert az alapélei mentén úgy, hogy a szomszédos tetraéderek a közös alapéleik mentén elmozdulhassanak, csuklós szerkezetnek tekintve a közös alapélt. A hat tetraéder alkosson egy zárt láncot, vagyis az elsõ egyik alapélével a hatodikhoz csatlakozzék!
A hat tetraéder egy - az összeillesztett alapélek mentén - mozgatható konstrukciót alkot.
Azt a feladatot tûzzük ki célul, hogy ezt a mozgást leírjuk a MAPLE eszközeivel.

(A fenti rajz ennek az alakzatnak a mozgatható modellje. Ráklikkentve aktivizálódik a mozgást vezérlõ kezelõfelület.)

Az alakzat megadása

A feladat általános elemzése

A feltételeknek eleget tevõ papírmodellt - vagy a fenti mozgó modellt vizsgálva észrevehetjük, hogy két-két "szemközti" alapél egy síkban mozog, így ezeknek a mozgását leírva lényegében megadtuk az egész konstrukció mozgását.
A tetraéderek alapélei legyenek rendre A1B1 , P1Q1, A2B2, P2Q2, A3B3, P3,Q3 .
Az A1B1 alappal szemközti alapél a P2Q2 , amely kezdõ helyzetében éppen merõleges A1B1 -re, és innen indulva A1B1 -el ellentétes irányban forog.
Úgy adjuk meg az alakzat csúcspontjainak a koordinátáit, hogy ez a tulajdonság már a pontok koordinátáinak a megadásában is tükrözõdjék.

Jelentse f az A1B1 szakasznak az x tengellyel, g pedig a P2Q2 szakasz y tengellyel bezárt szögét! Így a kezdõ helyzetben f=g=0 .Az A1B1 szakasz felezõpontja legyen (x1,y,0) , a P2Q2 szakaszé (-x2,-y)
Az

xa:= x1 + a*cos(f): ya:= y - a*sin(f):
xb:= x1 - a*cos(f): yb:= y + a*sin(f):
xp:= - x2 + a*sin(g): yp:= -y - a*cos(g):
xq:= - x2 - a*sin(g): yq:= -y + a*cos(g):

változókat bevezetve az egy síkban mozgó négy pont koordinátáit az
A1:=[xa, ya, 0]:
B1:=[xb, yb, 0]:
P2:=[xp, yp, 0]:
Q2:=[xq, yq, 0]:
koordinátákkal írhatjuk le.
Az alakzatot meghatározó többi pontot ezekbõl a z tengely körüli 120°-os elforgatással kapjuk. Pl. a legelsõ A1 B1 P1 Q1 tetraéder további két csúcsa:
P1:=[-xp/2, yp, -xp*sqrt(3)/2]:
Q1:=[-xq/2, yq, -xq*sqrt(3)/2] :
Az (x1,y) pont azt a "pályát" írja le az xy síkban, amelyen az A1B1 szakasz felezõpontja mozog, (-x2,-y) pedig azt, amelyen a vele egy síkban lévõ P2Q2 felezõpontja. Azért elegendõ mindkét ponthoz ugyanazt az y értéket rendelnünk, mert lényegében csak a két pont y koordinátája közötti különbséget kell meghatároznunk. Ezzel biztosítjuk, hogy a mozgás közben az egész alakzat "tömegközéppontja" az origóban maradjon.

>

Az alakzat csúcspontjainak a meghatározása

> restart;with(plots):with(plottools):

Warning, the name changecoords has been redefined

Az alakzat pontjai között fennálló - a koordináták megválasztásában nem tükrözõdõ - kapcsolatok leírására gyakran szükségünk lesz végpontjai koordinátáival adott szakasz hosszának a felírására, valamint annak eldöntésére, hogy két szakasz (vektor) merõleges-e egymásra, ezért egy szakasz (vektor) hosszának a négyzetére, valamint két vektor skalárszorzatára bevezetünk egy-egy függvényt. Az utóbbit megoldhattuk volna a " l i nalg " programcsomag behívásával is, de emiatt az egy függvény miatt nem célszerû terhelnünk a programot, melyre feltehetõen így is sok számolás vár.)

> v:=array[1..3]:
w:=array[1..3]:
tn:= (v,w) -> (v[1]-w[1])^2+(v[2]-w[2])^2+(v[3]-w[3])^2:
s:= (v,w) ->v[1]*w[1]+v[2]*w[2]+v[3]*w[3]:

Az A1=(xa,ya,0), B1= (xb,yb,0), P2=(xp,yp,0) , Q2=(xq,yq,0) pontokkal fogjuk felírni az alakzat összes csúcsát.
Szükségünk lesz még az A1B1 , P1Q1 , A2,B2 , P2Q2 szakaszok felezõpontjaira.

> xa:= x1+a*cos(f): ya:= y-a*sin(f):
xb:= x1-a*cos(f): yb:= y+a*sin(f):
xp:=-x2+a*sin(g): yp:=-y-a*cos(g):
xq:=-x2-a*sin(g): yq:=-y+a*cos(g):
A1:=[xa,ya,0]:
B1:=[xb,yb,0]:
A2:=[-xa/2,ya,xa*sqrt(3)/2]:
B2:=[-xb/2,yb,xb*sqrt(3)/2]:
A3:=[-xa/2,ya, -xa*sqrt(3)/2]:
B3:=[-xb/2,yb, -xb*sqrt(3)/2]:

Megadjuk magának az alakzatnak a lapjait, tetraéderenként csoportosítva:

> T:=[[A1,B1,P1],[B1,A1,Q1],[A1,P1,Q1],[P1,B1,Q1],
[A2,B2,P1],[B2,A2,Q1],[A2,P1,Q1],[P1,B2,Q1],
[A2,B2,P2],[B2,A2,Q2],[A2,P2,Q2],[P2,B2,Q2],
[A3,B3,P2],[B3,A3,Q2],[A3,P2,Q2],[P2,B3,Q2],
[A3,B3,P3],[B3,A3,Q3],[A3,P3,Q3],[P3,B3,Q3],
[A1,B1,P3],[B1,A1,Q3],[A1,P3,Q3],[P3,B1,Q3]]:

>

Kontroll 1: Az alakzat így megadott koordinátáiból adódó összefüggések vizsgálata.

Lényegében azt vizsgáljuk, hogy amennyiben a fenti képletekkel adjuk meg az alakzat koordinátáit, azok jól tükrözik-e az ebbõl adódóan elvárható tulajdonságokat.

Elsõként írassuk ki a számoláshoz használt pontok koordinátáit:

> print(`
A1: `,A1,`
B1: `,B1,`
P2: `,P2,`
Q2: `,Q2,`
___________

`);
print(`
F1: `,F1,`
F2: `,simplify(F2),`
F3: `, simplify(F3),`
F4: `,F4,`
___________
`);

$`\n$

$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$

Ellenõrizhetjük, hogy az A1B1 és P1Q1 alapok valóban 2a hosszúak, f - tõl és g -tõl függetlenül.

> simplify(tn(A1,B1));simplify(tn(P1,Q1));
simplify(tn(A2,B2));simplify(tn(P2,Q2));

Mind a négy szakasz hossza - természetesen - 2a .

Megvizsgáljuk, - egyelõre g=f feltétel mellett - hogy az A1B1 és P2Q2 szakaszok valóban ellentétes irányban forognak-e merõleges kezdõ ( f=g=0 ) helyzetbõl indulva.

> x1:=15: x2:=15: y:=0:a:=10: g:=f:
k1:= circle([ x1,0], a, color=magenta):
k2:= circle([-x2,0], a, color=magenta):
rp:=90:e:=evalf(2*Pi/rp):
for i from 0 to rp do
f:=i*e:
F[i]:=line([xa,ya],[xb,yb], color=brown):
G[i]:=line([xp,yp],[xq,yq], color=blue):
od:
display(seq(display(G[i],F[i],k1,k2,insequence=false),i=0..rp),insequence=true,scaling= constrained,linestyle=16);

A sikeres kísérlet után fel kell oldanunk az ideiglenesen konkrét számokat jelentõ változókat ahhoz, hogy továbbra is általános paraméterekkel számolhassunk. Ezt késõbb is többször meg fogjuk tenni. Most ellenõrizzük is, hogy a pontjaink koordinátái a felszabadítás elõtt valóban számok, ezt követõen változók.

> print(`
A1: `,A1,`
B1: `,B1,`
P2: `,P2,`
Q2: `,Q2,`
___________

`);
unassign('x1','x2','y','a','f','g'):
print(`
A1: `,A1,`
B1: `,B1,`
P2: `,P2,`
Q2: `,Q2,`
___________

`);

$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$

$`\n$

Egy újabb - fiktív adatokkal felírt - kísérlettel vizsgáljuk meg, hogy ha az F1 , ill, F4 pont, amely körül forog az A1B1 , ill. P2Q2 szakasz maga is egy körön forogna, akkor ezzel mennyire írnánk le helyesen az alakzatot. Ennek a körnek az adatait nem teljesen önkéntesen választottuk. Megfigyelhetjük, hogy amíg az f (és g ) szög Pi/2 -nyit fordul, azalatt az F1 pont - és ugyanígy F4 is - egy 2d oldalú szabályos háromszög alapfelezõ pontjából egy csúcsába megy át (ill. fordítva). Ennek megfelelõen választottuk meg e kör középpontját és sugarát.

> a:=10:d:=a*sqrt(3):# d:=25:
r:=(d-d*sqrt(3)/3):
x1:=d-r*cos(2*f):
x2:=d+r*cos(2*f):
y:=r*sin(2*f):
g:=f:

> k1:= circle([d,0], r, color=red):
k2:= circle([-d,0], r, color=red):
pa:=plot([xa,ya,f=0..2*Pi],color=brown):
pp:=plot([xp,yp,f=0..2*Pi],color=blue):
rp:=90:e:=evalf(2*Pi/rp):
for i from 0 to rp do
f:=i*e:
F[i]:=line([xa,ya],[xb,yb], color=brown):
G[i]:=line([xp,yp],[xq,yq], color=blue):
unassign('f'):
od:
display(seq(display(G[i],F[i],k1,k2,pa,pp,insequence=false),i=0..rp),insequence=true,scaling= constrained,linestyle=16);

Ugyanezekkel a fiktív adatokkal adjuk meg és mozgassuk magát az alakzatot!

> rp:=90:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=polygonplot3d(T):
unassign('f'):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

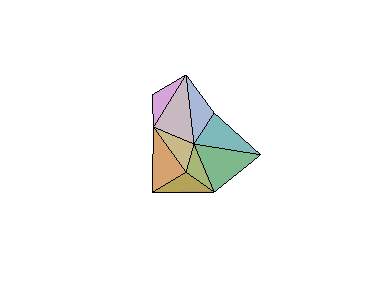
Javasoljuk olvasóinknak, hogy vizsgálják meg ugyanezt a mozgást más. pl a=10 ., b=25 , vagy a=10, b=15 paraméter-értékek mellett. Ebbõl ugyanis egyértelmûen kiderül, hogy rögzített a érték mellett a*sqrt(3) az a minimális d érték, amelynél még "nem akad meg" mozgás közben az alakzat. ha ennél kisebb d , akkor az alakzat olykor önátmetszõvé válik.

Eredményünkbõl egyelõre csak azt állapíthatjuk meg, hogy az alakzat koordinátáit és abból a lapjait helyesen írtuk fel, de alakzatunk csak "olyan" , mint amelyet meg szeretnénk konstruálni, de nem az, ugyanis az alakzat méretei nem konstansok. Errõl meggyõzõdhetünk azzal, hogy megvizsgáljuk, függ f-tõl pl.: az F1F2 szakasz hossza, melynek konstansnak kellene lennie.

> unassign('f');
df:=tn(F1,F2);

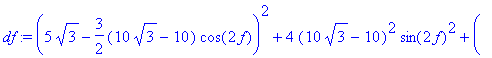
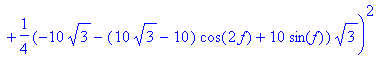
df := (5*sqrt(3)-3/2*(10*sqrt(3)-10)*cos(2*f))^2+4*...

> plot(df,f=0..2*Pi);

Ugyanígy annak is f tõl függetlenül teljesülnie kellene, hogy a tetraéderek alapjai merõlegesek egymásra.

> s(B1-A1,P1-Q1);

Egyelõre az sem teljesül, hogy a tetraéder két alapéle bármely f esetén merõleges egymásra.
Ezért szabadítsuk fel ismét változóinkat, és lássunk munkához.

> unassign('x1','x2','y','a','d','f','g'):
print(`
A1: `,A1,`
B1: `,B1,`
P2: `,P2,`
Q2: `,Q2,`
___________

`);

$`\n$

Kísérletünk azonban nem volt haszontalan. A késõbbi gyors és eredményes munka érdekében célszerû elsõként egy jó input -output rendszert kialakítani, és minden közbülsõ kontroll lehetõséget kihasználni, még akkor is, ha kiépítése olykor látszólag késlelteti a végeredmény gyors elérését.

>

Feladatunk olyan összefüggések feltárása lesz, melyek alapján az x1 , x2 és y változókat, majd ezek alapján az alakzat pontjainak koordinátáit felírjuk az a , d és f változók függvényeként, melyben a megjelenítés során a és d értéke egy-egy konkrét szám, f pedig 0 és 2*Pi között változó paraméter lesz.

Elsõ egyenlet:
Írjuk fel azt az összefüggést, amely biztosítja, hogy az A1B1 és P1Q1 alapok merõlegesek legyenek egymásra, azaz skalárszorzatuk nulla:

> e1:=s(B1-A1,P1-Q1)=0;

> m:=solve(e1,g);

> g:=arctan(2*tan(f));

Ez egy igen fontos összefüggés, alapos elemzést érdemel.

>

Kontroll 2: Az f és g változók közötti összefüggések elemzése.

> plot(g,f=0..2*Pi,scaling= constrained,color=red);

Láthatóan szakadási helye van a g és f közötti kapcsolatot kifejezõ függvénynek a Pi/2 és 3*Pi/2 helyen, így ez biztosan nem jól írja le a kapcsolatot. Kiküszöbölhetjük ezt a szakadást, ha a (Pi/2, 3*Pi/2) szakaszon megváltoztatjuk a függvény elõjelét:

> plot(signum(cos(f))*g,f=0..2*Pi,scaling= constrained,color=red);

Nekünk azonban g szinuszára és koszinuszára lesz szükségünk, így vizsgáljuk meg azokat:

> plot([sin(g),cos(g)],f=0..2*Pi,scaling= constrained,color=[red,blue]);

Látszik, hogy mindkét függvénynél ugyancsak szükség lesz ugyanarra az elõjel-korrekcióra:

> plot([signum(cos(f))*sin(g),signum(cos(f))*cos(g)],f=0..2*Pi,scaling= constrained,color=[red,blue]);

Eredményünket már akár használatra alkalmasnak is tekinthetnénk, azonban vizsgáljuk meg, nem lehet-e egyszerûbb alakra hozni ezeket a függvényeket.

Lényegében nem is a g -t, hanem annak szinuszát és koszinuszát kell kifejeznünk f -el.

> simplify(sin(g));
simplify(cos(g));

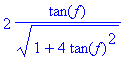
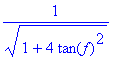
Itt célszerû "kézzel" beleavatkoznunk, a kapott törteket bõvítsük cos(x)-el, majd az így kapott kifejezésekre vezessünk be új változókat:

> sg:=simplify(2*sin(f)/sqrt(cos(f)^2+4*sin(f)^2));
cg:=simplify(cos(f)/(sqrt(cos(f)^2+4*sin(f)^2)));

>

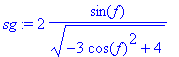
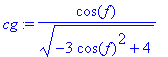
Kontroll3 : Az sg=sin(g) és cg=cos(g) helyettesítés vizsgálata

Az sg és cg változók lényegében a P2 és Q2 pontoknak az F4 pont körüli forgását írják le.

> plot([sg,cg],f=0..2*Pi,scaling= constrained,color=[red,blue]);
plot([sg,cg,f=0..2*Pi],scaling= constrained,color=[red,blue]);

Figyeljük meg, hogy a fenti két utasítás csak abban tér el egymástól, hogy másutt van benne a ] jel. Az elsõ képlet két függvényt ír le, melyek független változója f , a második pedig az ezek által meghatározott paraméteres alakban felírt síkgörbét. E két dolgot a késõbbiekben is gyakran fogjuk együtt szemlélni.

Eredményünk nem csak az, hogy lényegesen egyszerûbb alakban kaptuk meg a keresett összefüggéseket, hanem az is, hogy most már mindenütt folytonos és differenciálható függvények írják le az f és g közötti kapcsolatot, amelyet eredetileg az e1 egyenletben kaptunk:

> unassign('g'):simplify(e1/a^2/2);

> is(cos(f)*sg-2*sin(f)*cg=0);

Bár a kapott eredmény tökéletesen megnyugtató, az érdekesség kedvéért vizsgáljuk meg, hogy ha ugyanarról a pontról indulva egyezõ irányba forogna körbe az f és g szög, milyen lenne a kapcsolat közöttük.

> k:= circle([0,0], 1, color=red):
rp:=360:e:=evalf(2*Pi/rp):
for i from 0 to rp do
f:=i*e:
F[i]:=line([0,0],[cos(f),
sin(f)], color=brown):
G[i]:=line([0,0],[cg,sg], color=blue):
unassign('f');
od:
display(seq(display(G[i],F[i],k,insequence=false),i=0..rp),insequence=true,scaling= constrained,linestyle=16);

Figyeljük meg, hogy az egyenletes sebességgel forgó f (barna) szögszárhoz képest a g szög (kék) szára néha lassabban, néha gyorsabban forog, ahogy azt a g és f közötti kapcsolat megkívánta:

> g:=signum(cos(f))*arctan(2*tan(f));
plot(g,f=0..2*Pi,scaling= constrained,color=[red,blue]);

>

Az új, sg és cg változókat bevezetve újra kell definiálnunk a g -t paraméterként tartalmazó változókat és pontokat.

> xp:=-x2+a*sg; yp:=-y-a*cg;
xq:=-x2-a*sg; yq:=-y+a*cg;
P2:=[xp,yp,0]:
Q2:=[xq,yq,0]:
P1:=[-xp/2,yp,-xp*sqrt(3)/2]:
Q1:=[-xq/2,yq,-xq*sqrt(3)/2] :
P3:=[-xp/2,yp, xp*sqrt(3)/2]:
Q3:=[-xq/2,yq, xq*sqrt(3)/2] :
F2:=(P1+Q1)/2:
F4:=(P2+Q2)/2:
print(`
P1: `,P1,`
Q1: `,Q1,`
P2: `,P2,`
Q2: `,Q2,`
___________

`);

$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$
$`\n$

>

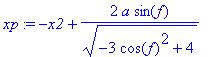
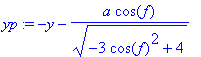
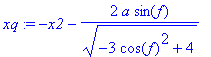
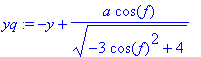
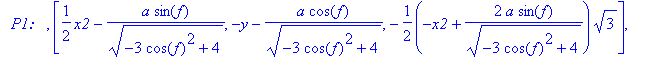
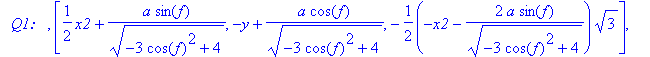
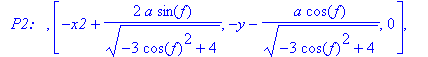
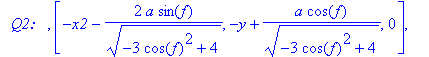
Második egyenlet:
A tetraéder egyértelmû megadásához az alapélei közötti távolságot, d - t vezettük be paraméterként. Ez ad lehetõséget arra, hogy kapcsolatot keressünk az x1 , x2 , és y változók között.

> e2:=tn(F1,F2)=d^2;

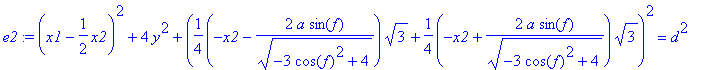
e2 := (x1-1/2*x2)^2+4*y^2+(1/4*(-x2-2*a*sin(f)/(sqr...

Ebbõl az egyenletbõl kifejezhetõ y :

> m2:=solve(e2,y);

> y:=m2[1];

Kiválasztottuk a pozitív gyököt., értékét átadva y -nak.

>

Kontroll 4: A tetraéder alapélei közötti kapcsolat vizsgálata.

Megvizsgáljuk, hogy az így kapott y érték mellett ugyanakkora-e az összes szomszédos alapélek felezõpontjai közötti távolság, valamint, hogy - a tan(g)=2*tan(f) összefüggésbõl adódóan - a szomszédos alapélek valóban merõlegesek-e egymásra.

> is(tn(F1,F2)=d^2);
is(tn(F2,F3)=d^2);
is(tn(F3,F4)=d^2);

> is(s(A1-B1,P1-Q1)=0);
is(s(P1-Q1,A2-B2)=0);
is(s(A2-B2,P2-Q2)=0);

Ez megnyugtató eredmény.

>

Harmadik egyenlet:
Eddig nem használtuk ki, hogy a tetraédereket csupa egyenlõszárú háromszögek alkotják.

> e3:=tn(A1,P1)=tn(A1,Q1);

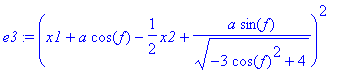
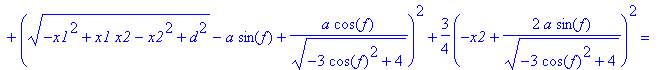
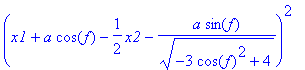
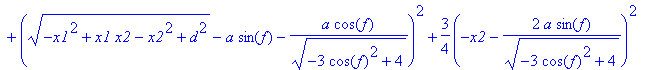
e3 := (x1+a*cos(f)-1/2*x2+a*sin(f)/(sqrt(-3*cos(f)^...

> m3:=solve(e3,x2):
simplify(m3[1]);
simplify(m3[2]);

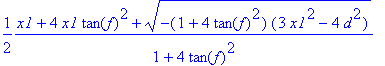
1/2*(x1+4*x1*tan(f)^2+sqrt(-(1+4*tan(f)^2)*(3*x1^2-...

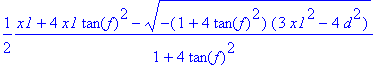
A szóba jöhetõ két gyök közül válasszuk ki a nagyobbat. Ha döntésünk helytelennek bizonyul, erre a pontra vissza kell térnünk.

Ismét élve egyszerûbb felírás lehetõségével az x2:=m3[1] helyettesítés helyett x2 -t fejezzük ki kissé elegánsabban:

> x2:=(x1+sqrt((4*d^2-3*x1^2)/(1+4*tan(f)^2)))/2;

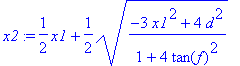
x2 := 1/2*x1+1/2*sqrt((-3*x1^2+4*d^2)/(1+4*tan(f)^2...

Itt egy kicsit segíteni kellett a MAPLE -nek. Ellenõrizzük , hogy jó- e az átírás:

> simplify(((m3[1]-x1/2)/(x2-x1/2))^2);

Nem a legegyszerûbb módját választottuk az ellenõrzésnek, de a MAPLE óvatosan bánik az egyszerûsítésekkel, néha kevésbé látja át, mint mi. (Néha viszont jobban.)

Ezt a behelyettesítést elvégezve y már csak x1 valamint a d és f paraméterek függvénye:

> print(` y =`,y);

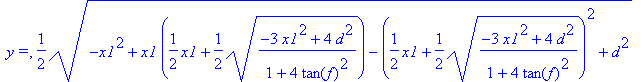
Negyedik egyenlet:
Használjuk ki, hogy az A1P1 szakasz kifejezhetõ d -vel és a -val. Hosszának négyzete a Pithagorasz tétel kétszeri alkalmazásából adódóan d^2 + 2 a^2 :

> e4:=simplify(tn(A1,P1))=d^2+2*a^2;

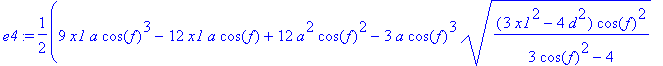
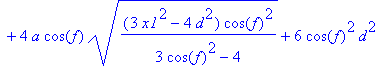
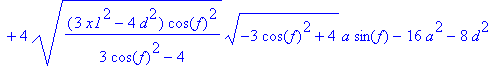
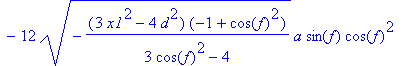
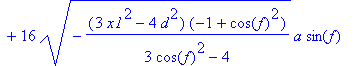
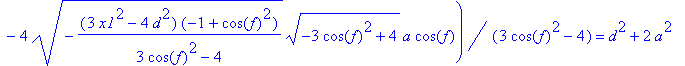
e4 := 1/2*(9*x1*a*cos(f)^3-12*x1*a*cos(f)+12*a^2*co...

> m4:=solve(e4,x1):

> simplify(m4[1]);
simplify(m4[2]);
simplify(m4[3]);
simplify(m4[4]);

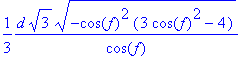
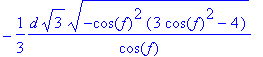
Az elsõ pillantásra ijesztõ megoldások közül (valamelyik) kettõ igen kellemes összefüggéssé szelídült, amit tovább egyszerûsíthetünk.

Itt hívjuk fel a figyelmet arra, hogy néha nem kapjuk meg m4[1] -ben a számunkra használható gyököt. Ugyanis e4 az x1 változóra nézve negyedfokú egyenlet, melynek a gyökeit az m vektor tetszõleges sorrendben tartalmazza, ígyvagy felírjuk mind a négyet, vagy "ki kell tapogatnunk", hogy ezek közül melyikre lesz szükségünk.

> x1:=1/3*d*sqrt(3)*sqrt((4-3*cos(f)^2));

> simplify(x2);
simplify(y);

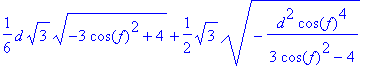
1/6*d*sqrt(3)*sqrt(-3*cos(f)^2+4)+1/2*sqrt(3)*sqrt(...

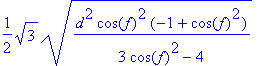
1/2*sqrt(3)*sqrt(d^2*cos(f)^2*(-1+cos(f)^2)/(3*cos(...

Bár már megkaptuk az x1 , x2 és y változókat a kívánt paraméterekkel kifejezve, eredményeinket írjuk fel újból, minél egyszerûbb és könnyebben kezelhetõ formában.

Itt nem könnyû észrevenni az egyszerûsítési lehetõséget. (A MAPLE nem vette észre.) Mi azonban észrevehetjük:

> simplify(x1*x2/(2*d^2/3));

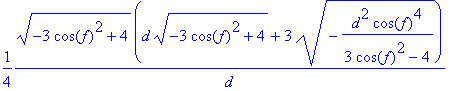
1/4*sqrt(-3*cos(f)^2+4)*(d*sqrt(-3*cos(f)^2+4)+3*sq...

Ebbõl az alakból - számunkra - már látszik, hogy x1*x2=2*d^2/3 Ezért célszerû x2 -t így definiálnunk:

> x2:=2*d*sqrt(3)/sqrt(-3*cos(f)^2+4)/3;

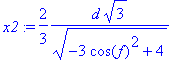
y -t ugyancsak felírhatjuk egyszerûbb alakban:

> y:=d*sqrt(3)*sin(f)*cos(f)/2/sqrt(-3*cos(f)^2+4);

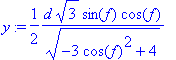
Bár ezekkel az új definíciókkal újra definiáltuk a pontok koordinátáit is, azonban hasznos lehet újból megadni õket, kihasználva a kínálkozó egyszerûsítési lehetõségeket, melyeket részben a MAPLE részben mi végezhetünk el "kézzel":

> simplify(xa);

> xa:=1/3*d*sqrt(3)*sqrt(-3*cos(f)^2+4)+a*cos(f);

> simplify(ya);

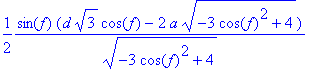
1/2*sin(f)*(d*sqrt(3)*cos(f)-2*a*sqrt(-3*cos(f)^2+4...

> ya:=1/2*sin(f)*(d*sqrt(3)*cos(f))/(sqrt(-3*cos(f)^2+4))-a*sin(f);

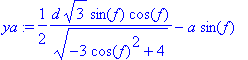
> simplify(xb);

> xb:=1/3*d*sqrt(3)*sqrt(-3*cos(f)^2+4)-a*cos(f);

> simplify(yb);

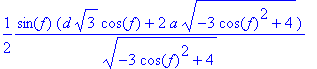
> yb:=1/2*sin(f)*(d*sqrt(3)*cos(f))/(sqrt(-3*cos(f)^2+4))+a*sin(f);

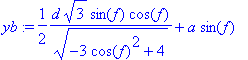
> simplify(xp);

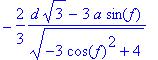
> xp:=2/3*(-d*sqrt(3)+3*a*sin(f))/(sqrt(-3*cos(f)^2+4));

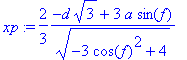
> simplify(yp);

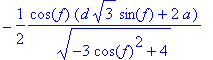
> yp:=-1/2*cos(f)*(d*sqrt(3)*sin(f)+2*a)/(sqrt(-3*cos(f)^2+4));

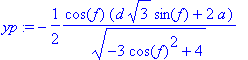
> simplify(xq);

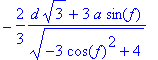
> xq:=-2/3*(d*sqrt(3)+3*a*sin(f))/(sqrt(-3*cos(f)^2+4));

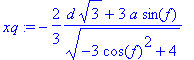
> simplify(yq);

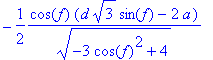
> yq:=-1/2*cos(f)*(d*sqrt(3)*sin(f)-2*a)/(sqrt(-3*cos(f)^2+4));

>

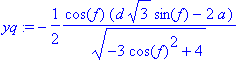
Ezzel lényegében befejeztük az alakzat pontjainak a megadását, már csak egy alaposabb ellenõrzésre van szükség

>

Kontroll 5: Az A1, B1, P1, Q1 pontok pályájának a vizsgálata.

Elõször minden pályát megvizsgálunk olyan konkrét paraméter érték mellett, amelyben a kezdõ (f=0) helyzetben az A1,A2 és A3 pontok éppen az origóba kerülnek.
Javasoljuk más paraméter értékekkel is ennek a vizsgálatnak az elvégzését. (Pl legyen az újabb vizsgálatban a=10 , d=25 .)

> a:=10; d:=10*sqrt(3); # d:=25;

> plot([x1,y],f=0..2*Pi,color=[red,blue]);
p1:=plot([x1,y,f=0..2*Pi],color=red):
plot([-x2,-y],f=0..2*Pi,color=[red,blue]);
p2:=plot([-x2,y,f=0..2*Pi],color=magenta):
display(p1,p2,scaling= constrained);

Bár az F1(x1,y) és F4(-x2,-y) pontokat különbözõ képletek írják le, - ez grafikonjaikon is tükrözõdik - egybevágó pályákat írnak le. Ugyanennek kell teljesülnie az A1,B1, P2,Q2 pontok pályáira is. Ellenõrzésképpen mind a négyet megjelenítjük, a B1 és Q2 pályáját kissé eltolva, hiszen ezeknek ugyanoda kellene esniük, mint az A1 , ill. P2 pályája.

> plot([xa,ya],f=0..2*Pi,color=[red,blue]);
pa:=plot([xa,ya,f=0..2*Pi],color=brown):
plot([xb,yb],f=0..2*Pi,color=[red,blue]);
pb:=plot([xb+5,yb+5,f=0..2*Pi],color=gold):
plot([xp,yp],f=0..2*Pi,color=[red,blue]);
pp:=plot([xp,yp,f=0..2*Pi],color=blue):
plot([xq,yq],f=0..2*Pi,color=[red,blue]);
pq:=plot([xq-5,yq-5,f=0..2*Pi],color=navy):

> display(p1,p2,pa,pb,pp,pq,scaling= constrained,linestyle=16);

Az eredményekkel elégedettek lehetünk, azonban vizsgáljuk meg magának az A1B1 és P2Q2 szakasznak a mozgását is!

> unassign('f'):
A:=[xa,ya]: B:=[xb,yb]:P:=[xp,yp]:Q:=[xq,yq]:
K:=(A+B)/2:H:=(P+Q)/2:
rp:=180:e:=evalf(2*Pi/rp):
for i from 0 to rp do
f:=i*e:
AB[i]:=line(A,B, color=brown):
PQ[i]:=line(P,Q, color=blue):
R[i] :=line(K,H, color=aquamarine):
unassign('f'):
od:
display(seq(display(AB[i],PQ[i],R[i],pa,pp,p1,p2, insequence=false),i=0..rp),insequence=true,scaling= constrained,linestyle=16);

A fenti animációból az sejthetõ, hogy az itt megfigyelt A1B1 és P2Q2 szakaszok felezõpontjainak a távolsága állandó. Vizsgáljuk meg ezt a sejtést:

> unassign('a','d','f'):
simplify(tn((A1+B1)/2,(P2+Q2)/2));

Valóban ennek a szakasznak a hossza d*sqrt(3). Lehetséges, hogy ezt kihasználva egyszerûbben megkaphattuk volna a fenti összefüggéseinket. Az eredmény azonban a feladat egyértelmû voltából adódóan ugyanez lett volna.

Mielõtt megjelenítenénk az alakzatunkat, - megszabadulva paramétereink konkrét értékétõl - próbáljuk meg algebrailag is ellenõrizni számításaink helyességét.

> unassign('a','d','f'):

>

K ontroll 6 : A tetraéderek élhosszainak a kiszámítása.

Vizsgálódásunknak egyetlen célja van: az, hogy a kapott tetraéder-élek megfelelõ hosszúak-e, vagyis igaz-e, hogy az alapok hosszának a négyzete 4*a^2 , a száraké d ^ 2+2*a^2 .

Az alaélek hossza:

> print(`
A1-B1 = `,simplify(tn(A1,B1)),`
P1-Q1 = `,simplify(tn(P1,Q1)),`
A2-B2 = `,simplify(tn(A2,B2)),`
P2-Q2 = `,simplify(tn(P2,Q2)));

A1-Q1 = `,simplify(tn(A1,Q1)),`
B1-P1 = `,simplify(tn(B1,P1)),`
B1-Q1 = `,simplify(tn(B1,Q1)),`
A2-P1 = `,simplify(tn(A2,P1)),`
A2-Q1 = `,simplify(tn(A2,P1)),`
B2-P1 = `,simplify(tn(B2,P1)),`
B2-Q1 = `,simplify(tn(B2,P1)),`
A2-P2 = `,simplify(tn(A2,P2)),`
A2-Q2 = `,simplify(tn(A2,Q2)),`
B2-P2 = `,simplify(tn(B2,P2)),`
B2-Q2 = `,simplify(tn(B2,Q2)));

$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$
$`\nA1-P1$

A további három tetraéder adatainak a megvizsgálása felesleges, hiszen azokat az elsõ háromnak az xy síkra vonatkozó tükrözésével kaptuk.

>

Kontroll 7 : A kapott alakzat elsõ megjelenítése.

A már kiszámíított koordináta-értékekkel úból megadjuk a poliédert jelentõ T mátrixot.

> A1:=[xa,ya,0]:
B1:=[xb,yb,0]:
A2:=[-xa/2,ya,xa*sqrt(3)/2]:
B2:=[-xb/2,yb,xb*sqrt(3)/2]:
A3:=[-xa/2,ya, -xa*sqrt(3)/2]:
B3:=[-xb/2,yb, -xb*sqrt(3)/2]:

P2:=[xp,yp,0]:
Q2:=[xq,yq,0]:
P1:=[-xp/2,yp,-xp*sqrt(3)/2]:
Q1:=[-xq/2,yq,-xq*sqrt(3)/2] :
P3:=[-xp/2,yp, xp*sqrt(3)/2]:
Q3:=[-xq/2,yq, xq*sqrt(3)/2] :
T:=[[[A1,B1,P1],[B1,A1,Q1],[A1,P1,Q1],[P1,B1,Q1]],
[[A2,B2,P1],[B2,A2,Q1],[A2,P1,Q1],[P1,B2,Q1]],
[[A2,B2,P2],[B2,A2,Q2],[A2,P2,Q2],[P2,B2,Q2]],
[[A3,B3,P2],[B3,A3,Q2],[A3,P2,Q2],[P2,B3,Q2]],
[[A3,B3,P3],[B3,A3,Q3],[A3,P3,Q3],[P3,B3,Q3]],
[[A1,B1,P3],[B1,A1,Q3],[A1,P3,Q3],[P3,B1,Q3]]]:

A megjelenítés során mindenképpen numerikus értékekkel kell dolgoznunk, ezért lényegesen lerövidítjük a számolást, ha a lépésközt ( e ) a processzor aritmetikáját használva tizedes törtként számítjuk ki.

> a:=10: d:=10*sqrt(3):
rp:=90:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=polygonplot3d(T):
unassign('f'):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

Az így elkészült alakzat további vizsgálatához már nem lesz szükség a fenti számításokra, melyeket egyelõre még "fejben tart" a MAPLE, ezért mentsük át eredményeinket a következõ programrészletbe (vagy egy új MAPLE fájlba) és kezdjük elölrõl a munkát, immár csak a rajzokra, animációkra koncentrálva.

>

Az alakzat megjelenítése
(Akit csak a végeredmény érdekel, ezt a részt az elõzõektõl függetlenül is futtathatja.)

> restart; with(plots):

Warning, the name changecoords has been redefined

> xa:=1/3*d*sqrt(3)*sqrt(-3*cos(f)^2+4)+a*cos(f):
ya:=1/2*sin(f)*(d*sqrt(3)*cos(f))/(sqrt(-3*cos(f)^2+4))-a*sin(f):
xb:=1/3*d*sqrt(3)*sqrt(-3*cos(f)^2+4)-a*cos(f):
yb:=1/2*sin(f)*(d*sqrt(3)*cos(f))/(sqrt(-3*cos(f)^2+4))+a*sin(f):
xp:=2/3*(-d*sqrt(3)+3*a*sin(f))/(sqrt(-3*cos(f)^2+4)):
yp:=-1/2*cos(f)*(d*sqrt(3)*sin(f)+2*a)/(sqrt(-3*cos(f)^2+4)):
xq:=-2/3*(d*sqrt(3)+3*a*sin(f))/(sqrt(-3*cos(f)^2+4)):
yq:=-1/2*cos(f)*(d*sqrt(3)*sin(f)-2*a)/(sqrt(-3*cos(f)^2+4)):
A1:=[xa,ya,0]:
B1:=[xb,yb,0]:
A2:=[-xa/2,ya,xa*sqrt(3)/2]:
B2:=[-xb/2,yb,xb*sqrt(3)/2]:
A3:=[-xa/2,ya, -xa*sqrt(3)/2]:
B3:=[-xb/2,yb, -xb*sqrt(3)/2]:

>

A hat tetraéder együtt, és külön-külön

Az alakzat lapjait tetraéderenként adjuk meg, ezzel elérhetjük, hogy ne az összes jelenjen meg a rajzon.

> T:=[[[A1,B1,P1],[B1,A1,Q1],[A1,P1,Q1],[P1,B1,Q1]],
[[A2,B2,P1],[B2,A2,Q1],[A2,P1,Q1],[P1,B2,Q1]],
[[A2,B2,P2],[B2,A2,Q2],[A2,P2,Q2],[P2,B2,Q2]],
[[A3,B3,P2],[B3,A3,Q2],[A3,P2,Q2],[P2,B3,Q2]],
[[A3,B3,P3],[B3,A3,Q3],[A3,P3,Q3],[P3,B3,Q3]],
[[A1,B1,P3],[B1,A1,Q3],[A1,P3,Q3],[P3,B1,Q3]]]:

1. Az alakzat, a MAPLE színeit használva:

Megengedhetjük, hogy a "kezdõ helyzet ne f=0-ról induljon, hanem bárhonnan. (Jelen esetben Pi/4 -tõl indul.)

> unassign('a','d','f'): a:=10:d:=10*sqrt(3):
rp:=90: e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e+Pi/4:
R[k]:=polygonplot3d(T):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

Megjegyezzük, hogy a "mozgás" finomságát - egyben sebességét - egyedül rp értéke határozza meg. Nagyobb teljesítményû gépeken célszerû legalább 100 -ra átállítani. Azonban ha animált gif fájlt készítünk a jelenetbõl, számítanunk kell azzal, hogy a fájl rp darab képbõl áll össze, így a mérete igen nagy lehet.

>

2. Színezzük a tetraédereket más-más színûre. Egyúttal megmutatjuk, hogy - mivel tetraédereink tengelyesen szimmetrikusak - lényegében elegendõ az f paramétert a (0,Pi) intervallumon végigfuttatni, az animációt folyamatos megjelenítésre állítva ugyanolyan mozzanatokat látunk, mint ha f a (0, 2Pi) intervallumon futna végig.

> unassign('a','d','f'):a:=10:d:=a*sqrt(3):
rp:=40:e:=evalhf(Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(seq(polygonplot3d(T[i],
color=szin[i]),i=1..6),insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained);

>

3. Érdekes mozgást figyelhetünk meg, ha csak minden második tetraédert jelenítjük meg:

> unassign('a','d','f'):a:=10:d:=10*sqrt(3):
rp:=100:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(seq(polygonplot3d(T[2*i]),i=1..3),
insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

>

4. Ugyancsak figyelemre méltó "jelenség", hogy az egymással szemközti tetraéderek egymásnak síkra vonatkozó tükörképei, ezért beállítható a nézõpont úgy, hogy a mozgás közben egyik tetraéder éppen eltakarja a másikat:

> unassign('a','d','f'):a:=10:d:=10*sqrt(3):
rp:=40:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(seq(polygonplot3d(T[3*i],
color=szin[i]),i=1..2),insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[0,120],axes=normal);

Ez persze nem meglepõ, az alakzat konstrukciójából egyértelmûen adódik. Pl. a 2 . és 5 . tetraéderek szimmetriasíkja az (xy) sík Egyúttal példát látunk arra, hogy miként konstruálhatunk olyan alakzatokat is, amelyben a tetraéderek nem érintik az origót:

> unassign('a','d','f'):a:=10:d:=25:
rp:=40:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(seq(polygonplot3d(T[3*i-1],
color=szin[i]),i=1..2),insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[90,0],axes=normal);

>

5. A "vicc kedvéért" változtassuk mozgás közben a tetraéder alapját 0 és a maximális érték között:

> unassign('a','d','f'):d:=10*sqrt(3):
rp:=40:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e: a:=5-5*cos(k*e):
R[k]:=display3d(seq(polygonplot3d(T[i]),i=1..6),
insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

A további kísérletezést olvasóinkra bízzuk.

>

Három szomszédos tetraéder mozgása
(Az alakzatot meghatározó élek pályájának a megfigyelése)

Megrajzoljuk a térben azokat az útvonalakat, amelyek mentén az A1B1 ill. a P2Q2 szakaszok felezõpontjai, ill. végpontjai mozognak, majd bemutatjuk az elsõ három tetraéder mozgását. A jobb áttekinthetõség kedvéért kialakíthatjuk úgy a konstrukciót, hogy az elsõ és harmadik tetraédernek csak az élváza, vagy két-két lapja legyen látható. Javasoljuk olvasóinknak, hogy próbálják ki mindkét "jelenetet".

> unassign('a','d','f'): a:=10:d:=10*sqrt(3):
#M:=[[[A1,B1],[A1,Q1],[A1,P1],[B1,Q1],[B1,P1]],
# [[P2,Q2],[P2,A2],[P2,B2],[Q2,A2],[Q2,B2]],
#[[A2,B2,P1],[B2,A2,Q1],[A2,P1,Q1],[P1,B2,Q1]]]:
M:=[[[A1,B1,P1],[A1,B1,Q1]],
[[P2,Q2,A2],[P2,Q2,B2]],
[[A2,B2,P1],[B2,A2,Q1],[A2,P1,Q1],[P1,B2,Q1]]]:

> AB:=spacecurve(A1, f=0..2*Pi, color=blue,linestyle=16):
PQ:=spacecurve(P2, f=0..2*Pi, color=blue,linestyle=16):
FAB:=spacecurve((A1+B1)/2, f=0..2*Pi, color=red,linestyle=16):
FPQ:=spacecurve((P2+Q2)/2, f=0..2*Pi, color=red,linestyle=16):
ut:=display3d({AB,PQ,FAB,FPQ}):

> rp:=100:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(ut,seq(polygonplot3d(M[i]
),i=1..3),insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling=constrained,axes=normal,orientation=[100,70]);

Javasoljuk olvasóinknak, hogy futtassák újra ezt a programrészletet pl. a=10 , d=30 , vagy bármilyen más paraméter értékkel. Ezzel válik igazán szemléletessé a konstrukció.

>

A tetraéderek lapjait más-más színnel színezzük:

Aki (pl. papírból) elkészíti ennek a mozgó alakzatnak a modelljét, érdekes modellt állíthat elõ azzal, hogy az egymáshoz illõ lapokra egy-egy - lényegében három rombuszból álló - képet applikál. Ezek a képek ugyanis az egyik oldalról nézve állnak csak helyesen, az ellenkezõ oldalról szemlélve olyannak látjuk, mint ha a képet alkotó rombuszokat rossz sorrendbe raktuk volna össze egy képpé. Ehhez a munkához nyújt segítséget ez a "jelenet":

> unassign('a','d','f'):
S:=[[[A1,B1,P1],[A2,B2,P1],[A2,B2,P2],
[A3,B3,P2],[A3,B3,P3],[A1,B1,P3]],
[[B1,A1,Q1],[B2,A2,Q1],[B2,A2,Q2],
[B3,A3,Q2],[B3,A3,Q3],[B1,A1,Q3]],
[[A1,P1,Q1],[A2,P1,Q1],[A2,P2,Q2],
[A3,P2,Q2],[A3,P3,Q3],[A1,P3,Q3]],
[[P1,B1,Q1],[P1,B2,Q1],[P2,B2,Q2],
[P2,B3,Q2],[P3,B3,Q3],[P3,B1,Q3]]]:

> a:=10:d:=10*sqrt(3):
rp:=90:e:=evalhf(2*Pi/rp):
for k from 0 to rp do
f:=k*e:
R[k]:=display3d(seq(polygonplot3d(S[i],color=szin[i]),i=1..4),
insequence= false):
od:
display3d(seq(R[k],k=0..rp),insequence=true,scaling= constrained,orientation=[50,120]);

>