Az eredeti probléma, amelyet Fibonacci kutatott (1202) arról szólt, hogy ideális körülmények között a nyulak milyen gyorsan, milyen rendszerességgel ellenek.

Tegyük fel, hogy egy mezõn él egy újszülött nyúl pár, egy hím és egy nõstény. A nyulak egy hónapos korukra lesznek ivarérettek, így a második hónap végén már megszülethetnek az elsõ kicsinyek.

Tegyük fel, hogy a mi nyulaink soha nem halnak meg és hogy a nõstények mindig új párt ellenek ( 1 hímet és 1 nõstényt) minden hónapban, a második hónaptól kezdve.

Fibonacci problémája: hány pár lesz egy éven belül?

1. Az elsõ hónap végén még csak 1 pár van.
2. A második hónap végén születik 1 új pár, így most már 2 pár van.
3. A harmadik hónap végén az eredeti nõsténynek születik a második pár nyula, így már 3 pár lesz.
4. A negyedik hónap végén az eredeti nõsténynek lesz újabb kicsinye, a második hónapban született nõstény most elli az elsõ kicsinyeit, így összesen már 5 pár nyúl van.
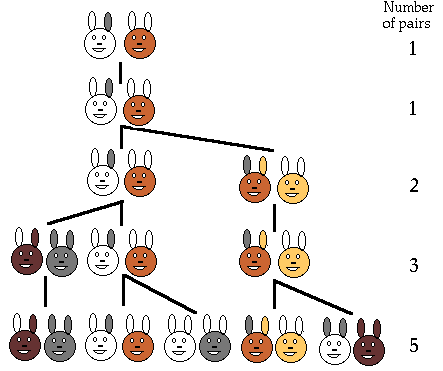
A párok száma

Minden hónap elején a nyúlpárok száma: 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Hogyan folytatódik a sorozat?

Megoldás

Miért ez a válasz a "nyúl-problémára"? Miért egyeznek meg a Fibonacci számok a nyúlpárok számával minden hónapban?

Hogyan lehet még szemléltetni a Fibonacci számokat?

Rajzoljunk két 1 egységnyi oldalú négyzetet egymás mellé, melyeknek egyik oldaluk érinti egymást. Ezek fölé kétegységnyi oldalhosszúságú négyzetet (2=1+1).

Ezután folytathatjuk a 3 egységnyi oldalhosszúságúval, amely az elõzõt érinti...

Ezt így folytathatjuk tovább. Minden oldalhosszúság az elõzõ 2 összegével egyezik meg. Ezen négyszögeknek az oldalhosszúságai Fibonacci számok, ezért ezeket Fibonacci négyszögeknek nevezzük.

A következõ ábra megmutatja, hogy hogyan lehet negyed körívekbõl spirált rajzolni úgy, hogy minden négyzetben egy negyed körív legyen.

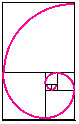Ezt Fibonacci spirálnak nevezzük.

Hasonló alakzatok a természetben is megjelennek csigaházakon, kagylókon:

A fenyõ tobozain is felfedezhetõ a Fibonacci spirál:

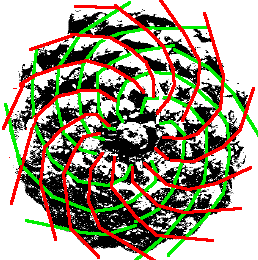A piros vonalak mutatják az egyik irányt, a zöldek a másikat.

A Fibonacci számok a természet ezernyi területén megjelennek, mint például növények leveleinek elrendezésében a száron, aztán a virágok szirmainak száma is Fibonacci szám.

Nézd meg a saját kezed!

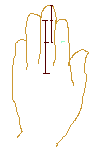
2 kezed van, mindkettõn...

5 ujj, ezeken...

3 ujjperc...

Mindez véletlen lenne csupán?????

Összeállította:

Herold Zsuzsa