![]()
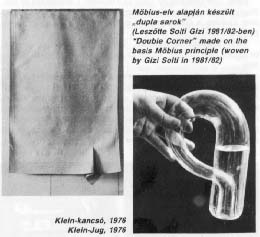
A Klein-kancsó

Azt kérdezed, hogy mi ez?
A válasz: egy palack, amibe semmit sem lehet tölteni!
Hogy egy kicsit tudományosabb megfogalmazással éljek:
a Klein-féle palack klasszkus példa az egyoldalú zárt
felületre. Ennek elõállítása a következõ:
egy lyukas hengerpalást-felületbõl indulunk ki. Ezt
deformáljuk, majd az alsó végét bevezetjük
a csõ belsejébe. Közben megnyújtjuk, majd kivezetjük
a lyukon keresztül. Ezután a csõ végét
hozzáforrasztjuk a hengerpaládt felsõ határgörbéjéhez,
végül a lyukat beforrasztjuk egy elemi felülettel.
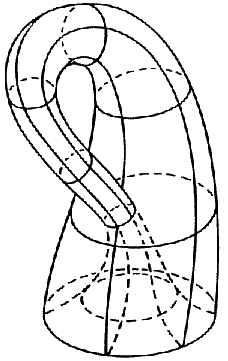
Így valóban egyoldalú felületet kapunk: hiszen a "csõ" segítségével be tudtunk jutni kívülrõl a kancsó belsejébe. De térben ezt nem tudjuk megvalósítani, hiszen az utolsó lépésként hozzáforrasztott elemi felület nyilvánvalóan metszi a csövet, holott ez az elvi eljárás alapján nem érintkezhetne vele.
Hogyan lesz egy négyzetbõl Klein-kancsó:
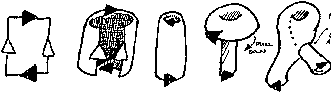

A Klein-kancsóról az is elmondható, hogy homeomorf két Möbius-szalag összeforgatásával:
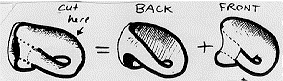
A Klein-kancsó Euler-karakterisztikája 0 (k=0), az összfüggõségi száma pedig 3 (n=3).
Hogyan lesz a tóruszból Klein-kancsó?
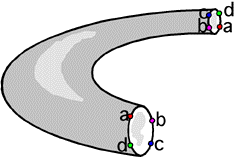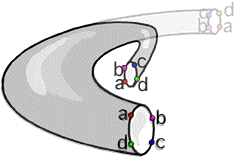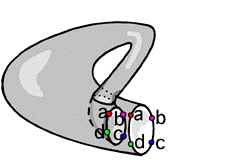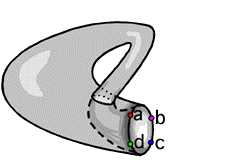
Nézzünk néhány képet a Klein-kancsóról!
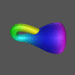



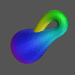
A következõ 3 kép a Klein-kancsó belsõ
felépítésérõl fed fel néhány
részletet:
Akik nem elégednek meg az álló képekkel, azoknak néhány mpeg movie!
Aki még a paraméteres egyenletre is kíváncsi...
Egy kis történelem!
A Klein-kancsó Felix Christian Kleinrõl kapta a nevét, aki 1849. április 25-én született Düsseldorfban, Poroszországban ( a mai Németországban ). Biography in English
Klein a nem-euklideszi geometriai munkásságáért volt különösen elismert, de ne feledkezzünk meg a topológiai vizsgálatairól sem, hiszen többek között neki köszönhetõ a Klein-kancsó, mely oly sok embert foglalkoztat napjainkban.
Egyéb mûvészi alkotásokat is ihletett a Klein-kancsó:
Szükségesnek vélem még megemlíteni, hogy a speciálkollégiumunk vezetõje is mutatott néhány dolgot a Klein-kancsóval kapcsolatban. Ime!
Végezetül, de nem utolsó sorban néhány egyéb "Klein-palackos" link:
Ha levelezni szeretnél:


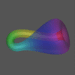

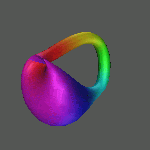
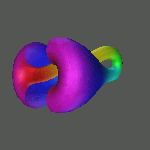

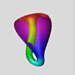


.gif)