
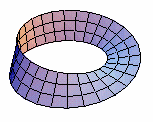
The Möbius Strip is a half-twisted band.
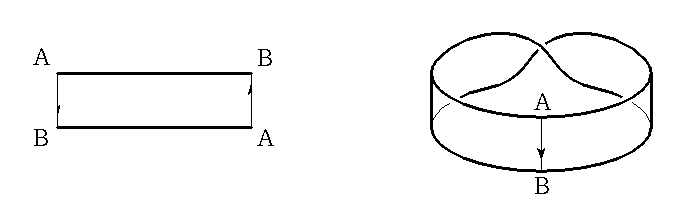
You can make one by taking a long thin strip of paper and attaching the two short ends together A Möbius band is a strip with a half-twist so that the top of one is at the bottom of the other:
In mathematical language:
1. Start with a long rectangle (ABCD) made of paper.
2. Give the rectangle a half twist.
3. Join the ends so that A is matched with D and B is matched with C.
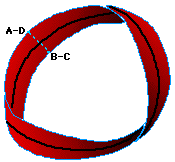
This curious surface is called a Möbius Strip or Möbius Band,
named after August Ferdinand Möbius, a nineteenth
century German mathematician and astronomer, who was a pioneer in the field
of topology. Möbius, along with his better known contemporaries, Riemann,
Lobachevsky and Bolyai, created a non-Euclidean revolution in geometry.
Möbius strips have found a number of surprising applications that exploit a remarkable property they possess: one-sidedness. Joining A to C and B to D (no half twist) would produce a simple belt-shaped loop with two sides and two edges -- impossible to travel from one side to the other without crossing an edge. But, as a result of the half twist, the Möbius Strip has only one side and one edge!
To demonstrate this, (1)start midway between the "edges" of a Möbius Strip and draw a line down its center; continue the line until you return to your starting point. Did you ever cross an edge? (2) Next, hold the edge of a Möbius Strip against the tip of a felt-tipped highlighter pen. Color the edge of the Möbius Strip by holding the highlighter still and just rotating the Mobius Strip around. Were you able to color the entire edge? (3) Now, with scissors cut the Mobius Strip along the center line that you drew. Then draw a center line around the resulting band, and cut along it. Did you predict what would happen?

A Möbius band has a single boundary curve, and only one side. It is non-orientable, which means that it contains a path for which it is impossible to define a left- and right-hand side in a consistent global way. In fact, it is the fundamental unit of non-orientability in that any non-orientable surface contains a Möbius band.
A Möbius band can not be embedded in the plane.
The parametric equations for the Mobius Band are: A Möbiusz szalag paraméteres képlete:
f(u, v) = ( (cos(u) + v*cos(u/2)*cos(u)), (sin(u) +v*cos(u/2)*sin(u)), v*sin(u/2)),
0 <= u <= 2*pi, -0.3 <= v <= 0.3
source: Alfred Gray, Modern Differential Geometry of Curves and Surfaces
What they have used for:



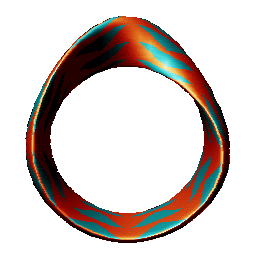
Of course, this is not a complete work , this is just a frame to direct your intrest on the beuties of Geometry.
If any remarks mail me: