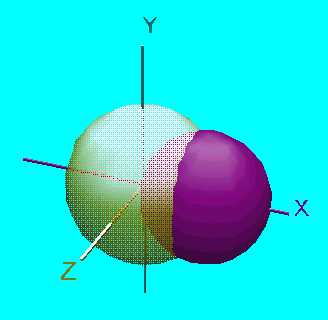
Egy egységnyi sugarú S gömb középpontja illeszkedik egy másik, G gömb felületére. Mekkorára válasszuk a G gömb sugarát ahhoz, hogy a felszinének a S gömb belsejébe eső része 1/5-öd része S felszínének?

"Megoldás:"

A G gömb felületéből az S gömb egy gömbsüveget metsz ki.
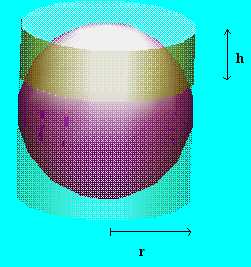A gömbsüveg felszínének a meghatározásához tudnunk kell, hogy az megegyezik a vele azonos magasságú, r alapkör-sugarú henger palástjának a felszínével, azaz .

Először h -t, majd az S belsejébe eső gömbsüveg felszínét adjuk meg r függvényeként. 


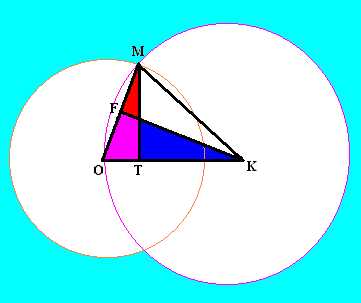
Legyen OM = 1 , OF =1/2 ,  OK=MK = r .  Ha a gömbsüveg h = OT magasságát keressük, kihasználhatjuk, hogy az OTM és az OFK hasonló háromszögek.
 
 

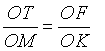Ebből:  , azaz  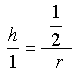, tehát a gömbsüveg magassága:  .

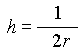Eszerint a kapott gömbsüveg felszíne 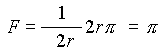 ,  vagyis a G gömbnek az S gömb belsejébe eső része a G sugarának megválasztásától függetlenül mindíg ugyanannyi, mégpedig az S gömb felszínének az 1/4 -ed része, így - mivel az 1/5-öd részt nem tudjuk előállítani - nem tudjuk a G gömb sugarát a feltételnek megfelelően megválasztani.

Helyesnek véli a megoldást?    Igen - Nem