Ezekkel a "megoldásokkal" találkozva mindenki nagy intenzitással kereste a hibát, hiszen mivel az állítás nyilvánvalóan hamis volt, vagy egy feladat eredménye nyilvánvalóan rossz, valahol kellett lennie egy (vagy több) hibának a bizonyításban, a feladat megoldásában.
I. F. Sharigin cikkét ( So, what's wrong? , QUANTUM , Vol 8, Number 6, July/August 1998., p. 34-37,53-54.) olvasva azonban találkoztunk néhány olyan feladattal, amelyben a kapott eredmény hihetőnek tűnt, a feladat megoldása korrektnek látszott. Ezért vált az eddigieknél is izgalmasabb kérdéssé, hogy: " Hol lehet a hiba? "
Ez a cikk adta az ötletet, hogy állítsunk össze egy feladatsorozatot, hozzá megadva egy megoldást is, amely azonban lehet, hogy rossz. Ugyanis az említett cikk feladatait kiegészítettük néhány további feladattal és megoldással. Annyival nehezítve a dolgot, hogy tettünk a feladatok közé valóban korrekt megoldásokat.
Így itt most találhat az olvasó igaz, vagy hamis állításokat tartalmazó feladatokat, a feladatokra adott megoldások ugyancsak lehetnek korrektek, lénygében jók, de hiányosak, vagy teljesen rosszak is.
Ezen a VEB
lapon csak a feladatokat adjuk meg. A ? jelre
kattintva talál az olvasó egy "megoldást", amelyet lehet elhinni, és lehet
kételkedni benne. Mielött azonban úgy döntünk, hogy "szabad a gazda", érdemes
kissé elgondolkoznunk, hátha a mi önállóan készített megoldásunk máris
kizárja a félrevezetés lehetőségét.
Aki mégis
megnézi a megoldást, onnan - néha - tobábbmehet olyan helyre, ahol a kételyeit
megerősíti, vagy éppen gyengíti az ott kapott információ. Bár az is lehet
hamis.
Mindehhez jó munkát kíván a feladatsorozat összeállítója:
1. feladat:
Egy négyszögalapú gúla alaplapjának két oldala 10, a másik kettő 6 egység. A gúla magassága 7. Mindegyik oldallap síkja 60 fokos szöget zár be az alaplap síkjával. Mennyi a gúla térfogata?
2. feladat:
Egy egységnyi sugarú S gömb középpontja illeszkedik egy másik, G gömb felületére. Mekkorára válasszuk a G gömb sugarát ahhoz, hogy a felszinének a S gömb belsejébe eső része 1/5-öd része S felszínének?
3. feladat:
Hány (valós)
megoldása van az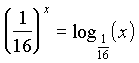 
egyenletnek?
4. feladat:
Megrajzolták egy egyenes körkúp csúcsán átmenő legnagyobb területű kúpmetszetet. Kiderült, hogy ennek a területe kétszerese a tengelymetszet területének. Mekkora a kúp félnyílásszöge (az alkotóknak a tengellyel bezárt szöge)?
5. feladat:
Keressük meg
azokat a p és
q számokat, melyek
kielégítik a 
egyenletet!
6. feladat:
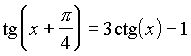trigonometrikus egyenletet!7. feladat:
Az ABCD paralelogramma, AB oldalának és BD átlójának a szöge 40 fok. Az ABC és CDA háromszögek köré írt körének középpontjai a BD átlóra illeszkednek. Milyen paralelogramma az ABCD ?
8. feladat:
Igazoljuk, hogy egyetlen olyan poliéder létezik, amelynek nincs átlója, (azaz bármely két csúcsát él köti össze) és ez a tetraéder.
9. feladat:
Vegyünk fel a síkon tetszőleges számú egyenest. Igazoljuk, hogy az egyenesekkel feldarabolt síkrészek kiszínezhetők mindössze két színnel úgy, hogy a szomszédos - közös szakasszal, vagy félegyenessel rendelkező - síkrészek különböző színűek legyenek.
10. feladat:
Adott a síkon n > 3 - különböző - pont, melyekről tudjuk, hogy bármely kettőhöz található egy olyan harmadik, amely illeszkedik a két pont által meghatározott egyenesre.
Igazoljuk, hogy az összes pont egy egyenesre illeszkedik.