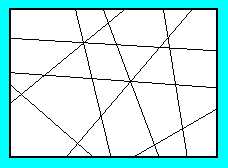
Vegyünk fel a síkon tetszőleges számú egyenest. Igazoljuk, hogy az egyenesekkel feldarabolt síkrészek kiszínezhetők mindössze két színnel úgy, hogy a szomszédos - közös szakasszal, vagy félegyenessel rendelkező - síkrészek különböző színűek legyenek.

"Megoldás:"

Az igazolást az egyenesek száma szerinti teljes indukcióval végezzük.

Ha csak egy egyenesünk van, akkor az általa meghatározott két félsík egyikét az egyik, másikát a másík színnel szinezzük ki.

Néhány további egyenest felvéve meggyőződhetünk arról, hogy ugyancsak el tudjuk végezni a helyes szinezést, bár ez nem része a bizonyításnak.

Tegyük most fel, hogy minden   k < n esetre megoldható a helyes szinezés.

Azt kell igazolnunk, hogy n egyenes esetén is megoldható. (n itt bármely pozitív egész szám lehet.)

A bizonyáshoz válasszunk ki az n egyenes közül egyet tetszés szerint. Ideiglenesen töröljük le.

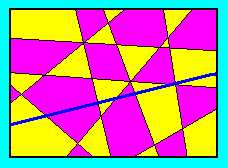
A megmaradt n -1 egyenesre alkalmazható az indukciós feltétel, azaz az általuk feldarabolt síkrészek kiszínezhetők helyesen két színnel. Ha most visszatesszük az ideiglenesen eltávolított egyenest, azt tapasztaljuk, hogy azoknál a tartományoknál hibás a szinezés, amelyek éppen e mentén szomszédosak.
 
 

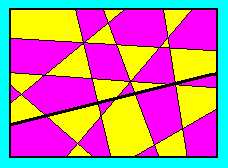Ha nost ennek az egyenesnek az egyik félsíkjában minden tartomány színét az ellenkezőjére változtatjuk, akkor a szinezés helyessé válik az n-edik egyenes mentén is, miközben mindenütt helyes marad, ahol eddig is helyes volt.

Tehát tetszőleges n egyenes esetén is kiszinezhetők két színnel a keletkezett síkrészek.

Helyesnek véli a megoldást?    Igen - Nem