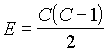 , mivel minden él két csúcshoz tartozik. A poliéder lapjai csak háromszögek
lehetnek, hiszen pl. egy négyszögnek már van átlója. Így - mivel minden
csúcsba C-1 háromszög
fut be - a lapok száma
, mivel minden él két csúcshoz tartozik. A poliéder lapjai csak háromszögek
lehetnek, hiszen pl. egy négyszögnek már van átlója. Így - mivel minden
csúcsba C-1 háromszög
fut be - a lapok száma 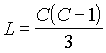 ugyancsak azért, mert egy lap három csúcshoz tartozik.
ugyancsak azért, mert egy lap három csúcshoz tartozik.
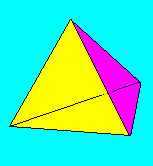
Igazoljuk, hogy egyetlen olyan poliéder létezik, amelynek nincs átlója, (azaz bármely két csúcsát él köti össze) és ez a tetraéder.
"Megoldás:"
Legyen a feltételeknek
elegettevő poliédernek C
csúcsa. Mivel bármely két csúcsnak van közös éle, ezért egy csúcsból C-1
él induk ki, így az élek száma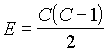 , mivel minden él két csúcshoz tartozik. A poliéder lapjai csak háromszögek
lehetnek, hiszen pl. egy négyszögnek már van átlója. Így - mivel minden
csúcsba C-1 háromszög
fut be - a lapok száma
, mivel minden él két csúcshoz tartozik. A poliéder lapjai csak háromszögek
lehetnek, hiszen pl. egy négyszögnek már van átlója. Így - mivel minden
csúcsba C-1 háromszög
fut be - a lapok száma 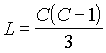 ugyancsak azért, mert egy lap három csúcshoz tartozik.
ugyancsak azért, mert egy lap három csúcshoz tartozik.
Végül - mivel
egy átló nélküli poliédernek szükségképpen konvexnek kell lennie, és minden
konvex poliéder egyszerű - alkalmazható a keresett poliéderre Euler poliéder-tétele,
miszerint az egyszerű poliéderek lapjainak, csúcsainak és éleinek a száma
között fennáll az L + C - E = 2
összefüggés: 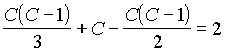 .
.
Így C-re egy másodfokú egyenletet kaptunk, melynek a gyökei C = 3 és C = 4 . Ezek közül - mivel egy poliédernek legalább 4 csúcsa van - csak az utóbbi jelent megoldást, ez pedig valóban a tetraéder.
Helyesnek véli a megoldást? Igen - Nem