SIERPINSKI
SZIVACS-különbözõ dimenziókban
1.
Sierpinski háromszög
A Sierpinski Szivacs
egy olyan közismert fraktál,amit aránylag könnyû
elkészíteni. Ennek a fraktálnak a háromszög
verzióját többféle módon is elõállíthatjuk.
Erre a legegyszerûbb módszer, ha rajzolunk egy egyenlõ
oldalú háromszöget, és ezt további négy
egyenlõ oldalú háromszögre bontjuk, melyek közül
az egyik háromszög lefelé fog mutatni. Ezt a lefelé
mutató háromszöget távolítjuk el. A megmaradt
háromszögeket ismét négy egyenlõ oldalú
háromszögre osztjuk, a lefelé mutató háromszögeket
pedig megint eltávolítjuk.

Ezt a mûveletet
újra és újra elvégezve a kis háromszögek
egyre kevésbé fognak látszani.

Egy másik módszer a "Káosz
Játék". Adott három pont-az egyenlõ szárú
háromszög csúcsai-a síkon. A háromszög
tetszõleges pontjával kezdjük, és egy tetszõlegesen
kiválasztott csúcs és a pont közötti szakasz
felezõpontját berajzoljuk. Ezt a mûveletet többször
is megismételjük, míg végül a pontok egy
Sierpinski háromszöget határoznak meg.
Mi a kapcsolat a Pascal
háromszög és a Sierpinski háromszög
között?
Hány
dimenziós a Sierpinski háromszög?
2.
Sierpinski tetraéder
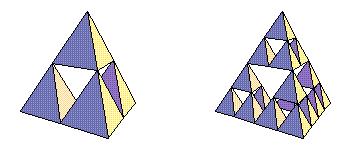
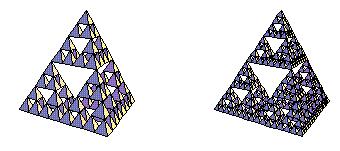
Amint az ábrán láthatjuk, a Sierpinski tetraéder
lapjai Sierpinski háromszögek.
Érdekességkét
megjegyezzük, hogy azok a poliéderek amelyeket eltávolítunk
a Sierpinski tetraéderbõl nem tetraéderek, mint ahogy
gondolnánk, hanem oktaéderek. A Sierpinski tetraédert
a háromszöghöz hasonló módon állíthatjuk
elõ. Elsõ lépésben a teraéder
közepébõl eltávolítjuk az oktaédert,
így négy kis szabályos teraédert kapunk. Ezután
a kisebb tetraéderek közepébõl is eltávolítunk
egy-egy oktaédert, és így tovább. A "Káosz
Játék" segítségével ugyancsak elõállítható
a Sierpinski tetraéder.Vajon a Pascal
háromszög segítségével
is? Mindezek után felmerülhet még egy kérdés:
Hány
dimenziós a Sierpinski tetraéder?
És végül azoknak ajánlanék
a témához kapcsolódó oldalakat az interneten,
akik tudnak angolul:
http://www.shodor.org/interactivate/activities/gasket/
http://serendip.brynmawr.edu/playground/sierpinski.html
http://www.palmyra.demon.co.uk/illusion/geometry/siertetr.gif
http://www.math.sunysb.edu/~scott/mat331.spr98/samples/fractals/sierp3d/sierp3d.html
