
A szabályos poliédereknek, pl. az ikozaédernek, vagy a dodekaédernek, esetleg e két alakzat metszete-ként elõálló alakzatnak az un. ikozidodekaédernek a felhasználásával számos igen tetszetõs, érdekes szimmetriát mutató geometriai alakzat készítésére nyílik lehetõség.

Munkánk igényel némi - matematikai - elemzést, amit viszont nem nagyon mellõzhetünk, ha nem csak a "Mit kaptunk?", hanem a "Hogyan kaptuk?" kérdést is szem elõtt szeretnénk tartani.
Induljunk ki
a dodekaéder egy élvázas modelljébõl.
Mivel a dodekaéder csúcsai közül alkalmasan kiválasztható
nyolc olyan, melyek egyben egy kocka csúcsai is, a kocka csúcsai
közül pedig alkalmasan kiválasztható három
olyan, melyek egyben egy szabályos háromszög csúcsai,
a dodekaéderen is találunk három, szabályos
háromszöget alkotó csúcsot. Ilyen például
az ![]() : p1.wrl
.
: p1.wrl
.
Az alábbi VRML fájlok szerkesztéséhez jórészt az e sorok írója által fejlesztett VRML szerkesztõ programot fogjuk alkalmazni, így arról, aki nyomon szeretné követni az itt bemutatott "mûhelymunkát", feltételezzük, hogy ismeri, és kellõ biztonsággal használja ezt a programot.
Lehet, hogy
feltûnt figyelmesebb olvasóinknak, hogy ebben a VRML fájlban
betûket lát számok helyett, ezt viszont a mi szerkesztõnk
nem tudja elõállítani. Ugyanígy, kissé
áttetszõ az ![]() lap. Megtehetjük, hogy egy VRML fájlba "kézzel" belenyúljunk,
hiszen ez nem csak a VRML megjelenítõ, hanem a mi számunkra
is ( remélhetõleg) érthetõ ASCII kódú
program, amely bármely vezérlõjeleket nem tartalmazó
szövegszerkesztõvel szerkeszthetõ. Praktikus pl. erre
a célra a PASCAL szerkesztõt használni, ezzel ugyanis
könnyen átvihetünk program-részleteket egyik fájlból
a másikba.
lap. Megtehetjük, hogy egy VRML fájlba "kézzel" belenyúljunk,
hiszen ez nem csak a VRML megjelenítõ, hanem a mi számunkra
is ( remélhetõleg) érthetõ ASCII kódú
program, amely bármely vezérlõjeleket nem tartalmazó
szövegszerkesztõvel szerkeszthetõ. Praktikus pl. erre
a célra a PASCAL szerkesztõt használni, ezzel ugyanis
könnyen átvihetünk program-részleteket egyik fájlból
a másikba.
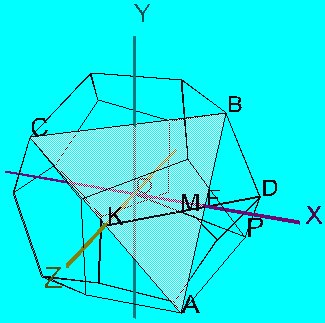
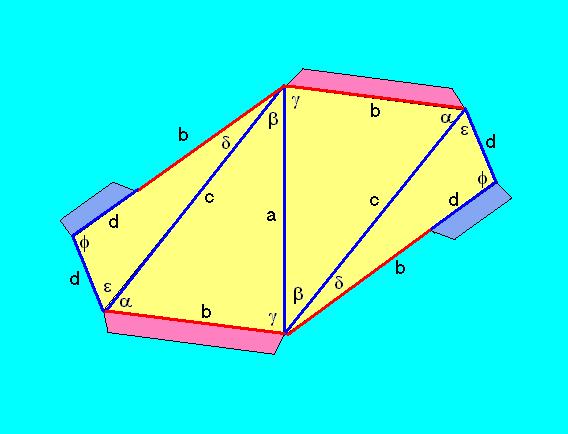
Nos, az ![]() -nek
( a csúcsok koordinátái:
-nek
( a csúcsok koordinátái:![]()
![]()
![]() ) a síkja tartalmaz a dodekaéder csúcsai közül
még hármat, pl. a
) a síkja tartalmaz a dodekaéder csúcsai közül
még hármat, pl. a ![]() pontot, amelyrõl könnyen be lehet látni, hogy illeszkedik
az
pontot, amelyrõl könnyen be lehet látni, hogy illeszkedik
az ![]()
![]() középvonalának az egyenesére, a
középvonalának az egyenesére, a ![]() ,
, ![]() pontokon
átmenõ egyenesre. Az is nyilvánvaló, hogy ez
az egyenes metszi ( az
pontokon
átmenõ egyenesre. Az is nyilvánvaló, hogy ez
az egyenes metszi ( az ![]() pontban) az origón , valamint a
pontban) az origón , valamint a ![]() pontokon átmenõ
pontokon átmenõ ![]() egyenest, hiszen mindkettõ az XZ síkban
van. Még - némi számolással - azt is meg tudjuk
határozni, hogy ennek a metszéspontnak a koordinátái
egyenest, hiszen mindkettõ az XZ síkban
van. Még - némi számolással - azt is meg tudjuk
határozni, hogy ennek a metszéspontnak a koordinátái![]() arányú
zsugorítással állnak elõ a
arányú
zsugorítással állnak elõ a![]() pont koordinátáiból. (
pont koordinátáiból. (![]() továbbra is az aranymetszés arányát jelöli:
továbbra is az aranymetszés arányát jelöli:![]() .)
.)
Egy olyan csillag-poliédert
fogunk építeni, amelynek a lapjai matematikai szempontból
nézve egybevágó önátmetszõ négyszögek.
A fenti vizsgálatokat azért végeztük, hogy egy
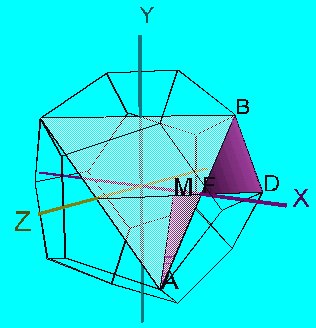
ilyen négyszöget elõállítsunk, ez az![]() négyszög. Technikai szempontból
ez természetesen két háromszögre az
négyszög. Technikai szempontból
ez természetesen két háromszögre az ![]() és az
és az ![]() háromszögre bomlik. Ebben a sorrendben
felsorolva a két háromszög csúcsait, és
bekapcsolva A VRML szerkesztõnknek azt a funkcióját,
hogy csak a pozitív körüljárású síklapokat
lássuk, kicsit talán érzékeltetni tudjuk, hogy
a négyszögünk önátmetszõ. p2.wrl
.
háromszögre bomlik. Ebben a sorrendben
felsorolva a két háromszög csúcsait, és
bekapcsolva A VRML szerkesztõnknek azt a funkcióját,
hogy csak a pozitív körüljárású síklapokat
lássuk, kicsit talán érzékeltetni tudjuk, hogy
a négyszögünk önátmetszõ. p2.wrl
.
Innen kezdve
a feladatunk elvileg egyszerû, gyakorlatilag technikai jellegû,
és kissé hosszadalmas. Ezt a körüljárási
irányt megtartva a dodekaéder minden élére
illesszünk rá egy az![]() négyszöggel egybevágó
négyszöget, ezzel megkapjuk a keresett csillag-poliédert.
Azt, hogy ezzel valóban (közönséges, bár
önátmetszõ lapokkal rendelkezõ) poliédert
kapunk, még be kellene látnunk. Lényegében
azt kellene igazolnunk, hogy az
négyszöggel egybevágó
négyszöget, ezzel megkapjuk a keresett csillag-poliédert.
Azt, hogy ezzel valóban (közönséges, bár
önátmetszõ lapokkal rendelkezõ) poliédert
kapunk, még be kellene látnunk. Lényegében
azt kellene igazolnunk, hogy az ![]() alakzat
minden élére pontosan még egy ugyanilyen alakzat azonos
hosszúságú éle illeszkedik. (Ismételten
hangsúlyozzuk a körüljárási irányt.)
alakzat
minden élére pontosan még egy ugyanilyen alakzat azonos
hosszúságú éle illeszkedik. (Ismételten
hangsúlyozzuk a körüljárási irányt.)
Most mellõzzük
még ezt a feladatot, helyette irányítástartó
egybevágósági transzformációkkal és
az így kapott fájlok összefésülésével
lássunk neki az alakzat elõállításának.
Azt azért nem árt elõre tudnunk, hogy minden egyes
dodekaéder-élhez két ilyen négyszögnek
kell tartoznia, vagyis az alakzatunk összesen 30*2
négyszögbõl, gyakorlatilag 120
db. háromszögbõl fog állni. Csúcsai -
ugyancsak elvileg - az eredeti dodekaéderünk csúcsi,
valamint az ebbõl ![]() arányú
zsugorítással kapott (Az
arányú
zsugorítással kapott (Az ![]() pont transzformálásával elõálló)
dodekaéder csúcsi lesznek melyekhez
- gyakorlatilag - hozzáadódnak még az
pont transzformálásával elõálló)
dodekaéder csúcsi lesznek melyekhez
- gyakorlatilag - hozzáadódnak még az ![]() pont transzformálásával kapott pontok, melyek éppen
egy ikozidodekaéder csúcsait alkotják.
Ez utóbbiak azonban nem csúcsai az alakzatnak, hanem a négyszögek
önátmetszõ pontjai. (A figyelmesebb olvasó már
bizonyára észrevette, hogy a korábban elõállított
ikozidodekaédert nem véletlenül mutattuk be a
WEB-lapunk elején. Egy-egy ilyen alakzatot nem csak amiatt érdemes
elkészíteni, mert érdekes, netán szép,
hanem azért is, mert "hátha jó lesz még valamire".
Ez máris bekövetkezett.)
pont transzformálásával kapott pontok, melyek éppen
egy ikozidodekaéder csúcsait alkotják.
Ez utóbbiak azonban nem csúcsai az alakzatnak, hanem a négyszögek
önátmetszõ pontjai. (A figyelmesebb olvasó már
bizonyára észrevette, hogy a korábban elõállított
ikozidodekaédert nem véletlenül mutattuk be a
WEB-lapunk elején. Egy-egy ilyen alakzatot nem csak amiatt érdemes
elkészíteni, mert érdekes, netán szép,
hanem azért is, mert "hátha jó lesz még valamire".
Ez máris bekövetkezett.)
Mint már
láttuk, szerkesztõnk segítségével könnyen
elõállíthatjuk azokat az egybevágósági
transzformációkat, amelyek valamely kiválasztott pontot
valamelyik kiválasztott koordináta-tengelyre illesztik. Ehhez
célszerû készítenünk egy "sablont", amelyrõl
leolvasható, hogy milyen pontokat kell kiválasztanunk ahhoz,
hogy alakzatunkat meghatározott helyzetbe transzformáljuk,
például, hogy az ![]() négyszög síkját
valamely tengelyre merõleges helyzetbe hozzuk.
négyszög síkját
valamely tengelyre merõleges helyzetbe hozzuk.
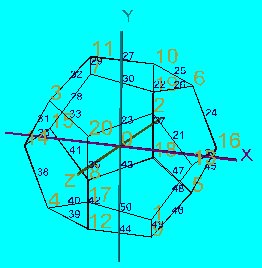
Ez a sablon.wrl fájl úgy készült, hogy elõbb a dodekaéder, majd az ikozidodekaéder adatait olvastuk be a szerkesztõnkbe. Az összefésült fájlnak elõször kitöröltük az összes lapját, majd az ikozidodekaéderhez tartozó éleket is, minden csúcs sorszámát kiírattunk, végül ebbe a fájlba is belenyúltunk kicsit "kézzel": Más színt és betûméretet használva különböztetjük meg a dodekaéder csúcsainak, ill. élfelezõ-pontjainak a koordinátáit.
Ha ebbõl az alakzatból fogjuk leolvasni a szükséges transzformációkat, akkor elsõként ezt a fájlt, ezt követõen a transzformálásra kiszemelt ( pl. a p2.wrl) fájlt olvassuk be, ezzel elérjük, hogy a transzformációkhoz használt pontok sorszáma - a dodekaéder csúcsait és él-felezõ pontjait illetõen - ugyanaz legyen, mint a sablonfájlban: p3.wrl.
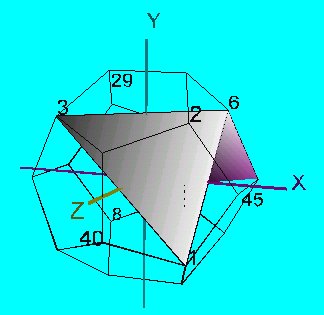
Egyelõre
segíti a tájékozódást az ![]() háromszög, amelyet mindkét
körüljárással felvettünk, így mindkét
oldala felõl nézve látszik, miközben a poliédeünket
alkotó háromszögek csak a leendõ külsõ
oldaluk irányából látszanak.
háromszög, amelyet mindkét
körüljárással felvettünk, így mindkét
oldala felõl nézve látszik, miközben a poliédeünket
alkotó háromszögek csak a leendõ külsõ
oldaluk irányából látszanak.
. Ha azt szeretnénk, hogy ez a sík pl. az Y tengelyre legyen merõleges, akkor a 2. pontot kell az Y tengelyre, és a (0,2) egyenes normálsíkjának egy pontját, pl. a 45. -t az X (vagy a Z ) tengelyre illesztenünk. Jelöljük ezt így, a kiválasztás sorrendjében: Y:=(2) X :=(45) . Az origó természetesen helyben marad: p3a.wrl . Akár ezt, akár a p3.wrl -t tovább transzformálva rendre elõ tudjuk állítani ennek az alakzatnak a (2,8) tengely körüli 120 fokos elforgatottjait. Az Y:=(2) X :=(29) transzformáció eredménye p3b.wrl ,az Y:=(2) X :=(40) transzformációé pedig p3c.wrl . (Elegendõ volt a szerkesztõbe egyszer beolvasott p3.wrl fájlt rendre tovább transzformálni.)
Az így kapott fájlokat összefésülve megkapjuk a három, egy síkban fekvõ önátmetszõ négyszöget: p3abc.wrl . Ha az összefésüléskor összevontuk az egybeesõ csúcsokat, de a lapokat nem, akkor az (1,3,6) háromszögünk már 6 példányban szerepel a fájlban.
Egy újabb
egybevágósági transzformációval: Y:=(8)
X :=(45) - amely lényegében
egy X tengely körüli 180 fokos forgatás - elõ tudjuk
állítani az ezzel párhuzamos síkban fekvõket
is, melyeket az eredetivel összefésülve megkapjuk az összes
olyan "négyszöget" (technikailag 12 db. háromszöget),
melyek síkja(i) merõlegesek a dodekaéder két
szemközti csúcsát összekötõ egyenesére:
p4.wrl .
Ebbõl most már töröljük ki a csúcsok sorszámait, az összes élt, az eddig a támpontul szolgáló szabályos háromszögeket, végül minden felesleges csúcsot is. Adjunk a lapoknak egy késõbb átírandó - pl. fehér - színt: alap.wrl .
Mivel alakzatunk 120 darab háromszögbõl fog állni, valami szisztémát célszerû kidolgoznunk a lapok színeinek a megválasztására. Egyelõre állapodjunk meg abban, hogy az alakzat egymással párhuzamos - ill. egybeesõ - síkban fekvõ lapok kapják ugyanazt a színt. Mivel egy dodekaédernek 20 csúcsa, így 10 szemben fekvõ csúcs-párja van, ez tíz színt fog jelenteni.
Eljárásunknak a lényege, hogy megfelelõ transzformációkkal olyan irányba állítjuk a sablonfájlunk dodekaéderét, hogy az alap-alakzatunkat hozzáolvasva újabb és újabb más-más színû lapokkal bõvüljön az alakzatunk.
Ezt kissé részletezve az eljárás sorozatunk az alábbi lépésekbõl fog állni.
y02x45.wrl y10x37.wrl y11x41.wrl y03x39.wrl 20x49.wrl
y13x26.wrl y06x28.wrl y07x22.wrl y14x27.wrl y17x32.wrl
A kész alakzat eredeti helyzetében:

Ugyanezt az arany-dodekaédert más - ugyancsak következetes - szisztéma szerint is kiszínezhetjük. Például úgy, hogy azt a négy lapot (a két nagyobb és két kisebb háromszöget), amelyek "körülvesznek" egy dodekaéder-élt ugyanolyan színûre festünk. Emellett még arra is ügyelhetünk, hogy - éppúgy, mint eddig - az egy doekaéder-lap éleire illeszkedõ lapok mind különbözõ színt kapjanak.
Ezt a színezést az is indokolja, hogy amennyiben (pl. papírból) el szeretnénk készíteni az alakzat modelljét, ezt a négy lapot célszerû együtt kivágnunk.
Nehezebb feladat
lenne a 120 háromszögbõl álló alakzatunkat
ennek megfelelõen átszínezni, mint újból
elõállítani.
Ezért
egy adott dodekaéder él körüli négy
háromszöglap kivételével töröljük
le az alakzat összes lapját. Ebbõl az alakzatból
( 4lap1.wrl ) fogjuk felépíteni
újból az arany-dodekaédert, a fenti elveknek megfelelõ
módon.
Az egész poliéder újraépítéséhez célszerû egy új "sablont" készítenünk, amely az ikozidodekaéder csúcsai mellett az ikozaéder csúcsait tartalmazza. Ezt használhatjuk ugyanis arra a célra, hogy az alakzatunkat úgy helyezzük el egy koordináta-rendszerben, hogy a konvex burkát alkotó dodekaéder két lapja legyen párhuzamos a (vízszintesnek tekinthetõ) XZ síkkal.
Az új alapalakzatunk most 5*4 azonos színû háromszögbõl fog állni. Ezt az elõbb megismert, itt már nem részletezett módon az új sablonfájlunk és az 4lap1.wrl összefésülésével és transzformálásával állítjuk elõ elõször az y12x48.wrl fájlt, a 12. számú pontot az Y a 45. -et az X tengelyre állítva. Ennek a fájlnak készítsük el azt a változatát is, amely pusztán a lapokat tartalmazza: 4lap2.wrl . Ugyanis ezt fogjuk majd rendre összefésülni az y12x48.wrl fájl tovább transzformált változataival. (Erre a célra használhatnánk magát az y12x48.wrl fájlt is, de a szerkesztõ programnak ekkor sokat kellene bíbelõdnie az egybeesõ csúcsok összevonásával.)
Nos, a forgatások és
összefésülések eredményeként állnak
elõ rendre az y12x55.wrl
y12x57.wrl y12x33.wrl
y12x45.wrl
fájlok, melyek közül az utolsót - az elõbbivel
megegyezõ okból - ugyancsak megszabadítjuk a felesleges
csúcsoktól és élektõl: alap2.wrl
. Ezek a forgatások lényegében az Y
tengely körüli ![]() nagyságú forgatások voltak.
nagyságú forgatások voltak.
A már megismert módon tovább transzformáljuk az y12x45.wrl fájlt, megváltoztatjuk az utolsóként hozzáolvasott lapok színét, majd összefésüljük az alap2.wrl fájllal. Így kapjuk rendre az y2x43.wrl y3x53.wrl y6x42.wrl y9x40.wrl y5x54.wrl fájlokat, melyek közül az utolsó már a végsõ arany2.wrl fájl.


Munkánk közben célszerû elmentenünk a VRML szerkesztõnk által kiszámolt transzformációs mátrixok fájljait (ty2x43.wrl ty3x53.wrl ty6x42.wrl ty9x40.wrl ty5x54.wrl), ugyanis ezekbõl a VRML fájl közvetlen szerkesztésével igen egyszerûen elõállítható az alakzat. Fontos megjegyezni, hogy ezek a mátrixok rendre az Y tengelyre merõleges helyzetbe állítják a dodekaéder lapjait. Mivel az új helyzet mindig az elõzõbõl áll elõ, az itt kialakított sorrend nem változtatható meg.
Vegyük most "kézbe" a VRML fájl szerkesztését valamely ASCII kódú szövegszerkesztõt használva. A 4lap.wrl alakzatból könnyedén elõ tudjuk állítani az azonos színû lapokat egy Y tengelyû, 2*Pi/5 nagyságú forgatással, melyet négyszer kell alkalmaznunk: alap3.wrl Ebbõl pedig az imént kiszámított mátrix transzformációkkal újból megkaphatjuk az arany-dodekaédert: arany3.wrl . Ehhez fordított sorrendben kell alkalmaznunk a transzformációkat, hiszen most nem az egész alakzatot forgatjuk olyan helyzetbe, hogy összefésülhessük az alapalakzattal, hanem az alapalakzatot fordítjuk más és más helyzetbe. Ezzel egy kissé rövidebb forrásfájlt kapunk, hiszen nem kell minden pont koordinátáját külön-külön megadnunk: arany3.txt .
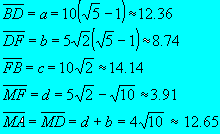
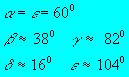
Az alakzat rajzán kék
színnel jelöltük az élt, ha a hozzá tartozó
lapszög konvex, pirossal, ha konkáv. Az egymáshoz illesztendõ
élek közül csak az egyikhez illesztettünk "fület",
ahhoz, amelyik a modellkészítés szempontjából
jobban kézre esik. A papír-modell elkészítéséhez
ebbõl a "sablon"-ból, összesen 30 darabra van
szükség, az itt látott színezési szisztémához
6 színbõl kell 5-5 ilyen alakzatot készítenünk.
Vegyük még egyszer szemügyre
az arany-dodekaédert! Ha csak egy színre
figyelünk, támadhat olyan érzésünk, mint
ha az ebbõl a színbõl álló alakzat egyszer
felülrõl, egyszer alulról "kerüli
meg" a dodekaéder éleit. Tegyük kissé
képlékenyebbé ezt a jelenséget. Ehhez
készítsünk két tóruszt,
melyek közül az egyik - pontosan ötször - körbe
tekeredik a másik körül.
Ezeket a tóruszokat a MAPLE
release 5 verziójával szerkesztettük, amely az
általa elõállított térbeli alakzatokról
VRML fájlokat is tud készíteni: Ez a program
forrásfájlja: spiral.mws , a forrás
szövege: spiral.txt és az általa
elõállított vrml fájl: spiral.wrl.
Ha most ezt a fájlt beillesztjük
az arany3.wrl fájlba az azonos színû lapokat elõállító
rész helyére, egy pillanat alatt hozzájutunk
egy igen látványos VRML jelenethez.

Ha pedig csak a tórusszal végezzük el ezeket a transzformációkat, kissé más formában ugyan , de visszajutunk a kiindulásul vett ikozidodekaéderhez.
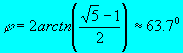 .
.

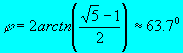 nagyságú szöggel elforgatva egy újabb tóruszt
kapunk, amelybõl pedig egy az eredeti tóruszunk síkjára
merõleges tengely körül
nagyságú szöggel elforgatva egy újabb tóruszt
kapunk, amelybõl pedig egy az eredeti tóruszunk síkjára
merõleges tengely körül Mindezt az öt csavarással elõálló spiráunkkal is megtehetjük, csak a legelsõt a lerajzolás elõtt alá kell vetnünk egy a síkjára merõleges 180 fokos forgatásnak. Mindez könnyen és röviden megvalósítható a MAPLE segítségével, amely az egész VRML fájl elõállítását is elvégzi helyettünk. Az alábbi VRML fájlok ezzel a spiralok.mws MAPLE programmal készültek, melynek ez a forrásfájlja: spiralok.txt.
A spirál formáját lényegében két bemenõ adat határozza meg:
(A keletkezõ VRML jelenet minõségét, az interaktív mozgatás sebességét - méginkább a fájl méretét - befolyásolja az is, hogy a tóruszok megadásához milyen "finom" beosztást alkalmazunk, így ez a két adat - numpoints = a , tubepoints = b - ugyancsak bemenõ paraméterként szerepel a spirál elõállításánál.)
d = 0.5; ro = 0.4 : "szelídebb" kanyarokat leírva áttekinthetõbb a kép: 6sp2.wrl ;
d = 3; ro = 0.75 : ha meggyõzõdtünk róla, hogy két spirál nem metszi egymást, akkor a konstrukció szimmetriáiból adódóan semelyik kettõnek sincs közös pontja: 2sp3.wrl ; 6sp3.wrl ;
d=7; ro = 0.3 : ugyanez akkor is igaz, ha spirálok szinte áttekinthetetlenül kusza alakzatban kerülgetik ki egymást: 2sp4.wrl ; 6sp4.wrl ;
A MAPLE felhasználók számára ajánljuk, hogy keressenek további nem metszõ eseteket.
Ezeket a forgatásokat az alap3.wrl alapalakzatunkra alkalmazva ezzel az igazán nem nagy fájllal - arany4.txt - is elõállíthatjuk az arany dodekaédert: arany4.wrl .
A "saját mûhelyükben" végzett munkájukhoz sok sikert, az önálló felfedezés örömét kívánja: