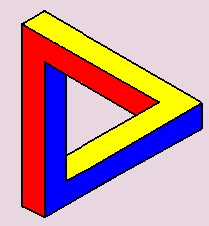
Escher sok munkájának alapja ez a "lehetetlen háromszög", amely három négyzet keresztmetszetű gerendából áll, melyek derékszögben kapcsolódnak egymáshoz.

Maga a művész így jellemezi az alakzatot:

"Ha ennek a konstrukciónak minden részét nyomon követjük a szemünkkel, egyetlen hibára sem lelünk. Mégis lehetetlen az egész, mert a szemünk és a tárgy közötti távolság interpretációja során változások lépnek fel. "

Az ötletet kihasználva konstruálta Escher ezt a kissé bonyolultabb rajzot. amely ugyancsak lehetetlen (vagyis a valóságban nem létező) alakzat:

Valóban lehetetlen?    Nézőpont kérdése (a szó szoros értelmében).

Elegendő, ha a megfelelő térbeli alakzatról egy olyan ortogonális axonometikus képet készítünk, amelyben a térbeli koordinátarendszer mindhárom tengelye ugyanakkora szöget zár be az axonometrikus képsíkkal, így a képen a tengelyek 120 fokos szöget zárnak be egymással. (A vetítősugarak természetesen merőlegesek az axonometrikus képsíkra.)

Ha egy kockáról készítünk ilyen, un. izometrikus (egyméretű) axonometrikus képet, akkor annak a nem látható, és a hozzánk legközelebbi csúcsa a képen egybeesik.

Igy az alakzatunkat néhány alkalmas kockával kiegészítve világos lesz, hogy mi okozza az ellentmondást:

Ez az alakzat is többeknek adott ötletet. Itt van például ez a kedves kis fejtörő: töltse le, bontsa ki, majd futtassa a programot a kedves olvasó. A feladat az, hogy állítsuk össze a jobboldali - lehetetlen - háromszöget.

Az izometrikus axonometia által okozott érzéki csalódást használta ki Escher a következő rajzában:

A lehetetlen háromszögről e műve kapcsán Escher a következőket írta:

"A képen ez a lehetetlen háromszög háromszor is szerepel. Lehulló víz mozgatja a malomkereket, és folyik tovább lefelé egy erősen lejtő csatornán, két torony közt, lassan, cikkcakkban egészen addig a pontig, ahol a vízesés ismét kezdődik. A molnárnak időnként egy vödör vizet kell hozzáöntenie, hogy a párolgás következtében keletkezett veszteséget pótolja. A két torony egyforma magas, mégis a jobb oldali egy emelettel alacsonyabb, mint a bal oldali."

Ez bizony igen szép példája annak a vizuális humornak, amely talán a legfőbb jellemzője Escher művészetének. Van egyfajta kellemes kajánság abban, ahogy Escher tréfát űz a térszemléletünkkel.

Ha már alaposan szemügyre vettük ezt a képet, javasolunk az érdeklődők számára egy szép, remélhetően nem túl nehéz feladatot: készítsünk VRML jeleneteket a tornyok tetején álló alakzatokról!

A baloldali torony tetején egy három kockából álló alakzatot látunk:

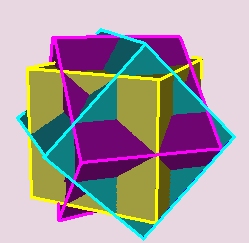
Ez a kép egy VRML fájl alapján készült. Lényegében egy dolgot kellett megoldanunk, azt, hogy milyen irányú tengely körül, mekkora szöggel kell elforgatnunk a kockát, hogy ezt az alakzatot kapjuk. Mivel senkit nem szeretnénk megfosztani az önálló alkotás örömétől, itt most közöljük a kép elkészítéséhez használt VRML forrásprogramot, csak éppen a lényeget, a forgatások adatait nem adjuk meg.

Érdekes, hogy a jobboldali toronyra illesztett alakzat előállításához pontosan ugyanazokat a forgásokat kell alkalmaznunk. Az ehhez szükséges VRML fájl elkészítését teljes egészében az olvasóra bízzuk. Itt az a fő kérdés, hogy milyen alakzatból (poliéderből) kapjuk a megfelelő forgatásokkal a keresett alakzatot.