Kérjük, töltse le, majd futtassa a vrmlsz.exe programot.
Ez egy - DOS alatt (is) futó - program amelynek az a feladata, hogy megkönnyítse síklapokból álló vrml fájlok készítését. A program szabadon terjeszthetõ, másolható, a kereskedelmi célú sokszorosítást kivéve.
Ezzel együtt a szerzõ - miután nem kevés munkája fekszik a program fejlesztésében - szívesen olvasna minden olyan elektronikus levelet, amelyben tudomást szerezne arról, hogy kik töltötték le a programot, mennyire voltak elégedettek a használatával, voltak-e technikai, vagy matematikai jellegû problémáik a program használata közben. Az esetleges kérdésekre is készséggel válaszolna. (E-mail: szilassi@jgytf.u-szeged.hu )
A program használata nem igényel számítástechnikai ismereteket, azonban ajánljuk a program HELP menüjének az alapos tanulmányozását.
Javasoljuk, hogy a programot párhuzamosan használja valamely vrml megjelenítõvel, amellyel a szerkesztés eredményét folyamatosan nyomon tudja követni. Eddigi tapasztalataink szerint legkényelmesebb a Netscape Navigator Gold browser Live3D programjának a használata.
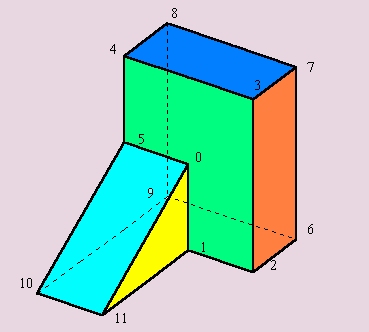
Egy a mintapéldán keresztül szeretnénk megismertetni az érdeklõdõkkel a program által nyújtott lehetõségeket. Tûzzük ki célul ennek a geometriai alakzatnak a megjelenítését:

Ahhoz, hogy szerkesztõnkkel elkezdhessük a munkát, célszerû papíron (vagy legalább fejben) megterveznünk, hogy miként vegyük fel az alakzatunk derékszögû koordinátáit. Ez fõként matematikai probléma, amely attól függõen könnyebb, vagy nehezebb, hogy mit szeretnénk ábrázolni. Ügyelnünk kell a pontok felvételének a sorrendjére, ugyanis késõbb, a lapok, ill. a pontokat összekötõ szakaszok megadásánál a pontokra sorszámaikkal kell hivatkoznunk. Bár - mint késõbb látni fogjuk - lesz lehetõségünk arra, hogy a megadott alakzatot elmozdítsuk a koordinátarendszerhez képest, azonban már most célszerû olyan koordinátákat felvennünk, hogy az origó lehetõleg az alakzat "közepe táján" legyen. Ugyanis így az origó körüli forgatás nem viszi ki az alakzatunkat a látóterünkbõl.
A programot elindítva nyilvánvalóan a "pontok megadása" az elsõ teendõnk. Ha már van legalább egy lapnyi csúcspontunk, ezt a lapot vegyük is fel, és jelenítsük meg az alakzatot, hogy legyen támpontunk a további munkához. A program megismerésének az a legjobb útja, ha megpróbálja a felhasználó az itt látottakhoz hasonló formában rendre elõállítani és megjeleníteni a most bemutatott vrml fájlokat.
Ha nem sikerült az elsõ síklap megadása, (mert pl. úgy adtuk meg a koordinátákat, hogy azok nincsenek egy síkban, vagy olyan sorrendben szerettük volna összekötni õket, hogy abban a sorrendben nem alkotnának egyszerû sokszöget, azaz metszenék egymást az élek, akkor jelenítsük meg a pontok sorszámait ("pontok sorszámozása" menüpont), majd a "megjelenítés" menüpontban állítsuk úgy a paramétereket, hogy lássuk a koordinátarendszert is. A "szakaszok megadása" menüpont ugyancsak a segítségünkre lehet. Itt az eredmény.
Ha rosszul látszanak a vonalak a képernyõnkön, változtassunk a háttér színén a "Háttérszín" menüponttal. A háttér színét épp úgy, mint az egyes lapok színeit - az un. RGB színeket - egy 0 és 1 közötti számokból álló számhármassal jellemezhetjük. Természetesen újból tárolnunk kell az aktuális beállítást, majd a használt megjelenítõn újra be kell olvasnunk a módosított fájlt. Pl. a Netsape Navigatort használva a "Reload" menüponttal érvényesíthetjük a változtatást a megjelenítésben is. ( Ebben a leírásban a továbbiakban a Live3D megjelenítõre többször fogunk hivatkozni, feltételezve, hogy a kedves olvasó ezt használja.)
Célszerû rendre felvennünk az alakzat összes pontját, megjelenítve a sorszámaikat, esetleg az õket összekötõ szakaszokat. Egy-egy rosszul felvett koordinátát megváltoztathatunk, ha ezzel nem lépünk ki annak a lapnak a síkjából, amely tartalmazza a módosítandó csúcsot. Ha a program nem engedi a változtatást, legjobb ideiglenesen kitörölnünk az akadályt okozó lapot. Az így kapott élvázas rajzon megszemlélhetjük, hogy milyen sorszámú pontokat milyen sorrendben kell megadnunk egy-egy lap definiálásához. Ha az ábránk az alaphelyzetnek megfelelõen perspektív, akkor a megjelenítõnk walk funkciójával tetszõlegesen közel mehetünk a bennünket érdeklõ részlethez.
Itt jegyezzük meg, hogy ugyanazokkal az adatokkal többféle megjelenítést is elérhetünk a "megjelenítés" címû programrészlettel, amely lényegében kilenc darab kétállapotú kapcsolót tartalmaz. Pl. ideiglenesen kiiktathatjuk a lapok megjelenítését, ha a már megrajzolt lapok akadályozzák, hogy szemügyre vegyük az egyes pontokhoz tartozó sorszámokat. (Bár a lapok megjelenítése letiltható a Live 3D megjelenítõ Detail menüpontjának a megfelelõ alkalmazásával is.)
Ha már van legalább egy lapunk, válasszuk azt a megjelenítési módot, amelyet bekapcsolva "csak az a lap látszik, amelynek a képe pozitív körüljárású". Ezzel elérhetjük, hogy minden lap körüljárási iránya ugyanolyan legyen. Ha ez valamely lapra még sem teljesül, nem kell azt kitörölnünk és újra felvennünk, a lapok szerkesztése közben a + , ill. - billentyûvel megváltoztatható a pontok sorrendje. Hasonlítsuk össze - megmozgatva az alakzatokat - ezt a két bemutatott példát.
A lapokat megadva egy - egy lap színét elõször a program által felkínált színek közül választottuk. A program "színek megadása" menüpontja lehetõséget ad arra, hogy a színeket átdefiniáljuk, más- más színt rendelve egy-egy sorszámhoz. Az így kapott színeket megvizsgálhatjuk a képernyõn is, amennyiben a szín beállításakor kértük az ilyen program elõállítását.
A program egyik legjobban kihasználható lehetõsége a "Koordináta transzformációk" által nyújtott lehetõség. Ezzel az alakzatunkat alávethetjük egy tetszõleges hasonlósági (egybevágósági) transzformációnak, így nem csak az alakzat koordinátarendszerben elfoglalt helyét változtathatjuk meg, hanem elõállíthatjuk (egy negatív hasonlósági együtthatóval) a centrális tükörképét is. (Ez a rajz egy centrális tükrözés, valamint egy X tengely körüli 180 fokos elforgatás eredményeként jött létre.)
A program lehetõséget nyújt arra, hogy a (megfelelõ koordináta transzformációkkal elõkészített) fájlokat összefésülje egyetlen geometriai alakzattá, amennyiben a két alakzatnak együtt sincs több mint 250 csúcsa, éle, vagy lapja. Ez az ábra is így jött létre, természetesen elõbb mindkét alakzatot alá kellett vetnünk egy eltolásnak.
A geometriai transzformációk és a fájlok összefésülése réven megkímélhetjük magunkat egy - egy bonyolultabb, de valamilyen szimmetriát tartalmazó geometriai alakzat adatainak az egyenkénti beírásától. Vizsgájuk meg ezt a lehetõséget egy bonyolultabbnak tûnõ, de alapjában véve egyszerû példán.
Állítsunk elõ egy félig-szabályos poliédert, az un. arkhimédészi kockát, melynek minden csúcsába egy négyzet és négy szabályos háromszög illeszkedik! (Az itt bemutatásra kerülõ VRML jelenetek a szóban forgó program korlátozás nélküli változatával készültek. A fájlok a demo változattal is beolvashatók, a tárgyalt mûveletek ezzel is végrehajthatók, csak a kapott eredményt nem tudjuk menteni, így megnézni sem.)
A program szerzõje és e sorok írója nem szégyelli bevallani, hogy matematika tanár, s mint ilyen, rendelkezik némi - talán nem is kismértékû - szakmai elfogultsággal. Az itt bemutatott geometriai konstrukciót érdekesebbnek, talán látványosabbnak is véli a képernyõn viaskodó zöldfülû szörnyetegeknél. Bocsássa ezt meg neki a kedves olvasó! E személyes kitérõ után lássunk munkához.
A poliéder lerajzolása - pontosabban a koordináták megadása - némi matematikai (térgeometriai, algebrai) megfontolást igényel. Akit kevésbé érdekelnek ezek a a kérdések, ugorja át ezt a részt, amely nem tartozik szorosan a témánkhoz, a továbbhaladáshoz elegendõ a vizsgálódás eredményét ismerni.
Ez a poliéder lényegében úgy származtatható a kockából, hogy a kocka lapjaira rajzolunk a kocka lapjával azonos középpontú kisebb négyzeteket, amelyeknek kissé elfordítunk valamelyik - de minden lapra vonatkozóan azonos irányba - úgy, hogy a szomszédos lapokra illeszkedõ csúcsok éppen szabályos háromszögeket alkossanak.
Legyenek az XY síkkal párhuzamos helyzetû négyzet A csúcsának a koordinátái A ( x, y, 10), Ekkor a B, ill. C csúcs koordinátái B( -y, x,10 ) és C( y, 10, x) . (A befoglaló négyzet csúcsai: (10,10,10), (-10,10,10) ... stb- .)
Úgy kell megválasztanunk x és y értékét, hogy az ABC háromszög szabályos legyen. Rendre felírva az AB , AC és BC szakaszok távolságát, x -re és y -ra egy (sajnos harmadfokú egyenletre vezetõ) egyenletrendszert kapunk, melynek közelítõ gyökei: x=5.43689 , ill. y=2.9559 .
Ha már tudjuk az xy síkkal párhuzamos, attól 10 egységnyire lévõ négyzet egy csúcsának a koordinátáit, kezdhetjük a munkát a négyzet további csúcsainak a felvételével. Íme az eredmény: A1.wrl A könnyebb tájékozódás érdekében megjelenítettük a befoglaló kocka egy lapjának az éleit is. Több pontot nem is kell "kézzel" felvennünk, ezekbõl egybevágósági transzformációkkal és az egyes fájlok összefésülésével kialakítható az alakzat összes csúcsa.
A koordináta transzformációk menüpontot aktivizálva az alábbi mûveleteket kell rendre elvégeznünk:
Most az elõzõekhez hasonló módon ismét az A1 fájlból kiindulva érjük el, hogy a forgatás tengelye az X tengely legyen, majd helyezzük a (0,0,1) pontot az Y tengelyre. Ezzel megkapjuk az A5 alakzatot. Ennek az X tengely körüli 180 fokos elfordításával - amelyet pl. úgy érhetünk el, hogy a (0,-1, 0) ponthoz az Y tengelyt választjuk ki - eljutunk az A6 fájlhoz.
A keresett poliéder összes csúcsát megkapjuk, ha - miután ismét kiürítettük az adatbázisunkat - rendre beolvassuk és összefésüljük az A12 , A34 , A5 és A6 fájlokat. Így jutunk a B.wrl fájlhoz. A csúcsok sorszámozását természetesen befolyásolja a beolvasás sorrendje. A keletkezett fájl "megjelenítés " c. menüpontjában beállítható tulajdonságai megegyeznek az utoljára beolvasott fájl tulajdonságaival. A program gondoskodik arról, hogy ugyanaz (vagy egymáshoz igen közeli) csúcs, valamint az ugyanazokat a pontokat összekötõ szakasz csak egyszer szerepeljen az adatok között. Ugyanakkor nem vonja össze az egybeesõ lapokat. Ezért ahhoz, hogy a poliéder háromszöglapjait is a már alkalmazott transzformációkkal vegyük fel, a hat négyzetlap közül ötöt el kell távolítanunk. Helyette a megmaradó négyzetlaphoz élben csatlakozó háromszöglapokat vegyük fel a " lapok megadása" menüponttal. A megfelelõ csúcsok sorszámait a B.wrl ábráról célszerû leolvasnunk.
Az így kapott B1.wrl alakzattal ugyanazokat a transzformációkat és összefésüléseket végezzük el, mint az A1 .wrl alakzattal. Lényegtelen, hogy a lapokra nem illeszkedõ csúcsokat és éleket letöröljük-e vagy sem. Az összefésülések során ezek nem adnak új pontokat. Eszerint ugyanezt az eredményt kapnánk, ha a "letisztított" B11.wrl fájlból indulnánk ki. Természetesen ekkor más sorszámot kapnának ugyanazok a pontok. Az viszont fontos lehet, hogy bekapcsoljuk a körüljárási iránytól függõ megjelenítést. Ezzel ellenõrizhetjük, hogy jó sorrendben vettük-e fel egy-egy lap csúcspontjait.
Így kapjuk rendre a B2.wrl , B12.wrl , B34.wrl , B5.wrl , B6.wrl fájlokat. Az utóbbi négy fájlt rendre összefésülve kapjuk a B123456.wrl fájlt, amelybõl már csk a azok a háromszöglapok hiányoznak, melyek csak egy csúcsukkal csatlakoznak a négyzetekhez. (Mivel a B1.wrl fájl tulajdonságait úgy állítottuk be, hogy csak a jobbsodrású lapok legyenek láthatóak, ezért a B123456.wrl fájl is ilyen lett. A koordináta transzformációk biztosították, hogy minden lapon helyes legyen a csúcsok körüljárási iránya.)
Miután elõállítottuk a B2 és B5 fájlokat, az ezeket (is) felhasználó többi fájl elõállítása elõtt megváltoztattuk a lapok színét, már jó elõre arra gondolva, hogy a kész poliéder lapjait miként szeretnénk színezni.
Aki úgy érzi, hogy bonyolultabb munka a koordináta transzformáció, mint a hiányzó nyolc háromszöglap felvétele, az a B123456 alakzatról leolvashatja a hiányzó lapok csúcsainak az indexei, ezeket beírva már meg is kapja a keresett poliédert. A leolvasáshoz célszerû ideiglenesen kikapcsolni a lapok megjelenítését, így minden sorszám láthatóvá válik.
A forgatás és összefésülés lehetõségeivel élve viszont elegendõ pl. a hiányzó háromszögek közül kettõt felvennünk csúcsaik sorszámai alapján, ismét a B.wrl alakzatból kiindulva. Igy kapjuk - a négyzetlapokat letörölve - a C1.wrl fájlt, ebbõl pedig a már megszokott mûveletekkel rendre a C2.wrl , C12.wrl , végül a C34.wrl fájlokat. A két utóbbit összefésülve a B123456.wrl alakzattal, az archimédeszi kocka végsõ alakzatát kapjuk D1.wrl , amelyet azonban meg kell szabadítanunk a szerkesztés kedvéért felvett "sallangoktól".
Munkánk eredménye a keresett arkhimédészi kocka, melyrõl - más szempontok szerint körüljárva a témát - itt is olvashatnak.