Bármely összefüggő, beágyazott, síkbeli G gráf definiálható egy duális G* gráffal, csúcsot rajzolva G minden lapközéppontjába, és összekötve két szomszédos lapon lévő csúcsokat egy e* vonallal, áthalad a közös e élen. Megjegyzem, hogy G**=G. Bármely G-beli kör - Jordan vonal tétele alapján - elkülönül G*-tól. G bármely aciklikus F részgráfja erdő, és nincs kapcsolatban G*-gal (azaz F bármely lapjáról el lehet jutni bármely másik lapjára fák körüli kerülőúttal). Így az összefüggőség és az aciklikusság egymás duálisai. Ezen dualitás alapja a következő bizonyítás:
Bármely átfogó T fa kiválasztásával G-ben definiálhatunk összefüggő aciklikus részgráfot. A duális élek ennek komplemetere, (G-T)*, azonos egy aciklikus összefüggő G*-beli részgráffal, ezért G* is átfogó fa. A két fának együtt összesen (V-1)+(F-1) éle van.
Ez a kedvenc bizonyításom, és ez az egyetlen, amit használok, amikor gráfelméletet tanítok. Sommerville Von Staudt-nak tulajdonítja. Jól illeszkedik más síkbeli dualitások témakörébe, mint például az a tény, hogy minden síkbeli gráf - annak összes lapjával együtt - kétoldalú (az Euler vonal dualitása alapján). Az Euler formulára vonatkozó különböző egyéb bizonyításoknak két változatuk van, egy az eredeti gráfban és egy annak duálisában, de ez a bizonyítás önmaga duálisa ugyanúgy, mint ahogyan maga az Euler formula is az.
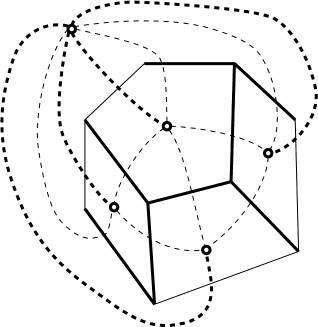
Hasznosnak bizonyult az ötlet - miszerint bontsuk szét a gráfot összefonódó fákra - az algorimusok számát tekintve, magába foglalva saját munkámat és mások munkáit is a dinamikus minimális átfogó fákkal kapcsolatosan, ugyanolyan jól dolgozik, mint Goodrich és Tamassia pontrögzítő módszere. Kézenfekvő összakapcsolni a VLSI tervezéssel és a vízválasztó vonalak elemzésével.
Lapok szerinti teljes indukciót használva bizonyítani tudjuk a formulát minden összefüggő, síkbeli G gráfra.
Ha G-nek csak egy lapja van, akkor az aciklikus (Jordan vonal tétele alapján) és összefüggő, így fa és E=V-1. Különben válasszunk egy e élt, amely összeköti G két különböző lapját, majd távolítsuk el. Látható, hogy a megmaradó gráf összefüggő lesz - bármely olyan út, amely magába foglalta e-t, kicserélhető egy olyan úttal, amely út a két kölönböző lap egyik oldala körül. Ez az eltávolítás egyel csökkenti mind a lapok mind az élek számát, és az eredmény az indukció alapján következik.
Ez a bizonyítás általában megtalálható gráfelmélettel foglalkozó tankönyvekben (példának okáért Bondy and Murty), de ez a számomra legkevésbé kedves bizonyítás, mivel feleslegesen komplikált és nem kifinomult, a teljes indoklás egyes lépései olyan nehéznek látszanak, mint az egész első bizonyítás. Nem jól általánosítható, és van néhány kritikus részlete, amit a tankönyvek szerzői gyakran elhagynak.
Ez az érvelés síkbeli duálisa a lapok szerinti teljes indukciós bizonyításnak.
Ha G-nek csak egy csúcsa van, akkor minden éle Jordan vonal, így E+1 lapja van, és F+V-E=(E+1)+1-E=2. Különben válasszunk egy e élt, amely összeköti G két különböző csúcsát, és húzzuk össze azokat egy csúcsba. Ez csökkenti mind a csúcsok mind az élek számát egyel, és az eredmény az indukció alapján következik.
A két előző bizonyítást összekombinálva kapunk egy jóval egyszerűbb alapesettel rendekező indukciót.
Ha a G összefüggő, síkbeli gráfnak egyetlen éle sincs, akkor ő egy izolált csúcs, és V+F-E=1+1-0=2. Különben válasszuk ki bármely e élét. Ha e összeköti két csúcsát, akkor húzzuk össze azokat egy csúcsba, így csökken V és E egyel. Különben e egy Jordan vonal, ami két lapra osztja G-t. Eltávolítva e-t, F és E csökken egyel. Egyik esetből - a kettő közül - következik az eredmény az indukció alapján.
Ezt a bizonyítást van Lint and Wilson használta. Egyéb változatok is lehetségesek - ha e összeköt két csúcsot és elválaszt két lapot, akkor e törlésére, vagy összehúzására más módok is választhatók.
Ezt a bionyítást by Alex Bogomolny küldte nekem, aki orosz fordításban fedezte fel (1958) Hadamard: Elemi geometria című könyvének hetedik kiadásának második kötetében. Erősen kapcsolódik a (!!) ear decomposition bizonyításhoz.
A bizonyítás a lapok száma szerinti teljes indukcióval történik. Először eltávolítunk egy lapot és ellenőrizzük, hogy a formula V-E+F=1-et ad, azaz megnézzük, hogy nyitott poliéderfelületet kapunk-e. Egy egyedüli lapra a formula nyilván igaz. Feltesszük, hogy F-nél kevesebb lapra is igaz a formula, és belátjuk F-fel megegyező lapszámra is. Vegyünk ki két csúcsot a felület határáról (balra az eltávolított laphoz képest), és csatlakoztassuk őket láncszerűen belső élekhez. (Ilyen lánc mindig kialakítható a Jordan vonal tétele alapján.) Most vágjunk tovább a lánc mellett. Kapunk két felszínt, amelyekre a formula V-E+F=1-et ad. Az első legyen V1-E1+F1=1, a második pedig V2-E2+F2=1. Feltesszük, hogy a lánc tartalmazz L élt és mostantól (L+1) csúcsot. Ebből következik, hogy E1+E2=E+L és V1+V2=V+L+1. Természetesen F1+F2=F. A kettő algebrai összege megadja a kívánt eredményt.
Használható a bizonyítás duálisa is, amikor egy nyitott lapot szétszedünk (kezdetben csúcsot távolítva el a poliéderből) egymás után váltakozva éleire és lapjaira.
Ez a bizonyítás Thurston-tól származik. Ezt írja:
Rendezzük a poliédert úgy, hogy egyik éle se helyezkedjen el vízszintesen - mégpedig úgy, hogy pontosan egy U legfelső és pontosan egy L legalsó csúcsa legyen.
Helyezzünk + töltést minden csúcsba, - töltést minden él felezőpontjába, és + töltést minden lapközéppontba. Megmutatjuk, hogy a töltések semlegesítik egymást, kivéve L és U csúcsokat. Ehhez minden csúcsot és az élek töltéseit elmozdítjuk, hogy nekiütközzenek a szomszédos lapnak, ezután összecsoportosítjuk minden lap összes töltését. Mivel a mozgás irányítását meghatározza az a szabály, hogy minden töltés vízszintesen mozog, az óramutató járásával ellenkező irányban, ahogyan ez felülnézetben látható.
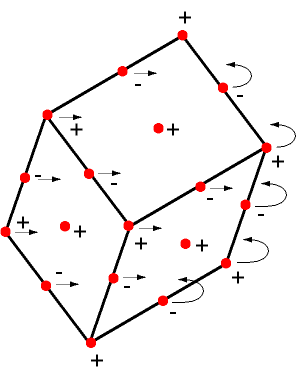
Így végül minden lap kap töltést a nyitott intervallum határa mentén. Ez a nyitott intervallum felváltva szétszedhető élekre és csúcsokra. Amikor már csak az első és az utolsó csúcs marad, akkor egy - töltéstöbblet van, következésképpen az összes töltés minden lapon nulla. Végül az L és U csúcsok együttesen +2 töltést adnak.
Thurston folytatta az ötlet általánosítását az Euler karakterisztikára vonatkozó tétel bizonyításában.
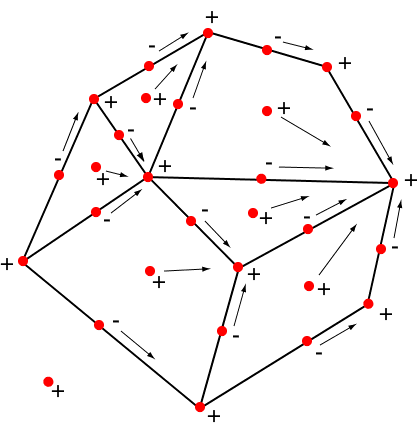
Inkább laponként csoportosítsuk a töltéseket a gráfban. Ekkor a csúcstöltések csoportosításának duálisát kapjuk. A bizonyítás konvex, síkbeli, poliéderbe beágyazott gráfra működik legjobban.
Ha szükséges, forgassuk el úgy a gráfot, hogy ne legyen függőleges éle. Miként az előző bizonyításban, helyezzünk + töltést minden csúcsba, - töltést minden él középpontjába, és + töltést minden lapközéppontba. Megmutatjuk, hogy - két + töltés kivételével - a töltések semlegesítik egymást. Ehhez - a legjobboldalibb csúcs felé haladva - minden él jobb végpontjába mozgatjuk a töltéseket (kivéve a külső lapot). Minden csúcs (kivéve a legbaloldalibb) váltakozó sorrendben kap töltéseket az élektől és a lapoktól, semlegesítve ezzel a kezdő töltésüket. Az egyetlen megmaradó nem semlegesített + töltés a külső lapon van, és persze megmarad a legbaloldalibb csúcs töltése is.
Ez a bizonyítás azon a tényen alapul, hogy síkbeli gráfok megadhatók beágyazott poliéderekkel, így minden élük megfeleltethető egyenes szakasszal.
Egyenes vonalak rajzolásával a gráfban adjuk össze az összes lapon található szögeket (beleértve a külső lapot is). Az szögek összege k oldalú poligon esetén (k-1)pi, és minden élt két laphoz adtunk hozzá, így a teljes összeg (2E-2F)pi.
Most másképpen számoljuk meg az azonos szögeket. Minden belső csúcs háromszögekkel van körülvéve, és ez a teljes szögösszeghez 2 pi-t hozzáad. A külső lap csúcsainál lévő szögeknél 2(pi - theta(v)) az összeg, ahol theta jelöli a sokszög külső szögét. A teljes külső szögösszeg minden sokszög esetén 2 pi, így a teljes szögöszeg 2 pi V - 4 pi.
A két formula összekombinálásával és osztva 2 pi-vel, megkapjuk a V - 2 = E - F összefüggést, ami ekvivalens a V-E+F=2 formulával.
Sommerville ezt a bizonyítást Lhuilier-nek és Steiner-nek tulajdonítja. Hilton és Pederson ugyanígy háromszögeket használt és összefüggésbe hozták a poligonok felületének Euler karakterisztikáját a teljes szögdefektusával.
Ez a bizonyítás szögek összeadásával működik, felhasználva a szferikus háromszögelés feltéveleit, jőval egyszerűbb, mert ez a szabályokba foglalás nem kezeli külön a külső lapot, így nem bonyolítja a bizonyítást.
Szükségünk van a következő egyszerű tény kimondására a gömbháromszögtanból: ha 4 pi-ben normalizáljuk a gömb felszínét, és megvizsgáljuk, hogy bármely háromszög megadható gömbi főkörívekkel, a háromszög három belső szöge pi+a (a háromszög többlete, defektusa), ahol a megegyezik a háromszög területével. (lásd Wells, 238. oldal).
Ahhoz, hogy értelmezzük a sokszögre vonatkozó kérdésünket a gömbi geometriában, először osszuk háromszögekre a poligonunkat. Minden új él növeli E-t és F-et egyel, így V-E+F változatlan marad. Most végezzünk el egy - a címlapon leírthoz hasonló - fény-árnyék kísérletet. Helyezzünk el egy fényforrást a poliéder belső pontjában, és a poliéder külső gömbi ernyő fényforrása olyan, mintha a középpontja lenne. Az árnyék vetülése a poliéder éleit gömbháromszögként mutatja. Mivel minden él két háromszöghöz tartozik és minden háromszögnek három éle van, így 2E=3F.
Adjuk össze az összes háromszög szögeit, ahogyan a gömbháromszögtan megadja, az összeg (4+F) pi. Összegezzük másképpen ugyanezeket a szögeket, minden csúcsnál, 2 V pi összeget kapunk. Mivel a két összeg ugyanazokra a szögekre vonatkozik, F=2V-4 és a másik egyenlettel összevetve az adódó eredmény 2E=3F lesz.
Sommerville ezt a bizonyítást Legendre-tól származtatja. Mivel összekapcsolható a geometriai topológiával, ezt a bizonyítást Weeks használta, aki egy elegáns bizonyítást adott a szferikus szögterületre vonatkozó összefüggéssel kapcsolatban, ami a kör alakú kettős ékek hozzávételén és kihagyásán alapul.
Az A*k=2 pi (V-E+F) összefüggésben a k görbületi konstans, megtalálható a Gauss-Bonnet formulában, a differenciálgeometria témakörben.
Ha átültetjük a szögek összegére épülő bizonyítást a gömbháromszögtanba, akkor a folyamat során a formulák a lapok területösszegére vezetnek. Most megvizsgálunk egy hasonló területösszeggel kapcsolatos formulát a síkgeometriában. Wells gondolatmenete következik.
Pick elméletének alapeszköze: Legyenek a csúcsok koordinátapontjai (x,y), ahol x és y egészek. Ekkor a P poligon területe kifejezhető N + B/2 - 1 alakban, ahol N az egész belső pontok száma, és B pedig P élei és csúcsai egész pontjainak száma. Ez bizonyítottan adja a következő lehetőséget: például válasszunk egy vízszintes L vonalat, amely a poligon alsó részén halad, és elválasztja a poligonok területét adó trapézok előjeles területösszegeitől L minden élét. Ez a bizonyítás nem szükséges az Euler formulához, így nem veszélyes a körbenjáró gondolkodás.
Először rajzoljunk egy poligonnal egyező síkbeli gráfot, legyen minden éle egyenes. Ha lehetséges, akkor válasszunk eléggé kicsi r sugarat, mozgassunk bele minden csúcsot valahová a kör belsejébe úgy, hogy a középpontja az eredeti helyén maradjon, az eredménygráf síkbeli lesz, méretezzük úgy a gráfot, hogy r=1 legyen. Ezután mozgassunk minden csúcsot a hozzá legközelebbi egész csúcshoz, az eredmény ekvivalens lesz egy síkbeli rácskoordinátákhoz rajzolt gráffal.
A gráf külső lapja egyszer pontosan lefedett a megmaradó lapokkal, így az eltávolított lapok területösszege meg kell egyezzen a külső lapok területével. Pick elmélete szerint aez I+X+B/2+S/2-(F-1), ahol I az egy lapon lévő egész belső pontok száma, X a belső éleken lévő pontok száma, S az összes olyan belső lap száma, amelyhez a csúcsok hozzátartoznak.
A gráf belső csúcsai hozzáadó feltétel megadja S fokát, ahol külső lapon lévő csúcsok csak a fokszám -1-et adnak hozzá. Ebből S=2E-K következik, ahol K a külső lapon lévő csúcsok száma. Egyébként Pick elméletében a külső lap területe (I+X+V-K)+(B+K)/2-1. A két egyenlet S=2E-K és I+X+B/2+S/2-(F-1)=(I+X+V-K)+(B+K)/2-1 kifejezéseket eredményezi.
Sajnos Pick elmélete nem általánosítható magasabb dimenziókba, így ez az elképzelés nem hasznos a magasabb dimenziójú Euler formulák használatánál.
Bármely él eltávolításával a gráf két él által összefüggővé tehető - részgráf. A két él kapcsolat ekvivalens a fogantyú dekompozíció létezésével: a gráf éleinek felosztása sorfolytonosan fogantyúkra (egyszerűen utak és körök), az első fogantyú egy egyedülálló csúcs; az elejétől a végéig minden egymás után következő fogantyúnak rá kell épülnie az előző fogantyúkra, de az összes többi csúcsnak újnak kell lennie a fogantyún. Ez a dekompozíció (felbontás) egyszerre egy fogantyút talál: minden fogantyú elejétől indulva a még nem felhasznált e éltől a már felfedezett csúcsig, és folytatva a legrövidebb úton vissza egy másik már felfedezett csúcshoz (ilyen út létezik, mivel e nem izolált él a gráfban).
Ilyen dekompozíciót használunk a poliéderekre vonatkozó Euler formula bizonyításában:
A poliéder G gráfja két él kapcsolatú, mivel ha egy e élt eltávolítunk, akkor még az ő végpontjainak összekötésével utat kapunk a túlsó oldal körül a gráf két lapja között.
Keressünk fogantyú dekompozíciót G-ben, gondoljuk végig a G átalakítás folyamatát fogantyúk hozzáadásával, a kezdettől - egyedülálló csúcs. Kezdetben van egy csúcs, egy lap és nincsenek élek. Minden új fogantyú ad egy utat, amely összeköt két csúcsot a lap határán, felbontva azt két lapra; az út legalább egyel több élt tartalmaz, mint ahány csúcsot. Így, ha a fogantyúnak k csúcsa van, A hozzáadás növeli V-t k-1-el, E-t k-val, és F-et 1-el és az eredmény következik a fogantyk száma szerinti teljes indukcióval.
A fogantyú dekompozíció különösen hasznos a párhuzamos algoritmusok tervezésekor, párhuzamosan könnyebben kereshetünk, mint más strukturális dekompozícióval a gráfokban, úgymint a fákban használható mélységi keresés. Erre például megtekinthető egy munkám a felismerő sorozatok párhuzamos gráfokkal kapcsolatosan.
Ziegler interpretálta a poliédert vagy politópot, mint komplex poliédrikus lapokat, változó dimeziókban. Megjelölve fi-vel a lapok számát az i dimenzióban, megkapjuk, hogy f0=V, f1=E, és f2=F, de ő még hozzáadja a d dimenzió lapjait (az egész politóp) és -1 (az üres lap), így f-1=fd=1. Ziegler definíciója szerint a komplex poliédrikus lapok lehámozása lineáris sorrendű a maximális dimenziójú lapokon, hasonlóan ha a lapok dimenziója legalább egy, a sorrend teljesíti a következő két tulajdonságot:
Minden konvex politópnak van lehámozása, ez megtalálható egy egyenes vonalon kiindulva néhány olyan pontból, amelyek a poliéder egy lapján helyezkednek el és sorrendbe állítva a lapokat, ahogyan a pontok követik egymást, így a vonal áthalad a lapok síkján és a lap láthatóvá válik. (A vonalat úgy kell elképzelni, hogy elmegy a végtelenbe és visszatér miközben áthalad a poliéder másik oldalára.) A lapok metszete Fj az vonal a lapok síkjára nézve a metszéspontokat láthatóvá teszi, ez megmutatja, hogy szükséges-e alacsonyabb dimenziójú lehámozás (2. tulajdonság). Ziegler a dimenzióra vonatkozó lehámozás hossza szerinti teljes indukcióval igazolja, hogy bármely politópnak van Euler karakterisztikája és az pedig X(P)=Sum(-1i fi)=0:
Az alapeset, amikor f-1=f0=1 triviális. Ha P egy d-politóp, akkor a lehámozás sorrendje F1,F2,..., precízebben X(F1 u F2 u ... u Fj) 0 j < fd-1-től 1 j = fd-1-ig, ami j szerinti indukciót jelent, amikor a hozzáadott lapok (d-1)-politópok. Az Euler karakterisztika additív, és az Fj-k metszete, mivel j < fd-1 nem üres (Ziegler megmutatja, hogy ez utóbbi megfigyelés áltatában igaz, de geometriailag következik a lehámozás fenti definíciójából is).
Eltávolítva a két "extra" f-1 és f3 lapot ebből az összegből megkapjuk a szokásos Euler formulát.
Ez a bizonyítás csak egy variációja a lehámozásnak, de történelmi jelentősége van: Cauchy használta és Lakatos hosszasan megvizsgálta.
Kezdjük egy poliéder éleinek konvex síkbeli rajzolásával. Ha tartalmaz nem háromszögből álló lapot, akkor húzzuk be a lap átlóját, ezzel felosztottuk két részre, és növeltük az élek és lapok számát, az eredmény a teljes indukcióból adódik.
Tegyük fel, hogy bármely síkbeli gráfnak minden belső lapja háromszög alakú, van legalább két lapja. (Poliéderünk konvex háromszögelése egyszerűen teljesíti erzen tulajdonásgokat.) Mindig van legalább két háromszögünk, amelynek élei a határon vannak, így egyik eltávolítása után egyetlen háromszög marad vagy a gráf azonos típusú kisebb gráf lesz. Ez a háromszögek száma szerinti teljes indukció. Ha néhány határos háromszög elválaszt belső pontokat, akkor a két elválasztott komponensen lesz két nem határs él, ami miatt egyikük egyedülálló háromszög (ami eltávolítható) vagy van két eltávolítható határos háromszögünk (indukcióval), és legalávv egyiküket eltávolítjuk a teljes gráfból.
Így, határos háromszögek egyenkénti eltávolításával minden lépésben eltávolítunk egy élt vagy egy lapot, vagy két élt, egy lapot és egy csúcsot. Az összes esetben V-E-F változatlan marad. Végül kapunk egy egyedüláll háromszögből álló gráfot, amelyre V-E+F=3-3+2=2.
Az esetanalízis használható magasabb dimenziójú változatban is, ez a bizonyítás szorosan kapcsolódik Radon elméletéhez, amelyben d+2 pont elválasztására kerül a sor, ez pedig konvex hurok metszetnek két részhalmaza és algoritmusa alapul szolgál Delaunay háromszögeléséhez.
A bizonyítás részleteit Bishop és Goldberg adta meg.
Definiáljunk egy poliéder felületi magasságfüggvényt az alábbiak szerint:
Válasszunk tetszőleges magasságot minden csúcshoz. Minden élen válasszunk egy olyan belső pontot, amely magasabban van, mint a két végpontja, és lineárisan interpoláljuk az él maradékához, a kiválasztott pont és a végpontok közé. Minden lapon válasszunk magasságot belső pontnak, magasabbat, mint az összes határán lévő (szomszédságában), lineárisan interpoláljuk a magasságokat a maradék lapokhoz, a kiválasztott ponttól a határig. Az eredmény egy folytonos függvény V+F+E kritikus pontokkal: V lokális minimuma a csúcsoknál, E nyerge a kiválasztott élek pontjainál, és F helyi maximuma pedig a kiválasztott lapok pontjai lesznek.
Most nézzük a felületet: kezdetben teljesen száraz föld, amelyre özönvíz zúdul, amely teljesen elfedi a legmagasabb hegycsúcsát is. Számoljuk meg a tavakat, és kapcsoljuk hozzá a kialakult földtömeghez, és romboljuk le egy özönvízzel, hogy elérjük az eredményt.
Minden helyi minimum egy-egy tónál található. Minden nyereg vagy két tó összekapcsolódásával, vagy egy egyedülálló tó leapadásával elválasztódik egy földtömegtől (jelöljük J-vel és D-vel azon idők számát, amikor ezen események megtörténnek). Minden egyes hegycsúcsot eltöröltünk. Kezdetben volt egy földtömegünk és végül kaptunk egy az egész világra kiterjedő tavat. Így 1+D-F=0 és 0+V-J=1, amelyekből végül eredményként D+J=E adódik.
Láthatjuk, hogy a természetellenes esőzés okán, a globális vízállás mindenhol ugyanannyi, így ha veszünk két tavat, amelyek egyszerre érnek el egy hágót, vagy találunk egy valószerű nézőpontot, akkor elmondhatjuk, hogy az esőzés tetszőlegesen megváltoztatta a bolygót, de amíg egy tó eléri a hágót, akkor a víz túlcsordul (és a tó vize nem emelkedik tovább) amíg a hágó másik oldalán lévő tó el nem éri ugyanazt a magasságot.
A bizonyítás önmaga duálisa, a legnagyobb asszimmetriát a magasságfüggvény definíciója adja. Szokás szerint, Jordan vonal tétele magába foglalja, és valóban a tavak leapadásával szigetek keletkeznek.
Az alábbi bizonyítás részletei Lakatostól származnak (aki Poincaré érdemének tartja), Lakatos kihagy belőle néhány részletet a b leképezés alábbi jellemzőjéből, ehelyett ezeket axiómaként kezeli (így végül bebizonyítja, hogy az Euler formula igaz bármely olyan poliéderre, amelyra ugyanezek axiómáknak tekinthetők, azonban nem bizonyítja, hogy igaz bármely konvex poliéderre).
Miként a lehámozásos bizonyítás, ez is komplex poliédrikus lapokat interpretál poliéderként vagy politópként változó dimenziókban, definiálva fi-t, mint a lapok száma az i dimenzióban. Ugyanúgy itt is kapunk két "extra" lapot, egyet a teljes politópra, és egyet mint üres lap, így f-1=fd=1.
Adjuk meg az i dimenzió lapjainak részhalmazát, mint egy vektortér feletti kételemű GF(2), és a vektorok összeadását adjuk meg, mint részhalmazok szimmetrikus differenciája (közismertebben kizáró vagy). Így kapjuk d+1 darab Vi vektorteret, amelyeknek dimenziója egyenlő fi-vel. A politóp lapjainak halmaza interpretálható e vektorterek bázisaiként.
Ezen terek előállíthatók b lineáris leképezéssel minden egyes Vi tértől a következő alacsonyabb dimenziójú térig, minden lapra definiálható. Amikor v a lapok összege, b(v) a megfelelő lapok halmazának összege. (Az üres lapnak nincs oldala.) Ezen leképezés fontos jellemzői:
Ennyi előkészület készen állunk bebizonyítani, hogy Sum(-1i fi)=0.
Legyen Bi a Vi egy altere, amely b(v)=0 vektorokat tartalmazza. A b leképezés Vi-t Bi-1-be viszi. Hacsak a vektorterek lineáris leképezéséről van szó, osszuk fel az eredeti teret nulltérre. Ezekből következik, hogy dim(Vi)=dim(Bi)+dim(Bi-1). Kiterjesztve kapjuk, hogy Sum(-1i fi) = Sum(-1i (dim(Bi) + dim(Bi-1))), amely megegyezik 0-val, mivel minden Bi kétszer szerepel eltérő előjellel.
A két extra paraméter - f-1 és f3 - kiküszöbölését követően megkapjuk az Euler formulát.Azt gyanítom, hogy van direktebb, dimenzió nélküli módszer is a bizonyításra, de nem láttam, Lakatos nem írja le.
A Homológiai teória szerint, az algebrai topológia alapköve, definiál hasonló vektortereket, ahol az alapegyenlőség a dim(Vi)=dim(Bi)+dim(Bi-1), és ez más topologikus terekben nem igaz.
A bináris téfelosztás egy gyakran használt adatszerkezet, a számítógépes grafikában és más geometriai keresési problémáknál. Kialalkítható a tér hipersíkokkal való feldarabolásával, amely a keletkező két féltérrészt rekurzívan tovább osztja. Az eredmény: a tér egy hierarchikus dekompozíciója, amely konvex cellákból áll.
1974-ben, Helge Tverberg mutatta nekem a bizonyítást, megadta bármely konvex K politópra. Bináris térfelosztással K egyszerű politóppá alakítható. Nyilvánvaló, két dimenziós politópok esetében (ahol csak ismételt átlóbehúzások és vágások vannak), az általános bizonyítás előáll a dimenzió és lapok szerinti teljes indukcióval:
Tegyük fel, hogy K nem egyszerű, vagy már készen is vagyunk.
Ha K-nak van P véletlenül kiválasztható d oldalához tartozó csúcsa, akkor (dimenzió szerinti indukcióval) felosztható K hipersíkok segítségével kisebb politópokra. Minden kisebb politópnak kevesebb oldala van, mint K-nak. Az oldalak száma szerinti teljes indukcióval rekurzív felosztás adható.
Másrészt tegyük fel, hogy K minden csúcsa egyetlen d véletlenül kiválasztható oldalon van. Legyen P a K olyan csúcsa, amely nem szomszédos másik két F1, és F2 oldallal (ilyenek mindig léteznek az indukcióból adódóan). Legyen L a hipersík azon hipervonala, amely átmegy F1-en és F2-n, és P és L-en keresztül elvágja K-t.
A vágások száma a oldalak számától függően akár exponenciális is lehet.
Klain és Rota küldte nekem ezt a bizonyítást, akik továbbfejlesztették az Euklidészi terek általános elméletének vonatkozó részét. Köszönettel tartozom Robin Chapman-nek, aki segítette megmagyarázni nekem.
Legyen Ud egy függvények feletti vektortér Rd-től R-ig, és Vd egy generált altere Ud. Definiáljuk a chid függvényt, amely leképezi Vd-t egész számmá, a következőképpen:
Mivel D és Sum lineáris operátorok, chi egy lineáris függvény V-ből R-be. Egyszerű dimenzió szerinti indukcióval könnyen belátható, ha f egy tömör, konvex K halmazbeli karakterisztikus függvény, akkor chi(f) = 1. Indukcióval: chi(fz) egy zárt intervallum karakterisztikus függvénye, definíciója: sum D chi(fz), ami 1. Így chi teljesen definiált függetlenül az Rd-beli koordináták választásától.
Ha g a K politóp relatív belsejének egy karakterisztikus függvénye, eleme Vd-nek, akkor egyszerű indukció megadja, hogy chi(g) = (-1)m, ahol m a K dimenziója: Mivel chi független a koordinátarendszertől, feltehetjük, hogy m=d. K minden keresztmetszete önmaga politópja, így chi(gz) szerinti indukcióval adódik az eredmény, mivel (-1)m-1 egy nyitott intervallum karakterisztikus függvénye, és ennek következménye, hogy az összeg és a D operátor egy -1-essel szorzódik
Most kaptunk egy K konvex politópot, és két különböző módon kiszámítottuk a chi karakterisztikus függvényt, felosztottuk K-t diszjunkt részekre. Mivel chi lineáris, az összeg,
1 = sum (-1)^m
Csoportosítva a lapokat dimenzióik szerint, megkapjuk az Euler
formulát:
1 = sum (-1)i fi
ahol az összeg egytől fut K dimenziójáig.
Proofs of Euler's Formula.
From the Geometry Junkyard,
computational and recreational geometry pointers.
David Eppstein, Theory
Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file. Last update: 27 May 2001, 09:24:41 PDT.