Itt már kissé tüzetesebben megvizsgáltuk a kamera néhány tulajdonságát. Ebből a vizsgálatból az derült ki, hogy a szemlélt objektum és a kamera kölcsönös helyzetét megváltoztathatjuk mind a kamerának, mind magának az alakzatnak a mozgatásával (transzformálásával).

Most ezzel az utóbbi kérdéssel fogunk kissé részletesebben megismerkedni, már csak azért is, mert az alakzatoknak a kamerához, ill. más ábrázolt alakzathoz való viszonyát ezeknek az un. koordináta-transzformációknak a segítségével határozhatjuk meg pontosan. Erre pedig bizony elég gyakran szükségünk lehet.

Előre is elnézést kérünk az olvasótól, amiért a téma kapcsán kissé több szó esik a matematikáról, ezen belül a különböző geometriai transzformációkról. Reméljük, nem fog megártani.

Lényegében két olyan geometriai transzformáció van a VRML nyelvben, amely nem változtatja meg az ábrázolt alakzat alakját, ill. méretét. Ez az eltolás és a forgatás.

Pl. - mint már volt róla szó - ha egy alakzat lerajzolását megelőzően beírjuk a

 Translation { translation 7 5 3 }

eltolásra vonatkozó utasítást, akkor az alakzatunk az ő koordinátarendszerében vett eredeti helyéhez képest a ( 7,5,3) pontba kerül. Ezt persze nem feltétlenül érzékeljük. Pl. a p1.wrl és a p2.wrl   vrml fájlokat beolvasva - melyek forrásprogramja p1.txt és p2.txt - a rajzokon először nem érzékelünk semmilyen különbséget. (Most, és a későbbiekben is a megállapításaink a Live3D megjelenítő alkalmazása esetén érvényesek.) Ha azonban a megforgatjuk a gömböt, már érzékelhető a különbség. Az első a saját középpontja körül forog, amely egyúttal a "világ-koordinátarendszer" origója. A másik ugyancsak a "világ közepe" körül forog, amelyhez képest eltoltuk a Z tengely mentén, azaz felénk.

A továbbiakban, hogy könnyebben érzékeljük a "mihez képest mozog " fogalmát, a vizsgált geometriai transzformációk hatását, felveszünk egy stabil koordinátarendszert, amelyet ugyan interaktívan tudunk mozgatni, de mégis tekintsük úgy, mintha ez lenne a "világ-koordinátarendszer". Még a kamerát is ehhez fogjuk rögzíteni. Az "alakzat"-ot ehhez a rögzített koordinátarendszerhez képest fogjuk mozgatni. Ezen a programrészleten legfeljebb annyit módosítunk, hogy - ha szükségesnek véljük - a perspektív ábrázolás helyett az axonometrikust alkalmazzuk. Ajánljuk olvasóinknak, hogy a fájlba belenyúlva időnként ezt (is) tegyék meg.

Példaként itt a p3.wrl alakzat a mely egy 0.5 sugarú gömb a (3, 5, 7) pontba eltolva. Íme a forrásfájl: p3.txt . A továbbiakban a forrásfájloknak csak az "alakzat" -hoz tartozó részét közöljük. Pl. így: p3a.txt .

A könnyebb tájékozódás kedvéért egészítsük most ki az ábránkat egy élvázas téglatesttel, amelynek az élei párhuzamosak a világ-koordinátarendszerrel, egyik csúcsa az origó, másik az előbbi gömb: p4.wrl , és a forrásfájlja: p4a.txt .

Most alkalmazzunk egy újabb - az egész alakzatra vonatkozó - eltolást: p5.wrl ; p5a.txt . Itt jegyezzük meg, hogy az eltolások sorrendje csak akkor cserélhető fel, ha nincs a kettő között rajzolást eredményező blokk (csomópont). Itt pl. a későbbi eltolás csak a gömbre, az előbbi az egész alakzatra vonatkozik.

Másik, a vrml -ben alkalmazható u.n. egybevágósági transzformáció a forgatás. Pl. Ebben a Transform { rotation  2  3  1   -1.3 } - találomra felírt forgatásban negatív, azaz az óramutató járásával megegyező irányba forgatjuk az alakzatunkat 1.3 radiánnyi szöggel egy olyan térbeli egyenes körül, melynek egyik pontja az alakzat origója, másik a (2, 3 1) pont. Itt az eredmény: p6.wrl , p6a.txt .  Az eltolás és a forgatás sorrendje természetesen befolyásolja a rajzot. Az eltérés főként akkor érzékelgető, ha mindkét sorrendet figyelembe véve lerajzoljuk az alakzatunkat. Most előbb a forgatást, majd az eltolást alkalmaztuk: p7.wrl , p7a.txt .Megkülönböztetésül az utóbbi alakzatnál zöldre festettük a gömböt. Nem meglepő, hogy a két alakzat párhuzamos helyzetű, hiszen a két forgatás tengelye párhuzamos, a szögük is megegyezik.

Tűzzünk most ki egy konkrétabban meghatározott célt. Például próbáljuk meg a p4.wrl alakzatunkat - egyetlen forgatással - úgy elforgatni, hogy a gömbünk illeszkedjék az X tengelyre! Ez esetben a forgatás szöge a (7, 5, 3) vektornak az X tengellyel bezárt szöge, vagyis annak a derékszögű háromszögnek a szöge, amelynek a keresett szög melletti befogója 7, az ezzel szemközti pedig az 5 és 3 oldalú, (XZ) síkkal párhuzamos téglalap átlója.

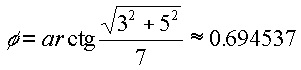
A forgatás egyenese merőleges erre a síkra. Ennek egy pontja lehet pl. a (0, -3, 5) pont. Ha ebből a pontból néznénk a forgatás síkjára, akkor a forgás szögét negatívnak, azaz az óramutató járásával megegyezőnek látnánk: p8.wrl  . Ez a forgás valóban az X tengelyre helyezte a gömbünket: p9.wrl  ,   p9a.txt .

Most oldjunk meg egy kissé összetettebb feladatot. Forgatással illesszük a gömböt a  Z tengelyre úgy, hogy a forgatás eredményeképpen az alakzatot alkotó téglatestnek az Y tengellyel párhuzamos élei továbbra is látsszanak függőlegesnek. Mintha elforgatnánk az alakzatot - tulajdonképpen a vizsgált tárgy koordinátarendszerét - a függőleges Y tengely körül, majd az origón átmenő vízszintes egyenes körüli újabb forgatással magunk felé döntenénk a kívánt mértékben.

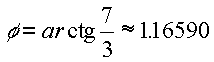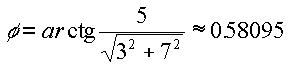Az előzőekhez hasonlóan okoskodva az első forgatás szöge , tengelyének egy pontja pl. a (0, 1, 0) pont, a forgás iránya ismét negatív: p10.wrl . A második forgatás szöge , egyenese az első forgatás után a képernyő síkjában fekvő vízszintes egyenes. Ennek egy pontja lehet pl. a (3, 0, -7) pont, amelyből nézve pozítív a forgásirány: p11,wrl   p11a.txt .

Ezt a két forgatást azért volt érdemes megismernünk, mert így kapunk egy alakzatról olyan (akár perspektív, akár axonometrikus) képet, mint ha az egy vízszintes síkon állna, amelyre kissé rálátunk. Több olyan 3D -s alakzat megjelenítésével (is) foglalkozó program van - pl. a legismertebb matematikai programok egyike a MAPLE - amely pontosan ennek a két forgatásnak a szögét adja meg változtatható paraméterként. Ez a két forgás elegendő ahhoz, hogy bármilyen helyzetbe beállíthassuk az alakzatunkat.

A fentiek illusztrálására bemutatunk egy "kisipari" módszerekkel készült (Pascal) programot, amely egyúttal példa arra, hogy a 3D-s alakzatok megjelenítéshez nem feltétlenül szükséges nagy apparátus. Javasoljuk, az olvasónak, hogy töltse le, majd futtassa ezt a programot: 7lap.exe

Végül oldjunk meg egy egészen általános - egyetlen forgatással megoldható - feladatot. vegyünk fel egy új (zöld) gömböt, amelyet eltolunk találomra , pl. a (-2, 1, 4) pontba. (Mivel a két gömböt külön elválasztó blokkba tettük, a két gömbre vonatkozó eltolás nincs egymásra hatással.)

Próbáljuk most ezt az utóbbit elforgatni úgy, hogy az origó, az első gömb, valamint a második elforgatottja essen egy egyenesbe. Lényegében azt a forgatást kell megadnunk, amellyel egy tetszőleges vektor egy ugyancsak tetszőleges másikkal egy irányba hozható. Ehhez ki kell számolnunk a forgatás tengelyének egy pontját, valamint a forgatás szögét. Ez bizony kissé komolyabb matematikai apparátust igényel. (Akit ez kevésbé érdekel, vagy éppenséggel ismeri, használni is jól tudja az itt bemutatott matematikai fogalmakat, tekintse meg az eredményt: p12.wrl , p12a.txt , és ugorja át ezt a csöppet sem kellemes, de a matematika iránt (is) érdeklődők számára talán hasznos részt.

Két, általános helyzetű, térbeli koordinátáival - azaz egy-egy ponthármassal - adott vektor szögének a meghatározására egyik legkönnyebben, minden esetben alkalmazható módszer egy a középiskolából ismert fogalmat, a vektorok skalárszorzatának a fogalmát használja.

Az a és b vektorok skalárszorzatán - melyet (ab) -vel jelölünk a két vektor hosszának, valamint az általuk bezárt szög koszinuszának a szorzatát értjük:

Mivel két vektor szögét úgy értelmeztük, hogy az nem nagyobb az egyenesszögnél, ezért a szög koszinusza egyértelműen meghatározza magát a szöget. Ha két vektor egyike sem null-vektor, akkor skalárszorzatuk akkor és csak akkor lesz 0 , ha merőlegesek egymásra. Be lehet látni, hogy a skalárszorzat rendelkezik egy csomó kellemes tulajdonsággal: pl. kommutatív, disztributív az összeadásra nézve. Ez ad lehetőséget arra, hogy ha két vektor koordinátáival adott, akkor skalárszorzatukat a megfelelő koordinátáik szorzatának az összegeként kiszámolhassuk:

Ugyanis az i, j, k egységvektorokat önmagukkal szorozva 1-et, bármely másikukkal szorozva 0 -t kapunk. A vektorok abszolútértéke az ismert pithagoraszi összefüggésből számítható, így esetünkben a (7, 5, 3) és a (-2, 1, 4) vektorok szöge nem túl sok számolással adódik:

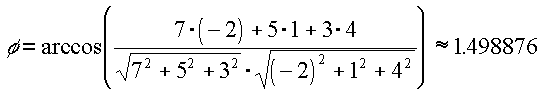
A forgatás megadásához szükségünk lesz még egy vektorra, amely merőleges az előbbi vektorok által meghatározott síkra. Ehhez a vektorok vektoriális szorzatának a fogalmát fogjuk felhasználni. Két vektor - legyenek ezek a és b - vektoriális szorzatán azt az - a x b -vel jelölt vektort értjük, amely

• merőleges a két vektor síkjára;
• nagysága a két vektor hosszának és az általuk bezárt szög szinuszának a szorzata:

.

• iránya olyan, hogy a, b, és a x b ebben a sorrendben u,n. jobb-rendszert alkot. (Erre a feltételre azért van szükség, mert az előző két feltételnek két, egymással ellentétes irányú vektor is megfelelne. Ilyen jobbsodrású rendszert alkot pl. az ábráinkon látható koordinátarendszer X, Y ,Z sorrendben, vagy - innen az elnevezés - a jobb kezünk hüvelyk, mutató és középső ujja ugyancsak ebben a sorrendben, ha a ezeket nyitva, a maradék kettőt csukva igyekszünk tartani.

A vektori szorzat tulajdonságait alaposan elemezve be lehetne látni, hogy miként lehet az a és b - koordinátáival adott - vektor vektori szorzatának a koordinátáit kiszámítani. Aki ismeri a determináns fogalmát, (amely lényegében bizonyos számokból adott szabály szerint képzett szorzat) annak a számára könnyebben megjegyezhető a következő képlet. Ugyanis a vektori szorzat egy olyan determináns első sora szerinti kifejtésével számítható ki, melynek első sorában az  i, j, k egységvektorok, másodikban az a vektor harmadikban a b vektor koordinátái vannak. Persze maga a képlet e fogalom nélkül is megjegyezhető:

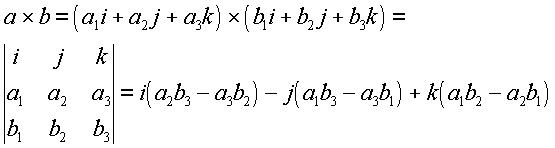
Ezt a képletet a a mi (-2, 1, 4) és a (7, 5, 3) vektorainkra alkalmazva kapjuk a forgatás tengelyének egy pontját:

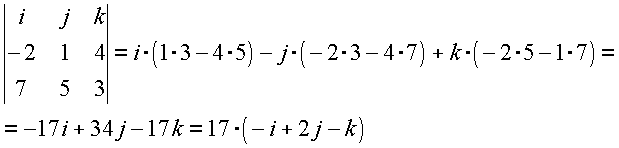
(Azért ebben a sorrendben vettük a vektorokat, mert így a forgatás tengelyén kiválasztott (-1, 2, -1) pontból pozitív irányú forgás viszi a (-2, 1, 4) vektort a (7, 5, 3) -vel megegyező irányba:

Transform { rotation   -1   2   -1    1.498876 } .

Ha mos felveszünk három olyan tetszőleges helyvektort - végpontjaikba egy-egy gömböt helyezve - melyekről tudjuk, hogy egymásra páronként merőlegesek, akkor nem lenne elvi akadálya annak, hogy egy, vagy több forgatással ezeket elmozdítsuk úgy, hogy mindhárom gömb a "világ-" koordinátarendszer egy-egy tengelyére illeszkedjen. p13.wrl , p13a.txt .

(Ha fel szeretnénk venni egy olyan vektort, amely merőleges a (7, 5, 3) vektorra, egyébként tetszőleges, akkor csak arra kell ügyelnünk, hogy elégítse ki a  7x + 5y + 3z = 0  egyenletet. A harmadikat ezekből már a vektori szorzat felhasználásával számíthatjuk ki.)

Ez az egyértelműen meghatározott célú transzformáció (sorozat) azonban már igen sok és kellemetlen számolást igényelne. E feladat megoldására vezette be a VRML alkotógárdája a mátrix transzformációt, amely egyetlen adatstruktúrával megoldja a problémát. Ennek az alkalmazása ugyancsak komolyabb matematikai meggondolásokat igényelne.  Az ezzel kapcsolatos ismereteket ismét átugorhatják  a téma iránt kevésbé érdeklődők, ugyanis a gyakorlatban megkímélhetjük magunkat ezektől a hosszadalmas és koránt sem egyszerű számolásoktól.

A mátrix transzformáció az alábbi matematikai összefüggésen alapszik. Legyen a,  b,  c  három, egymásra páronként merőleges, ebben a sorrendben jobbsodrású vektor. Ha az XYZ térbeli derékszögű koordinátarendszer ugyancsak jobbsodrású, akkor az a,  b,  c  vektorok rendre ráilleszthetők az X, Y, Z  tengelyekre egy térbeli mozgással (iránytartó egybevágósági transzformációval).

Jelölje rendre  az a, b, c vektoroknak az X, Y, Z tengelyekkel bezárt szögeit. Az a kérdés, hogy mik lesznek az (a, b, c) alakzattal együtt mozgó P(x, y, z) pontnak az új P(x' , y' , z' ) koordinátái? (A "mi mozog, mihez képest mozog?" kérdés alapján ugyanez úgy is fogalmazható, hogy mik lesznek a P pont koordinátái az új rendszerben?) A Választ az alábbi transzformációs képlet adja:

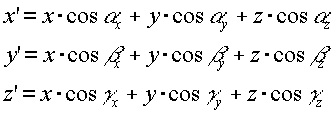
Ebben a képletben az előbbi szögek koszinuszai szerepelnek, amelyeket szerencsénkre könnyebb megadni, mint magukat a szögeket. Ha ugyanis az a, b c vektorok egyaránt egységnyi hosszúak, akkor a vektorok koordinátái éppen a szóban forgó szögek koszinuszai. Ezt pedig könnyen ki lehet számolni, hiszen elegendő minden koordinátát rendre elosztani aa adott vektor hosszával, amit viszont Pithagorasz tételével határozhatunk meg. AVRML -ben használt mátrix transzformáció lényegében ezeket az együtthatókat tartalmazza. A három gömbből álló alakzatunkat, melyet lényegében az   a(7 ,  5 , 3),   b(-2 , 1 , 3) és a  c( 2.4 , -5.4 ,  3.4) vektorhármas határoz meg, a

transzformációval tudtuk átvinni a kívánt helyzerbe: p14.wrl,   p14a.txt . Figyeljük meg, hogy mind az egy sorban, mind az egy oszlopban lévő számok négyzetösszege - a kerekítésekből adődó hibáktól eltekintve - 1 . Ha ez valamilyen téves beírásból adódóan nem teljesül, vagy valahol elvétünk egy előjelet, akkor a program fut ugyan, de többnyire igen vad alakzatot rajzol, amely az eredetinek valamilyen affin képe. Egyébként ebben a mátrixban megadhatjuk az alakzat eltolását is, az új koordinátarendszer origójának a régi rendszer-beli koordinátáit rendre az alsó sorba írva. Sőt megadhatunk egy un. affin transzformációt is, amennyiben egy-egy oszlopot megszorzunk az adott irány nyújtására vonatkozó tényezővel.

Ezeket a számolgatásokat szerencsére nem kell "kézzel" elvégeznünk.

Az itt bemutatott vrml szerkesztőprogram: szdemo.exe koordináta-transzformációval foglalkozó része - melléktermékként - előállítja azt a transzformációs mátrixot, amelyet alkalmazva pl. a fenti mátrixot előállíthatjuk.

Itt jegyezzük meg, hogy ez a vrml szerkesztő program (demo változata) kissé eltér az előzőleg közölt verziótól. Ez a változat már képes olyan VRML 1.0 fájlokat előállítani, amelyek a Cosmo Player megjelenítőn is futtathatók.

Végül, - ha már részben a matematikai ismeretek jegyében telt a kedves olvasónak az e cikk megismerésére fordított ideje - bemutatunk egy - ugyancsak matematikai -példát a VRML transzformációinak egy gyakorlati alkalmazására.

A középiskolai matematika anyag egyik igen érdekes, de sokak számára talán kevéssé szemléletes része az első n természetes szám négyzetösszegére vonatkozó összefüggés igazolása:

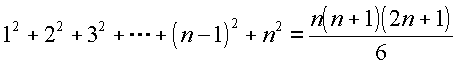
Ha arra nem is vállalkozunk, hogy minden igényt kielégítő bizonyítást adjunk erre az összefüggésre, megkíséreljük kissé szemléletesebbé tenni a problémát.

Elsőként vegyük szemügyre ezt a "tornyot" !

A torony egy egy rétege rendre, 1, 2, 3, . . .7 oldalhosszúságú nényzet alapú hasáb, így 1, 4, 9, .. 49 kockából áll. Ez azt jelenti, hogy maga a torony az első 7 pozitív egész szám négyzetösszgének megfelelő számú kockából áll. Ha hat ilyen tornyot megfelelően - mintegy térbeli puzzle-ként össze tudunk áll1tani egy téglatestté, amelynek élei rendre 7 ,   7+1 , ill 2*7+1, akkor ezzel n=7 -re pontosan beláttuk az összefüggést. Mivel azonban nincs elvi akadálya, hogy tornyunkat tovább növeljük, és  6  ilyen n rétegű toronyból összeállítsunk egy n(n+1)(2n+1) egység-kockányi téglatestet, azt mondhatjuk , hogy a bizonyításunk teljes.

A téglatest összeállíthatóságát ezek a vrml jelenetek mutatják:

2 torony , 3 torony  , 3 együtt ,   6 torony , téglatest.

A legutóbbi jelenet forrásfájljából kiderül, hogy az előző, "szellős" jeleneteket a most kiiktatott eltolásokkal kaptuk.

Végül, engedje meg a kedves érdeklődő, hogy kitűzzünk néhány olyan feladatot, amelyekben az itt megismert összefüggéseket alkalmazva készíthetünk - az előzőek alkalmazásaként - érdekes geometrjuai alakzatokat megjelenítőVRML jeleneteket:

Van egy érdekes geometriai konstrukció, az un. Sierpinski szivacs. Ezt úgy származtathatjuk a kockából, hogy felbontjuk 3*3*3 kisebb kockára. Ezek közül eltávolítjuk az összes olyat, amelynek nincs közös éle az eredeti kockával. A megmaradt kis kockákkal megísmételjük ezt a műveletet. Elvileg végtelen sokszor, ezen a rajzon csak egyszer.

Készítsünk vrml alakzatot erről a matematikai csodabogárról! (Megjegyezzük, hogy elegendő hozzá a Cube{} alakzat, valamint a Translation { translation ? ? ? } művelet.)

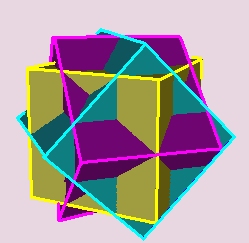
Ez a kép is egy VRML fájl alapján készült. Lényegében egy dolgot kellett megoldanunk: azt, hogy milyen irányú tengely körül, mekkora szöggel kell elforgatnunk a kockát, hogy ezt az alakzatot kapjuk. Mivel senkit nem szeretnénk megfosztani az önálló alkotás örömétől, itt most közöljük a kép elkészítéséhez használt VRML forrásprogramot, csak éppen a lényeget, a forgatások adatait nem adjuk meg.

Ennek a másik alakzatnak az előállításához pontosan ugyanazokat a forgatásokat kell alkalmaznunk. Az ehhez szükséges VRML fájl elkészítését teljes egészében az olvasóra bízzuk. Itt az a fő kérdés, hogy milyen alakzatból (poliéderből) kapjuk a megfelelő forgatásokkal a keresett alakzatot.

A most megismert lehetőségeink birtokában még várhatóan sok ilyen bogarat fogunk gombostű végre venni. Reméljük, a most felvillantott lehetőségek további ötletgazdag VRML konstrukciók megalkotására inspirálják olvasóinkat.

Minden érdeklődőnek az önálló felfedezés örömét, jó munkát kíván: