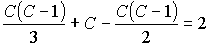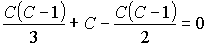A Császár-poliéder
A történet
1949-ben kezdődött.
Ebben az évben
rendezték meg második alkalommal az azóta közismertté vált Kürschák József
matematikai versenyt. A verseny egyik feladata így hangzott:
| Igazoljuk,
hogy egyetlen olyan poliéder létezik, amelynek nincs átlója, (azaz bármely
két csúcsát él köti össze) és ez a tetraéder. |
A feladat kitűzői
feltehetően az alábbihoz hasonló -topológiai bizonyítást várták a verseny
résztvevőitől:
Bármely egyszerű
poliéder lapjai, csúcsai és élei között fennáll az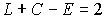 összefüggés, ahol L a lapok C a csúcsok, E az élek
számát jelenti.
összefüggés, ahol L a lapok C a csúcsok, E az élek
számát jelenti.
Legyen a feltételeknek
eleget tevő poliédernek C csúcsa. Mivel bármely két csúcsnak van
közös éle, ezért egy csúcsból C-1 él indul ki, így az élek száma 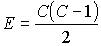 ,
hiszen minden él két csúcshoz tartozik. ,
hiszen minden él két csúcshoz tartozik.
A poliéder
lapjai csak háromszögek lehetnek, hiszen pl. egy négyszögnek már van átlója.
Így - mivel minden csúcsba C-1 háromszög fut be - a lapok száma 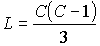 ugyancsak
azért, mert egy lap három csúcshoz tartozik. ugyancsak
azért, mert egy lap három csúcshoz tartozik.
Végül - mivel
a keresett poliéder egyszerű - alkalmazható rá az Euler-tétel. Az L
és E értékét ebbe behelyettesítve C-re egy másodfokú egyenletet
kapunk:
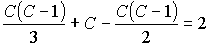
melynek a gyökei
C
= 3 és C =4 .
Ezek közül
- mivel egy poliédernek legalább 4 csúcsa van - csak az utóbbi jelent megoldást,
ez pedig valóban a tetraéder. Megjegyezzük, hogy a C=3-nak is van
geometriai ( topológiai) tartalma. Gondoljunk pl. arra, hogy egy gömb valamely
körén (pl egy főkörén) elhelyezünk három pontot. Ezek -topológiai szempontból
- két háromszöget alkotnak, így adódik az L=2 ,C=3, E=3
megoldás, amelyben a két háromszög mindhárom oldala mentén szomszédos. |
Mint utóbb
kiderült, a feladat a vártnál nehezebbnek bizonyult. Ugyanis a feladat
kikötései között nem szerepelt, hogy az egyszerű
poliéderekre
érvényes állítással van dolguk a versenyzőknek.
A felkészültebb,
körültekintőbb diákok, akik nem szerették volna leszűkíteni a bizonyítást
az egyszerű poliéderek körére, többnyire tudtak arról, hogy az egyszerű
sokszögekkel határolt de topológiai szempontból tóruszt alkotó poliéderekre
az Euler-tétel így módosul:
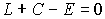
A fenti gondolatmenet
ez esetben is alkalmazható, mindössze egy helyen kell módosítani a meggondolásainkat,
az utóbbi egyenlet jobb oldalára 2 helyett 0 -t kell írnunk:
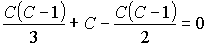
Ebből aC
= 7 értéket kapjuk megoldásként, melyhez
L=14,E=21
érték tartozik.
A kérdés tehát
immár az, hogy:
| Van-e olyan
- topológiailag tórusz-szerű - 7 csúcsú, 14 lapú, 21 élű - poliéder,
amelynek nincs átlója, azaz bármely két csúcsát él köti össze? |
A kérdést Császár Ákos professzornak, aki annak
idején a Budapesti Eötvös Loránd Tudományegyetem Matematikai Intézetének
a tanársegédje volt, nemsokkal a versenyt követően sikerült negválaszolnia,
majd a kapott eredményt közölnie:
CSÁSZÁR Á: A polyhedron without diagonals , Acta Sci Math. 13 (1949-50),
pp 140 - 142
Az ehhez hasonló matematikai eredmények leírása
- a kapott eredmény közlésén túl kiterjed annak a precíz igazolására, hogy
ez a konstrukció valóban létezik, de - a legtöbb esetben - nem tér
ki azokra a részletekre, ötletekre, amelyeket a konstrukció megalkotójának
feltehetően végig kellett járnia.
Ezt a felfedező utat most megkíséreljük rekonstruálni,
felvillantva olyan ötleteket, melyek esetleg másutt is hasznosíthatók lesznek
olvasóink számára. Akik azonban inkább
a végeredményre kíváncsiak, ugorják át ezt a részt.
Először is rajzoljuk meg a tórusz felületére
illeszkedő teljes gráfot. Vajon hányféleképpen tehetjük ezt meg?
Mint már említettük egy tórusz felülete szemléltethető
egy olyan téglalappal, melynek a szemközti oldalélei egybeesnek.
Az egybeeső téglalap-éleket egyszerűbb úgy szemlélnünk, (szemléltetnünk?
) mint ha ezzel a "mintás' téglalappal vagy akár paralelogrammával) parkettáznánk
ki hézagmentesen a síkot.
Nem tartozik a témánkhoz, de ilyen képeket alkalmaznak pl. háttérként
a weblapok készítői, melyekkel kiparkettázva a hátteret, nem lehet
látni, hogy hol a rácsosan elrendezett kép határa.
Egy ilyen téglalap (paralelogramma) helyett
vehetünk egy olyan tetszőleges alakzatot, amely alkalmas arra, hogy pusztán
párhuzamos eltolásokat alkalmazva kiparkettázzuk vele a síkot.
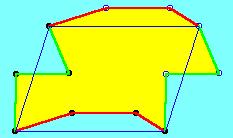
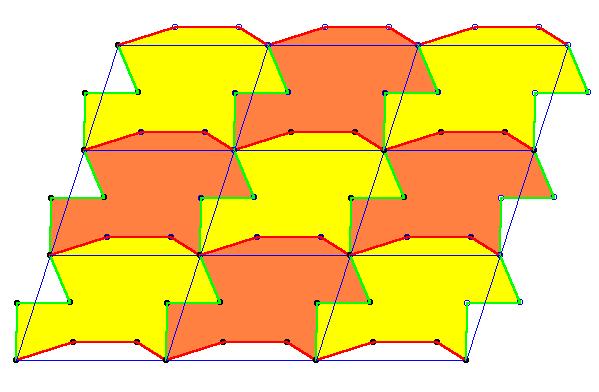
Mivel a keresett poliéder csupán háromszögekből
áll, melynek minden csúcsára 6 háromszög illeszkedik, vegyünk egy (nem
feltétlenül szabályos) háromszögrácsot, számozzuk meg a rácspontokat
alkalmas módon, majd válasszunk ki a síkon egy az előző feltételeknek
megfelelő alakzatot, amely lényegében a tóruszra rajzolt gráf lesz.
A számozást úgy kell elvégeznünk (1és 7 közötti
számokkal), hogy a közös él mindkét végpontjában más-más szám szerepeljen.
Mivel az egész kiparkettázott sík rácspontjait be kell számoznunk,
választhatjuk pl. az egy egyenes menti rácspontok számait rendre 1-től
7-ig. Ez a sorrendet ugyanígy meg kell hagynunk a "felette" ill. "alatta"
lévő sorban, olyan eltolásokkal, hogy pl. a 7. csúcsnak a felette lévő
szomszédjai csak a 2 és 3,vagy a 4 és 5 lehet. (Az
egyik lehetőséget választva valójában nem
kerültünk döntéshelyzetbe, hiszen a két eset egymás tükörképe.)
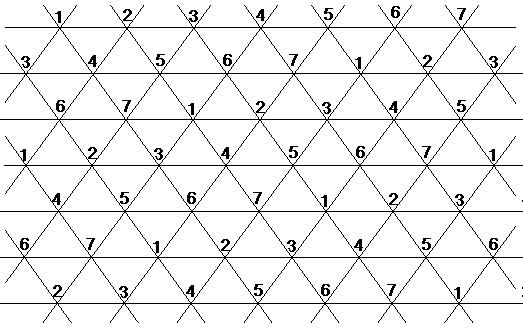
Erről a háromszögrácsról, amelynek az azonos
sorszámú csúcsait azonosaknak tekintjük, máris leolvasható, hogy mely háromszögek
alkotják a tórusz felületét, és az egy csúcsba befutó élek, ill. lapok
milyen sorrendben követik egymást.
A gráf, ill. a keresett poliéder lapjai
- melyeket a csúcsok sorszámaival adunk meg - tehát:
|
[1,2,6]
|
[2,3,5]
|
[3,5,6]
|
[4,6,7]
|
[2,3,7]
|
[2,3,7]
|
[2,6,7]
|
|
[6,5,1]
|
[5,4,2]
|
[4,2,1]
|
[4,3,1]
|
[3,1,7]
|
[5,4,7]
|
[5,1,7]
|
A lapok,
azon belül a csúcsok felsorolását tetszőleges sorrendben megtehetjük, itt
azonban máris érvényesült egy tendencia, már a felsorolásban is érzékeltettük,
hogy az (1-6) , a (2-5) és a (3-4) csúcs-párok a 7. csúcshoz viszonyítva
szimmetrikusan helyezkednek el. Ezt a konstrukcióban is ki fogjuk
használni. Ezért máris úgy választottuk ki a háromszögrácsból a tórusz
felületet alkotó -topológiai értelemben vett - téglalapot, hogy az
élei ne messék a 7. csúcsba befutó éleket.
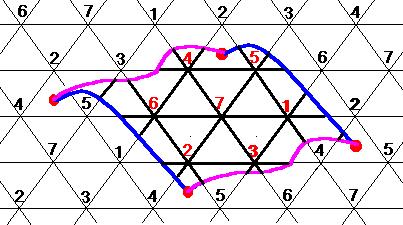
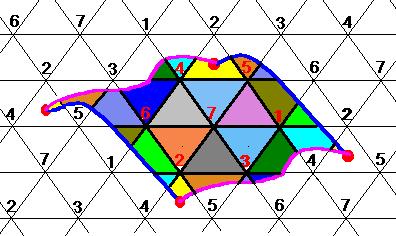
Egy felületre rajzolt gráfot nem elegendő az
éleivel megadnunk, azt is meg kell adnunk hogy a felületet alkotó tartományokat
(lapokat) milyen -topológiai értelemben vett - sokszögek alkotják,
sőt azt is, hogy ezek egy-egy csúcsra milyen sorrendben illeszkednek. Esetünkben
ezekről az ábrákról ez is leolvasható:
|
Csúcs
|
szomszédai rendre:
|
|
1.
|
2, 6, 5, 7, 3, 4
|
|
2.
|
3, 7, 6, 1, 4, 5
|
|
3.
|
4, 1, 7, 2, 5, 6
|
|
4.
|
5, 2, 1, 3, 6, 7
|
|
5.
|
6, 3, 2, 4, 7, 1
|
|
6.
|
7, 4, 3, 5, 1, 2
|
|
7
|
1, 5, 4, 6, 2, 3
|
A fenti két táblázat bármelyike, vagy a gráf -
sorszámozással ellátott - rajza már egyértelműen meghatározza magát
a gráfot. Ez azt jelenti, hogy bármalyik "objektum" ismeretében a
másik kettő meghatározható. Egy felületre - jelen esetben a tóruszra
- rajzolt gráfot, (éppúgy mint egy poliédert) nem határozhatunk meg
egyértelműen azzal, hogy megadjuk az un. koincidencia mátrixát, vagyis
az éleit.
Megállapíthatjuk
tehát, hogy a tóruszra rajzolt 7 csúcsú teljes gráf egyértelműen meghatározott,
vagyis bárhogyan készítjük is el a keresett poliédert, az homeomorf (topológiai
szempontból azonos) lesz az itt leírt gráffal.
Nos, fogjunk
hozzá a poliéder megadásához.
Olyan konstrukciót
fogunk tervezni, hogy az legyen tengelyesen
szimmetrikus. A szimmetriatengelyére illeszkedjen
(pl.) a 7. csúcs, ez esetben az 1 és 6 , a
2 és 5 , valamin a 3 és 4 csúcsok egymás tükörképei lesznek.
Induljunk ki abból, hogy felveszünk az
xy síkban egy az origóra szimmetrikus helyzetű
négyzetet, majd két átellenes csúcsát kissé elmozdítjuk a z
tengely
irányába. Ezzel megadtuk 4 csúcsot, mondjuk az (1
2 6) és (6 5 1) lapokat.
A (2-5) élre illeszkedő két háromszög illeszkedik
még a 3. ill. 4. csúcsra. Ezt a két csúcsot - a szimmetriára
tett ígéretünket betartva - csak úgy vehetjük fel, hogy a 3. csúcs
első két koordinátája teljesüljön, hogy y
>abs(x) , mert ellenkező esetben nem megfelelő sorrendben követnék
egymást a (2 3 5) és (5 4 2) lapok , másrészt teljesülnie kell az
x>0feltételnek
, mert másképp a (2 3 5) és (3,5 6 ) lapok lennének önátmetszők,
harmadrészt nem lehet túl nagy a (3-4) él, mert
belemetszene a később kialakítandó (1 5 7) lapba. Ezt a két csúcsot megadva
poliéderünk már 8 lapból áll, és csak egy csúcsa hiányzik. Már
kialakult a "lyuk" a poliéderen a (2-5) és a (3-4) élek között.
Az eddig kialakított modellünkön látszik,
hogy ha pl. csökkenteni szeretnénk a (3-6) élhez tartozó - konkáv - lapszöget,
akkor a 3. csúcs x
koordinátáját kellene növelnünk, de ettől a (2-5) él ugyancsak konkáv lapszöge
növekedne, vagy növelhetnénk a z
koordinátáját, ettől viszont a 7. csúcsot kellene túl messzire felvennünk.
Igaz, megtehetnénk, hogy az irányokat megtartva a(3-4) él hosszát csökkentjük,
ekkor azonban csak a (2-5) él lapszöge növekedne, és kevéssé csökkenne
a (3-6) él lapszöge.
A 7. csúcsot eléggé távol felvéve a Z
tengelyen, le tudjuk zárni a felületet úgy, hogy egyik háromszöglap se
messe a többit.
Ezzel előállítottuk a poliédert,
mint azt Császár Ákos tette 1949-ben.
A poliédert szemlélve észrevehetjük,
hogy bár tengelyesen szimmetrikus, síkra vonatkozóan nem, tehát létezik
egy "jobbos" és egy "balos" változata, amelyek egymásnak síkra vonatkozó
tükörképei.
A
Császár poliéderek adatai
A már kész konstrukcióval kapcsolatban két
kérdés vethető fel:
| - Meg lehet-e egy picit
változtatni a csúcsok koordinátáit úgy, hogy valamivel "szellősebb"
legyen a poliéder?
- Meg lehet-e alaposan
változtatni a csúcsok koordinátáit úgy, hogy alapvetően más elrendezésű,
de ugyancsak átló nélküli poliédert kapjunk? |
Kérdéseink megválaszolásához meg kell állapodnunk
néhány fogalomban. A "szellősebb" jelző szubjektív, nem mondhatjuk, hogy
ha az egyik konkáv lapszöget csökkentjük, akkor jobb, szellősebb változatot
kapunk, mert lehet, hogy egy másik ugyanekkor nagyobb lesz, vagy egy konvex
még kisebb.
Nevezzük a Császár poliéder két modelljét
alapvetően
azonosnak ha
- az egyik poliéder egy síkra
vonatkozó tükrözéssel átvihető a másikba;
- az egyik poliéder csúcsainak a koordinátáit
folytonosan változtatva átvihető a másikba anélkül, hogy eközben önátmetszővé
válna a felület;
- az egyik poliéder előző két művelet egymás
utáni végrehajtásával vihető át a másikba;
egyébként két Császár poliéder alapvetően
különböző. |
A célunk tehát egyrészt az, hogy az alapvetően
azonos poliéderek között keressünk minél szellősebb, tetszetősebb változatot,
másrészt, hogy keressünk alapvetően különböző változatokat.
1986-ban két német szerző bebizonyította, hogy
a Császár poliédernek négy alapvetően különböző
változata létezik több nincs.
JÜRGEN BOKOWSKI, ANSELM EGGERT:
All realizations of Möbius'torus with 7 vertices preprint Technishe
Hochschule Darmstadt, 1986
Most rendre bemutatjuk e négy változat egy
- egy a lehetőségekhez képest szellősnek tekinthető példányát. A
poliéderek elkészítéséhez rajzokat is mellékelünk. Reméljük, hogy a rajzok,
és a közölt adatok alapján érdeklődőbb olvasóink el is készítik a poliéderek
modelljeit. A
hálózatból attól függően kapjuk
a jobbos, ill. balos változatot, hogy a legelső hajlítást magunk felé,
vagy az ezzel ellentétes irányba végezzük. A
rajzokon a piros él azt jelzi, hogy az ehhez tartozó lapszög konkáv.
A modellek VRML fájljait érdemes megszemlélnünk
"élvázas" formájukban is, így könnyebben észrevehetők az egyes változatok
közötti eltérések, melyek lényegében az (1-6), (2 -5) és (3 -4) él ill.
7. csúcs egymáshoz viszonyított elrendezésében mutatkoznak meg.
Csúcsok:
| |
Eredeti
|
Cs1
|
Cs2
|
Cs3
|
Cs4
|
|
Nr.
|
X
|
y
|
z
|
x
|
y
|
z
|
x
|
y
|
z
|
x
|
y
|
x
|
y
|
z
|
z
|
|
1.
|
3
|
-3
|
0
|
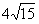
|
0
|
0
|
12
|
0
|
0
|
12
|
0
|
0
|
12
|
0
|
0
|
|
2.
|
3
|
3
|
1
|
0
|
8
|
4
|
0
|
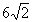
|
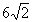
|
0
|
12
|
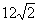
|
0
|
12
|
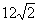
|
|
3.
|
1
|
2
|
3
|
-1
|
2
|
11
|
3
|
-3
|
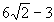
|
-4
|
-3
|
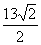
|
-3
|
3
|
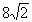
|
|
4.
|
-1
|
-2
|
3
|
1
|
-2
|
11
|
-3
|
3
|
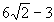
|
4
|
3
|
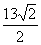
|
3
|
-3
|
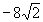
|
|
5.
|
3
|
3
|
-1
|
0
|
-8
|
4
|
0
|
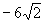
|
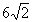
|
0
|
-12
|
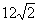
|
0
|
-12
|
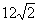
|
|
6.
|
-3
|
0
|
3
|
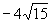
|
0
|
0
|
-12
|
0
|
0
|
-12
|
0
|
0
|
-12
|
0
|
0
|
|
7.
|
0
|
0
|
15
|
0
|
20
|
0
|
0
|
0
|
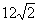
|
0
|
0
|
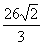
|
0
|
0
|
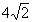
|
|
Élek
|
Eredeti
|
Cs1
|
Cs2
|
Cs3
|
Cs4
|
|
d
|
f
|
d
|
f
|
d
|
f
|
d
|
f
|
d
|
f
|
|
(1-6)
|
8.5 |
153° |
31.0 |
127° |
24 |
90° |
24 |
71° |
24 |
22° |
|
(2-5)
|
8.5 |
321° |
16.0 |
344° |
16.9 |
270° |
24 |
204° |
24 |
56° |
|
(3-4)
|
4.5 |
253° |
4.5 |
257° |
8.5 |
114° |
10 |
76° |
8.5 |
286° |
|
(2-4)=(5-3)
|
6.7 |
78° |
12.3 |
69° |
6.9 |
296° |
12.6 |
204° |
16.3 |
191° |
|
(2-3)=(5-4)
|
3 |
216° |
9.3 |
209° |
12.2 |
35° |
17.4 |
42° |
11.0 |
103° |
|
(3-7)=(4-7)
|
12.2 |
269° |
9.3 |
279° |
12.2 |
291° |
5.9 |
244° |
7.1 |
22° |
|
((2-7)=(5-7)
|
14.6 |
18° |
17.9 |
36° |
12 |
61° |
12.9 |
340° |
16.5 |
307° |
|
(1-5)=(6-2)
|
6.1 |
87° |
17.9 |
90° |
16.9 |
90° |
24 |
53° |
24 |
39° |
|
(1-2)=(6-5)
|
6.1 |
44° |
17.9 |
67° |
16.9 |
15° |
24 |
53° |
24 |
66° |
|
(1-4)=(6-3)
|
5.1 |
352° |
18.3 |
343° |
16.2 |
237° |
12.6 |
157° |
14.8 |
39° |
|
(1-3)=(6-4)
|
6.2 |
58° |
19.9 |
57° |
11.0 |
279° |
18.7 |
339° |
19.0 |
272° |
|
(1-7)=(6-7)
|
15.3 |
76° |
25.3 |
57° |
20.8 |
24° |
17.1 |
74° |
13.3 |
272° |
d : Az élek hossza;
f: Az élekhez tartozó lapok szöge.
Cs0Az
eredeti változat. Ezehket a koordinátákat közölte Császár Ákos 1949-ben.
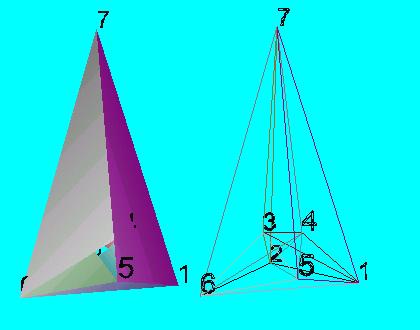
Cs1ax.wrl
Cs1thin.wrl
Sorrend a z
tengelyen
(1-6) , (2-5) , (3-4) , 7 Alapvetően azonos Cs0-al.
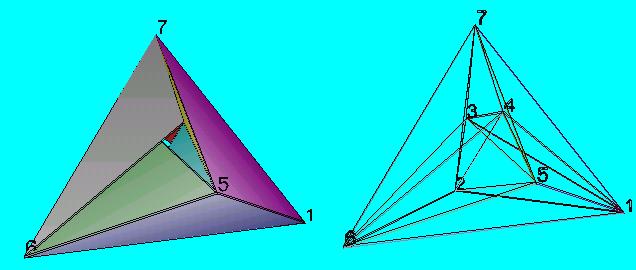
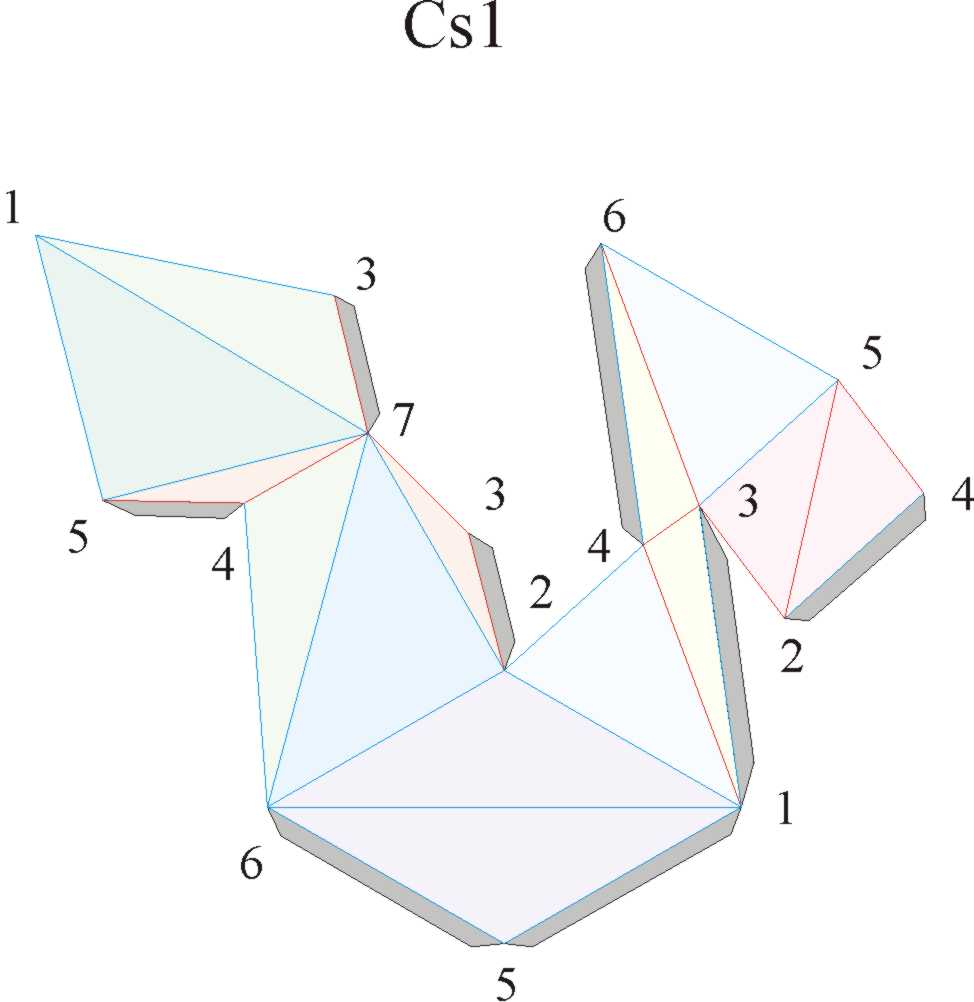
A lapok összeragasztásának javasolt sorrendje:
-
2 - 4 él;
-
2 - 3 él;
-
6 - 4 él;
-
4 - 5 él;
-
5 - 1 , 1
- 3 és 3
-7 él mentén.
Cs2ax.wrl
Cs2thin.wrl
Sorrend a z
tengelyen
(1-6) , (3-4) , (2-5) , 7
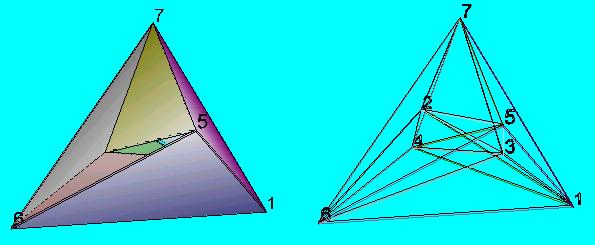
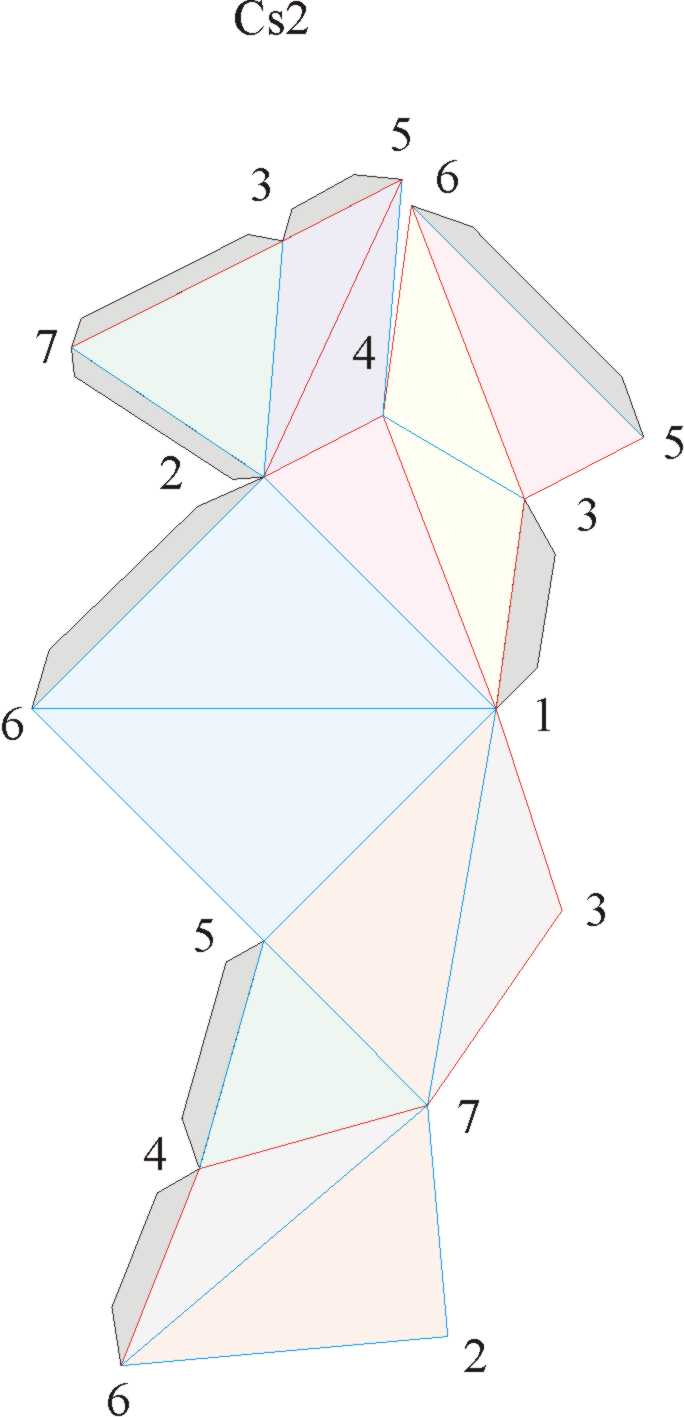
A lapok összeragasztásának javasolt sorrendje:
-
3 - 5 él;
-
1 - 3 és
3 - 7 él;
-
6 - 5 él;
-
5 - 4 és 4
- 6 él;
-
7 - 2 és 2
- 6 él mentén.
Cs3ax.wrlCs3thin.wrl
Sorrend a z
tengelyen
(1-6) , (3-4) , 7 , (2-5)
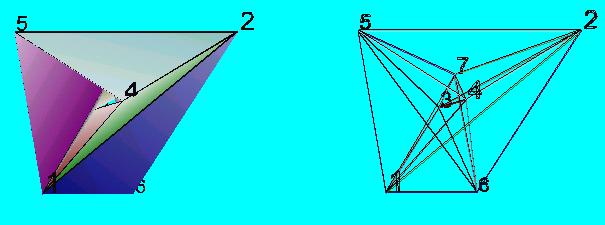
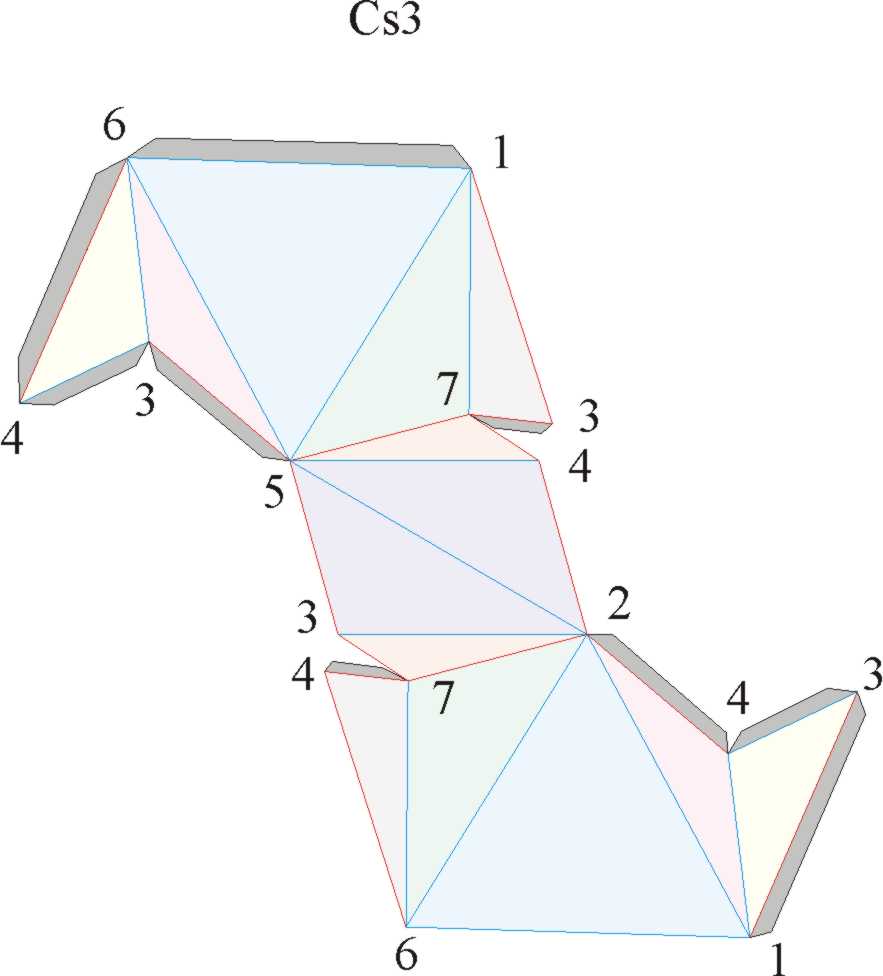
A lapok összeragasztásának javasolt sorrendje:
-
4 - 7 és
7 - 3 él;
-
3 - 4 él;
-
2 - 4 él;
-
3 - 5 és 3
- 1 él;
-
4 - 6 és
6 - 1 él mentén.
Cs4ax.wrl
Cs4thin.wrl
Sorrend a z
tengelyen
(1-6) , 7 , (3-4) , (2-5)
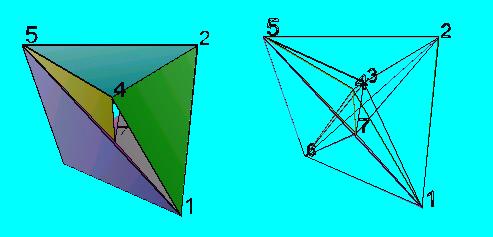
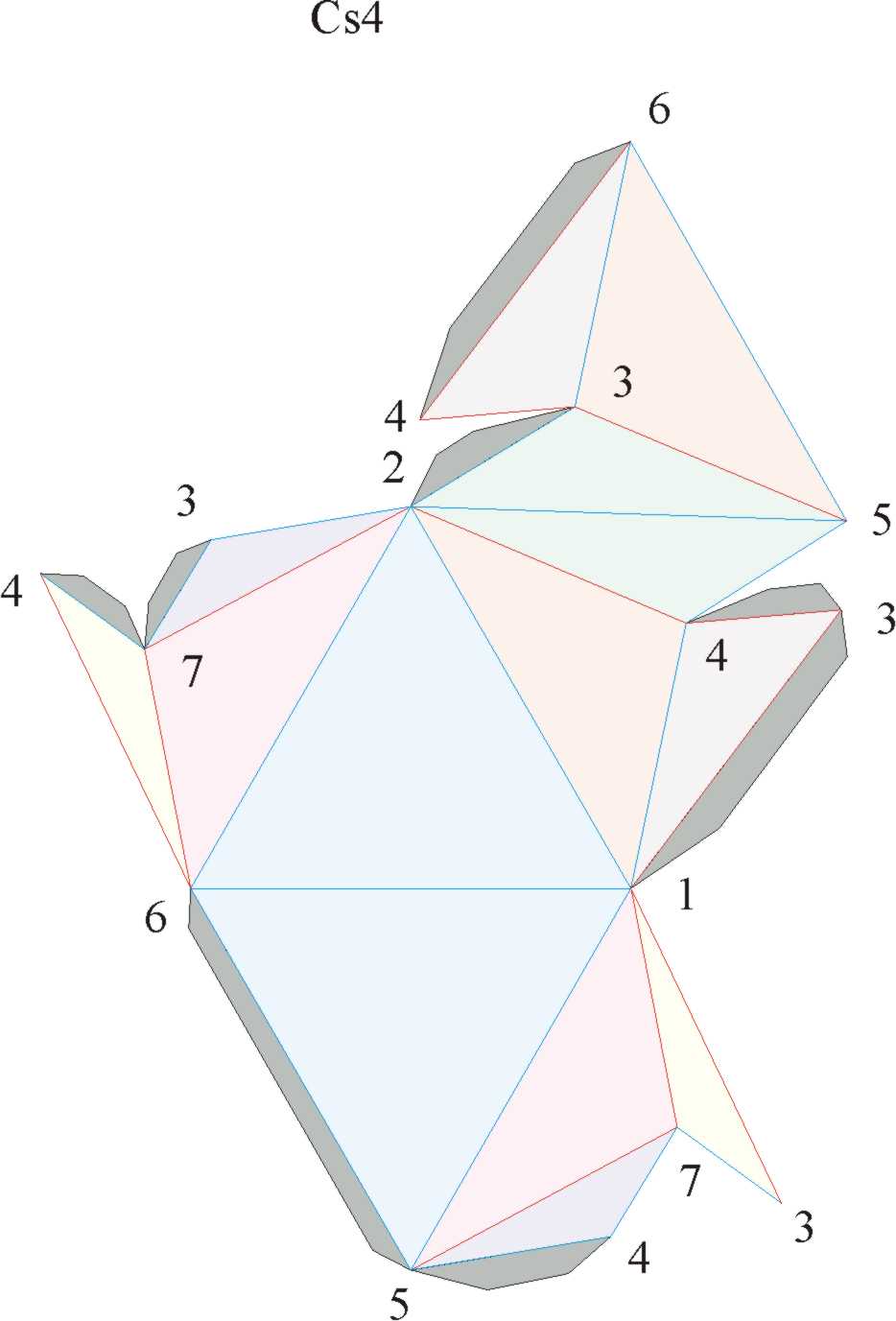
A lapok összeragasztásának javasolt sorrendje:
-
7 - 3 és
7 - 4 él;
-
1 - 3 él;
-
2 - 3 és
3 - 4 él;
-
4 - 6 él;
-
4 - 5 él;
-
5 - 6 él mentén.
A fenti rajzokat
eredetileg a Corel Draw 9.0 változatával készítette egy 2000-ben végzett
hallgatónk: Lédeczi Gyöngyvér. A CorelDraw forrásfájl alapján - amennyiben
ehhez adottak a technikai feltételek - kinyomtatható a poliéder hálózata
az elkészítéséhez megfelelő méretben. A
Corel Draw forrásfájlok rendre:
Cs1.cdr
, Cs2.cdr , Cs3.cdr
, Cs4cdr
Azok számára,
akik tudják használni a MAPLE computeralgebrai programot, átnyújtjuk azt
a forrásfájlt,
amely alapján az itt bemutatott modellek adatait kiszámoltuk, és amelyekkel
újabb, alkalmasint szellősebb elrendezéseket is kereshetünk.
Ez a program ellenőrzi azt is, hogy a megadott koordinátákkal meghatározott
felület nem
önátmetsző-e. Bemutatjuk egyszerűbb példákon azt az eszköztárat
is, amelyekkel ezeket a vizsgálatokat végeztük.Ezeket
a fájlokat megfelelő - elsősorban a számolások matematikai hátterét
megvilágító - magyarázatokkal is elláttuk, így a felvetődő matematikai
problémák iránt érdeklődő olvasóink számára szolgálnak némi tanulsággal.
Szilassi Lajos
Vissza: A poliéderekről
szóló címlapunkhoz.