Addig, amíg egyszerû poliéderek körében  könnyen meghatározható a szabályos poliéderek száma (5, ill. az önátmetszõket is beleértve 9), végtelen sok szabályos toroid  létezik. Mint láttuk, a toroidok körében csak topológiai tulajdonság  a "szabályos" jelzõ.
Gondoljunk csak arra, miként lehetne - folytonos deformálással és amegfelelõ élek összeragasztásával  tóruszt készíteni egy téglalapból. Ragasszuk össze egy téglalap két szemközti élét, ezzel a téglalpból egy henger-palástot kapunk. Ezután  ragasszuk össze a henger két végét, amely eredetileg a téglalap másik két szemközti éle volt. Ezzel elkészítettük a tóruszt.

Azt mondhatjuk tehát, hogy a tórusz topológiai szempontból egy olyan téglalalp, amelynek a szemközti élei egybeesnek, így a téglalap négy csúcsa a tóruszfelület egyetlen pontja lesz..

Mithogy a sík a szabályos sokszögek közül a háromszöggel, négyzettel és a szabályos hatszöggel  - és csak ezekkel - parkettázható ki, ennek megfelelõen  három típusú szabályos toroid létezik:

• T(3,6):  lapjai háromszögek,  minden csúcsába  hat darab háromszög, így hat él fut be;
• T(4,4):  lapjai négyszögek, minden csúcsára négy lap ill. él illeszkedik;
• T(6,3):  lapjai hatszögek, minden csúcsra három  darab hatszöglap ill. három él illeszkedik.

Legkönnyebb négyszöglapú toroidokat elõállítanunk. A  4-4.mws  MAPLE programfájl ilyen toroidokat állít elõ. Nevezzük az így kapott toroid egy sorának azokat az egymáshoz éllel kapcsolódó négyszögeket, melyek a tórusz  - forgástengelyére merõleges -  forgásiránya mentén kapcsolódnak egymáshoz, egy oszlopának a forgásirányra merõlegesen egymáshoz kapcsolódó lapjait.

Ezzel a programmal elõállíthatunk minden olyan toroidot, melynek egy sorában és oszlopában legalább három négyszög van. Így egy ilyen toridnak legalább 3*3=9 lapja van: 44T3_3A.wrl , 44T3_3B.wrl. Tizenkét lapú toroidot kétféle elrendezésben  is elõállíthatunk: 44T4_3.wrl  és 44T3_4.wrl. Ha - mint hamarosan látni fogjuk, nem kizárólag a látvány kedvéért - olyan konstrukciót  tervezünk, amelyen sakktábbla szerûen csak minden második négyszög látható, akkor mind az egy sorban, mind az egy oszlopban lévõ négyszögek számának páros számnak kell lennie. Pl. 44T10_6.wrl.

Felvethetõ a kérdés, hogy lehet-e olyan  N  lapú T(4,4) tipusú szabályos toroidot elõállítani, ahol N nem bontható két olyan szám szorzatára, ahol mindkét tényezõ legalább  3?  Pl. létezik-e 10, vagy 11 lapú T(4,4) típusú toroid?
E sorok írója erre a kérdésre nem tudja a választ. Az biztos, hogy a tóruszra rajzolható ilyen szabályos gráf,  de a kérdés arra vonatkozik, hogy csupán síkbeli négyszögekbõl elõállítható e ilyen toroid. Örömmel vennénk, ha olvasóink közöt alkadna, aki meg tudná válaszolni ezt a kérdést.

A  háromszöglapokból álló T(3,6) típusú toroidok gráfját egyszerûen a négyszögek egyik átlójának a berajzolásával kapjuk a T(4,4) típusból:  36T5_3a.wrl  Ebbõl úgy kaphatunk "igazi" T(3,6) típusú toroidokat (melyeknek a szomszédos lapjai nem esnek egy síkba), hogy vagy minden második sorba, vagy minden második oszlopba esõ csúcspontokat elmozdítjuk fél beosztásnyival. 36T7_3b.wrl    ,   36T7_3c.wrl .

Ezek a vrml fájlok a T(3,6) típusú toroidok elõállítására alkalmas, 3-6.mws MAPLE programmal készültek.

Ebben a programban ugyancsak tetszõlegesen megadható az egy sorban, ill. oszlopban lévõ háromszögek száma. A kínálkozó lehetõségek közül érdemes megemlíteni azt az esetet, amelyben egy sorban 14, egy oszlopban 10 háromszög található. Ekkor ugyanis kiszínezhetõk a háromszögek hét színnel úgy, hogy minden azonos színû (20 háromszögbõl álló) tartomány szomszédos, egyszersmind egybevágó legyen az összes többivel. Ez pedig egy igen szép illusztrációja az un. Heawood- tételnek, miszerint a tóruszra rajzolt bármely térkép kiszínezéséhez elegendõ legfeljebb hét szín. (Egy térképet akkor tekintünk helyesen szinezettnek, ha a szomszédos - aza közös határvonallal rendelkezõ - tartományok különbözó színûek.)

Azt gondoljuk, hogy olvasóink számára ismert ennek a tételnek a sokkal egyszerûbb felületre, a gömbre -vagy ezzel egyenértékû módon a síkra -  megfogalmazott megfelelõje,  az un. négyszíntétel : Igaz- e hogy a síkra rajzolt bármely térkép kiszínezéséhez elegendõ négy szín? A kérdésnek nagy irodalma, az állításnak -miszerint elegendõ a négy szín - számítógéppel végzett  bizonyítása van, de  pusztán matematikai módszereket használó "tiszta" megoldása egyelõre nincs.

Visszatérve a tóruszra:  Heawood azt is megmutatta, hogy a hét szín szükséges is, ugyanis rajzolt a tóruszra olyan  hét tartományból álló térképet, amelyen  bármely két tartomány szomszédos volt, azaz közös határvonallal rendelkezett. Az itt bemutatott tóruszra rajzolt térkép közül bármely kettõ szomszédos (és egybevágó).

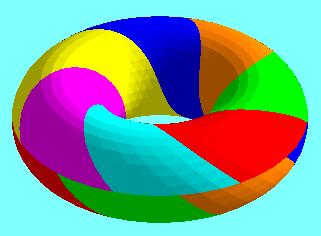
Ilyen Heawood-térkép rajzolható "durvább", Heawood1.wrl, vagy kissé "finomabb" változatban is: Heawood2.wrl, sõt kaphatunk hét egybevágó és páronként szomszédos tartományból álló toroidot mindössze 14 csúcspont felhasználásával is: 7szin4lap.wrl .  Itt egy tartomány négy háromszögbõl áll.: 1szin4lap.wrl (Ez utóbbi két  fájl azonban nem ezzel a Maple programmal készült.)

A  T(6,3) típusú toroidok elõállítása az eddigieknél több számolást igényel, ugyanis gondoskodni kell arról, hogy az egy lapra illeszkedõ hat csúcs egy síkra illeszkedjen, amellett a keletkezõ hatszög ne legyen önátmetszõ. Ezt a változtatható alpszámú toroidot elõállító 6-3.mws  MAPLE programban úgy oldottuk meg, hogy vettünk egy olyan T(4,4) típusú toroidot, amelynek kiválasztható minden második négyszöge, mint pl.  44T10_6.wrl.  Ezzel a négyszögeket lényegében két osztályba soroltuk. Az egyik osztályba tartozó négyzetlapok síkjai lettek a hatszöglapok síkjai. A hatszögek csúcsainak a kiszámításához fel kellett írnunk e síkok egyenletét, majd ebbõl alkalmas  módon hármat-hármat összeválogatva kaptuk azt az egyenletrendszert, amelyet megoldva megkaptuk a hatszög egy csúcsának a koordinátáit. Így állt elõ pl. a 63T5_3.wrl és a 63T7_3.wrl T(6,3) típusú  hatszögekbõl álló toroid. Ez utóbbi egyben  hatszögekbõl állítja elõ a már látott  egybevágó tartományokból álló Heawood-féle térképet.

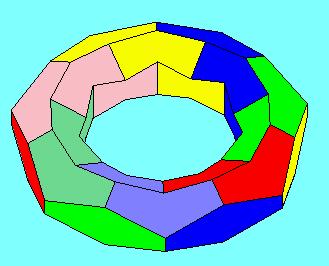
Ezen a rajzon kissé könnyebben megfigyelhetõ, hogy egy adott szín (pl. a piros) az összes többivel szomszédos.

Bemutatunk még egy T(6,3) típusú  toroidot, amely lényegében egy kockából kivágott háromélû prizma: 63Tkocka.wrl.  Az alakzat érdekessége, hogy a ezt a toroidot az egybevágóság szempontjából mindössze kétféle hatszög határolja.

Ugyancsak érdekes a 12, ill. 24 darab L alakú hatszögbõl álló 12L.wrl  és a kissé bonyaolultabb 24L.wrl alakzat, amlyek szintén T(6,3) típusú  toroidok.
(Azutóbbi három vrml  fájl természetesen  nem a 6-3.mws MAPLE program felhasználásával készült, könnyen módositható az itt bemutatott szerkesztõ programmal.)

A bemutatott példák mindegyikében  volt konkáv hatszög is a toroid lapjai között, talán nem véletlenül. Ez alapján megfogalmazható egy sejtés: Nem lehet csupa konvex hatszögbõl T(6,3) típusú szabályos toroidot készíteni. Ugyancsak szívesen vennénk, ha olvasóink között akadna, aki igazolná, vagy cáfolná ezt a sejtést.

Mint láttuk, a szabályos toroidok lapjainak a száma korlátlanul növelhetõ mindhárom típusnál. Felvetõdhet azonban az a kérdés, hogy: Legkevesebb hány sokszögbõl állíthatunk elõ egyik, vagy másik típushoz tartozó szabályos toroidot?

A választ itt találjuk:

• A Császár-poliéderek
• A Szilassi-poliéder