Binomiális eloszlás

Végezzünk független kisérletet egy  esemény bekövetkezésének megfigyelésére.  Legyen  bekövetkezési valószínűsége minden kisérlet esetén   Legyen  valószínűségi változó értéke  bekövetkezéseinek száma.

Ekkor  lehetséges értékei nyilván  lehetnek.

Legyen jelölésben .

Egy ilyen kisérlet során nyilván  vagy  következik be.

Vizsgáljunk az  független kisérlet során egy olyan  hosszúságú sorozatot melyben  esetben következett be  és  esetben következett be .

Az ilyen sorozatok száma kombinatorikai megfontolások alapján .

Mivel feltettük hogy a kisérletek egymástól függetlenek egy ilyen sorozat valószínűségét az egyes kisérletekben bekövetkező események valószínűségeinek szorzatából kapjuk, azaz az eredmény

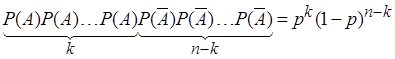
Így annak valószínűsége hogy  pontosan -szor következik be

Egy ilyen valószínűségi változót binomiális eloszlásúnak nevezünk.

A binomiális eloszlás esetén mind a számításokban mind az eloszlás ábrázolásában segítségül hívhatjuk az Excelt.

Egy rögzített paraméterekkel megadott binomiális eloszlás értékeinek kiszámítása a Statisztikai függvények között található BINOM.ELOSZL  függvény segítségével történik.

Ennek fügvénynek mind a négy paraméterét kötelező megadni. A paraméterek jelentése:

Sikeresek paraméter a binomiális eloszlás  paramétere vagyis a megfigyelt kisérlet bekövetkezéseinek száma.

Kisérletek paraméter a binomiális eloszlás  paramétere vagyis a független kisérletek száma.

Siker_valószínűsége paraméter a binomiális eloszlás paramétere, a megfigyelt esemény bekövetkezési valószínűsége.

Eloszlásfv paraméterrel azt állíthatjuk be, hogy a binomiális eloszlás eloszlásfüggvényének vagy sűrűségfüggvényének értékét számítjuk ki.

Az eloszlás ábrázolásához használhatjuk az Excel előbb említett függvényét:

A függvényt ekkor az ábrán látható paraméterezéssel írtuk fel.

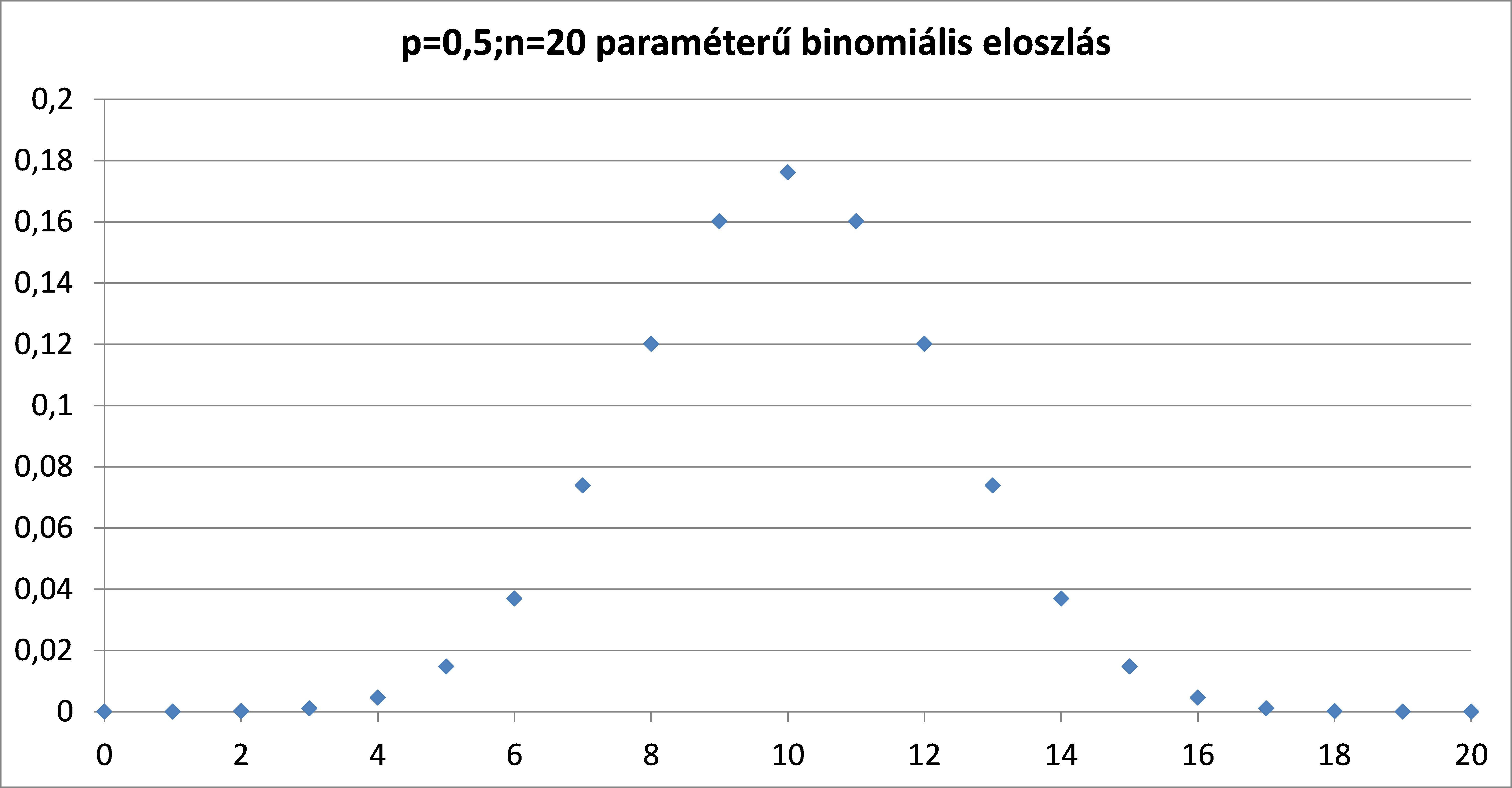
A binomiális eloszlás esetén egy adott (x,y) koordinátájú pont a diszkrét görbén a  pont.

Sok olyan feladat van, ahol  annak valószínűségét kell meghatározni hogy egy binomiális eloszlású változó értéke  intervallumra esik.

Ekkor az a kérdés, hogy mekkora az alábbi valószínűség:

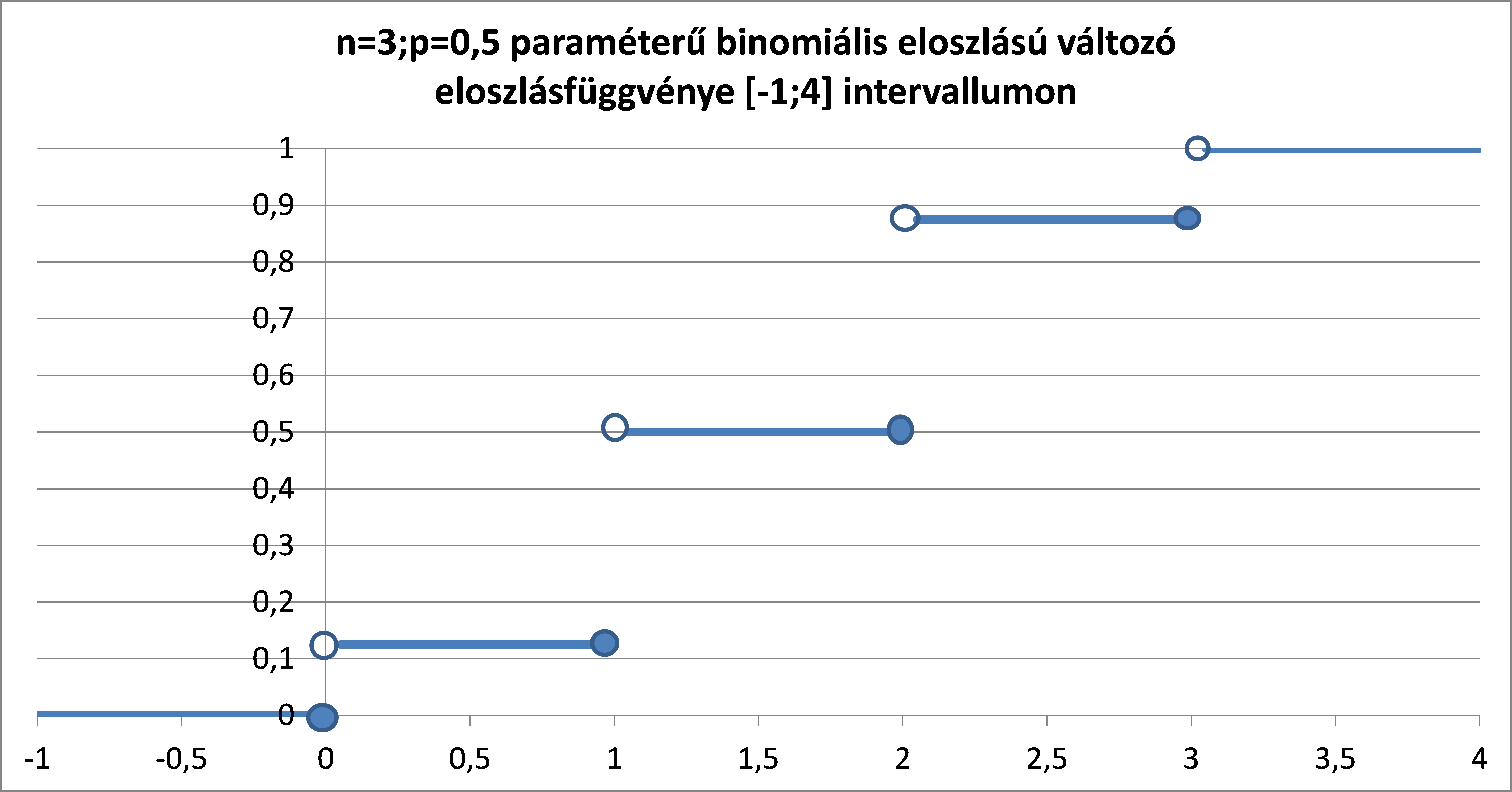
Ha ekkor  akkor arra a kérdésre ad választ az így megszerkesztett kumulált eloszlásgörbe egy pontját az alábbi módon  írhatjuk fel: 

Ennek a pontnak az értelmezése az, hogy mi a valószínűsége annak hogy a változó értéke legfeljebb . Az így kapott diszkrét függvényt láthatjuk  az alábbi ábrán.

Ebből könnyen megszerkeszthető  a binomiális eloszlás eloszlásfüggvénye.

Ahogyan az eloszlásfüggvényeknél is említettük diszkrét eloszlás eloszlásfüggvénye lépcsős függvény, melynek egy adott pontban akkora ugrása van amekkora az adott pont felvételének valószínűsége.

A binomiális eloszlású változó várható értéke: 

Ez a várható érték definíciójából adódik, a következő formula matematikai rendezéséből:

Ezt rendezve és a binomiális tételt kihasználva kapjuk az eredményt.

Szórása a várható értékhez hasonlóan a szórás definíciójából adódik:

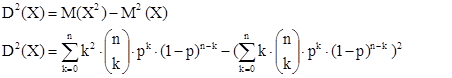
Ennek rendezéséből kapjuk a  formulát.