Sűrűségfüggvény
Definíció. Ha az ![]() valószínűségi változó
valószínűségi változó ![]() eloszlásfüggvénye folytonos, és véges számú pont kivételével a függvény deriválható akkor az
eloszlásfüggvénye folytonos, és véges számú pont kivételével a függvény deriválható akkor az ![]() deriváltfüggvényt az
deriváltfüggvényt az ![]() változó sűrűségfüggvényének nevezzük és
változó sűrűségfüggvényének nevezzük és ![]() -szel jelöljük.
-szel jelöljük.
Ekkor tehát ![]() azaz
azaz ![]() az
az ![]() deriváltfügvénye.
deriváltfügvénye.
Ekkor az előzővel ekvivalens állítást fogalmazunk meg ![]() fentebb említett tulajdonságai alapján:
fentebb említett tulajdonságai alapján:
Ha létezik egy olyan ![]() melyre
melyre
![]()
akkor ![]() függvényt az
függvényt az ![]() változó sűrűségfüggvényének nevezzük.
változó sűrűségfüggvényének nevezzük.
Ekkor ![]() a
a ![]() integrálfüggvénye.
integrálfüggvénye.
A sűrűségfüggvény tulajdonságai:
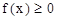 az sűrűségfüggvény nemnegatív
az sűrűségfüggvény nemnegatív-
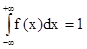
- azaz a sűrűségfüggvény integrálja 1.
A Newton-Leibnitz szabály miatt :
![]()
Ha egy függvény rendelkezik az első két tulajdonsággal akkor egy folytonos valószínűségi változó sűrűségfüggvénye.
Ez azt jelenti hogy a ![]() valószínűséget a sűrűségfüggvény függvény alatti területtel méri az eloszlásfüggvény pedig függvényértékek közötti különbséggel.
valószínűséget a sűrűségfüggvény függvény alatti területtel méri az eloszlásfüggvény pedig függvényértékek közötti különbséggel.