Események függetlensége, Teljes valószínűség, Bayes tétel; független események
Definíció: Egy 
és 
eseményt akkor tekintünk sztochasztikus értelemben függetlennek , ha az egyik esemény bekövetkezése - a feltételes valószínűséggel az alábbi módon megfogalmazott értelemben - nem függ a másik bekövetkezésétől, azaz :
Ekkor a feltételes valószínűség definíciójából könnyen látható hogy:
,
mivel szimmetrikus reláció a két esemény között így könnyen belátható hogy ekkor:
.
Felmerül annak kérdése hogy ez hogyan definiálható több eseményre:
Definíció: Azt mondjuk, hogy , , 
események teljesen függetlenek
- páronként függetlenek,
- mindegyik esemény független a másik kettő szorzateseményétől.
Vagyis ha teljesülnek a következők:
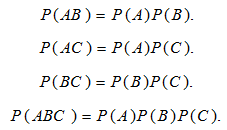
Ehhez hasonlóan tetszőleges véges sok eseményre:
Definíció: 
események teljesen függetlenek, ha bármely 
esetére igaz:
az {
} halmaz tetszőleges 
-elemű részhalmazára.
Teljes valószínűség tétele:
Ahhoz hogy a tételt megfogalmazzuk először definiáljuk a teljes eseményrendszer fogalmát.
Definíció: események teljes eseményrendszert alkotnak, ha páronként kizáróak és összegük a biztos esemény, azaz:
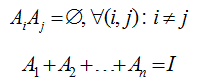
A teljes valószínűség tétele: Legyen teljes eseményrendszer egy eseménytérben.
Legyen ugyanazon eseménytér egy tetszőleges eseménye.
Akkor:
