Kétmintás t-próba azonos szórás esetén
A kétmintás t-próbáknak több változata van. Normális eloszlású változókból indulunk ki és vizsgáljuk először azt az esetet, amikor azt tesszük fel, hogy azonos szórású változóink vannak. Ezen feltétel mellett ellenőrizzük, hogy a várható értékek azonosak-e?
Legyen: 
és 
, és legyenek:
az 
változóhoz tartozó minták 
az 
változóhoz tartozó minták 
.
A nullhipotézis: 
Az alternatív vagy ellen hipotézis pedig: 
.
Jelölje 
az minta szórását,
pedig az minta szórását.
Vegyük a következő statisztikát:
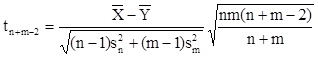
Ha nullhipotézis igaz, akkor ez a statisztika n+m-2 szabadságfokú t-eloszlású.
Ha 
olyan, hogy 
akkor ha a mintából számított 
értékét
jelöli, ha
akkor a nullhipotézist elfogadjuk, a mintából számított statisztika érték a 
elfogadási tartományba esik.
Ha 
akkor a mintából számított statisztika érték a kritikus tartományba esik így a nullhipotézist elvetjük, az alternatív hipotézist fogadjuk el.
Tegyük fel hogy két osztály tanulóinál diszkoszvetés teljesítményt mérünk.
Azt tudjuk hogy a tanulók időteljesítménye normális eloszlású változó azonos szórással.
Az osztályok tanulóinak mintái:
A nullhipotézis:
Az alternatív vagy ellen hipotézis pedig: .
A megengedett elsőfajú hibavalószínűség: 
A statisztika a következő:
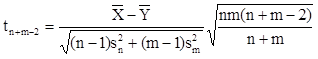
Ezekkel az értékekkel számolva:
Mivel az alternatív hipotézis kétoldali így kétoldali kritikus értékeket határozunk meg.
Ez azt jelenti hogy a mintából mért érték az elfogadási tartományon belül van.
Most döntsünk a próba szignifikanciaszintje, alapján.
A szignifikanciaszint kétoldali alternatív hipotézis esetén a
valószínűségérték.
Kihasználva az eloszlásfüggvény szimmetriájából levezethető
tulajdonságot, kapjuk hogy a szignifikanciaszint ebben az esetben:
.
Mivel ez a szignifikanciaszint nagyobb mint az elsőfajú megengedett hibavalószínűség így a nullhipotézist elfogadjuk.
Ez azt jelenti hogy a mintából mért érték az elfogadási tartományon belül van.
Ezt a szignifikanciaszintet közvetlenül is megkaphatjuk Excelben.
A T.PRÓB függvénynek négy argumentuma van:
- az első paraméter egy tömb, az első minta
- a második paraméter egy tömb a második minta
- a harmadik paraméter annak jelzése hogy:
- egyoldali alternatív hipotézisünk van, ekkor a harmadik paraméter értéke 1
vagy
- kétoldali alternatív hipotézisünk van ekkor a harmadik paraméter értéke 2
- a próba jellemzésére használjuk a negyedik paramétert:
- 1 kétmintás próba párosított
- 2 kétmintás próba egyenlő szórás esetén
- 3 kétmintás próba nem egyenlő szórás esetén
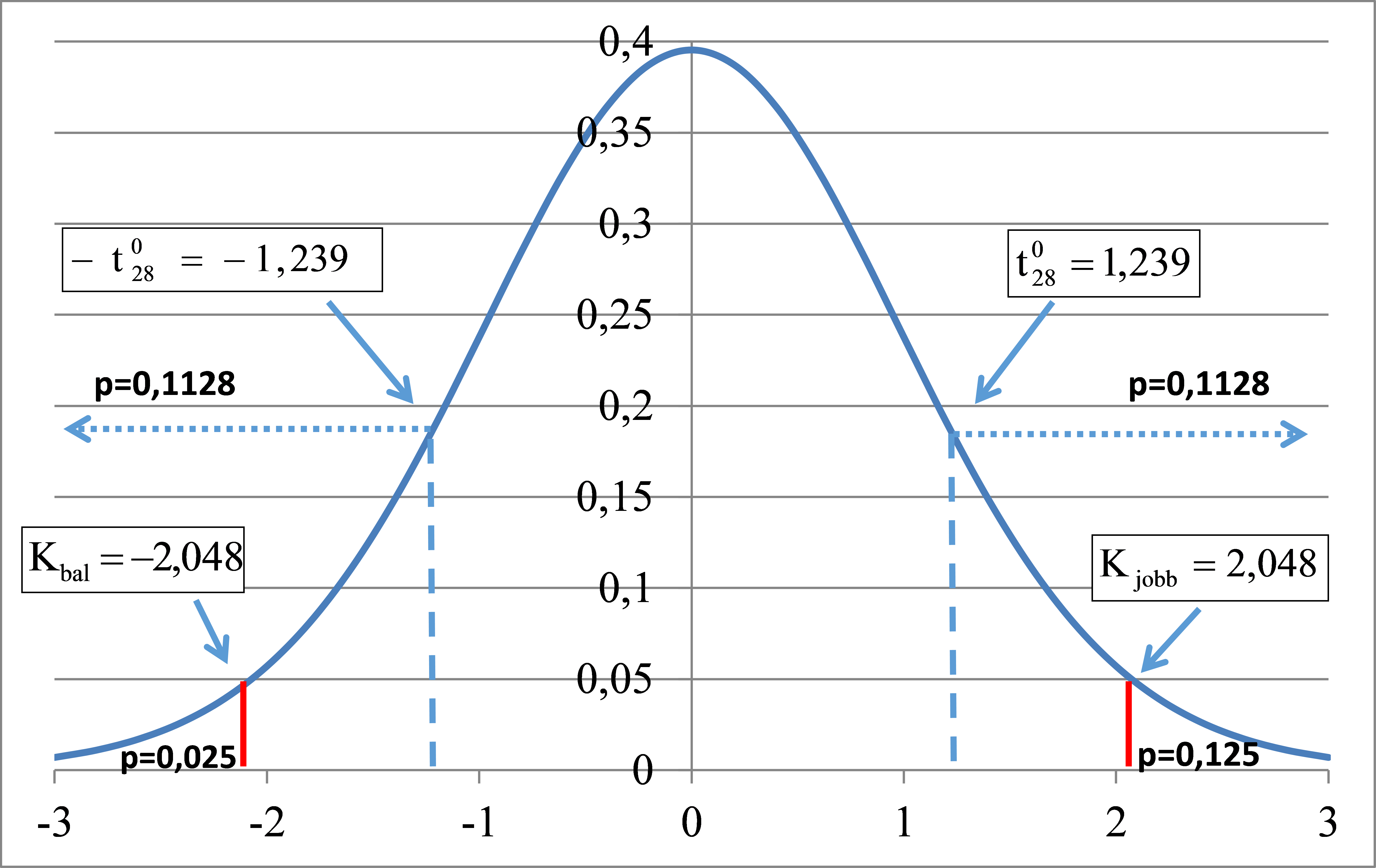
Szemléltetve a szignifikanciaszint alapján történő döntést kétoldali alternatív hipotézis esetén a sűrűségfüggvényen:
