Kétmintás u-próba
Legyen: 
és 
, és legyenek:
az 
változóhoz tartozó minták 
az 
változóhoz tartozó minták 
.
A várható értékre végzünk hipotézisvizsgálatot.
A nullhipotézis:
Az alternatív vagy ellen hipotézis:
Vagyis kétoldali alternatív hipotézisünk van.
A próbastatisztika a következő:
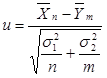
ahol 
.
Ekkor a kétmintás u-statisztika kritikus értékeinek számítása megadható:
innen
Ekkor az elfogadási tartomány a
intervallum, így ha a mintából számított statisztika érték ebbe az intervallumba esik a nullhipotézist elfogadjuk a két változó várható értéke egyenlő.
Ha ezen kívül esik a számított t-statisztika akkor az alternatív hipotézist fogadjuk el, vagyis a várható értékek szignifikánsan különböznek.
Egy példán mutatjuk be ezt a próbát.
Vegyünk két csoportot akik diszkoszvetésben versenyeznek.
Mindkét csoport dobásai normális eloszlást köveztek.
Legyen az első csoport dobásainak változója 
Legyen az a második csoport dobásainak változója 
Legyen a két minta:
Azaz -re egy 20 elemű mintát vettünk, -ra 14 elemű mintát vettünk.
Most a próbának megfelelően a hipotéziseket fogalmazzuk meg.
A nullhipotézis:
Az alternatív vagy ellen hipotézis:
A megengedett elsőfajú hibavalószínűség 0,05.
A próbastatisztika a következő:
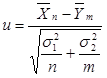
ahol .
Számítsuk ki a mintákból adódó értéket.
A következő adatokból számulunk:
A mintából számolt érték a következő:
.
Az kritikus értékeket az alábbi módon számítjuk:
innen
Az elfogadási tartomány akkor
(-1,95996;+1,95996)
Mivel a mintából mért érték nem esik az elfogadási tartományba így a nullhipotézist elutasítjuk, azaz szignifikánsan különbözik a két osztály átlagos dobóteljesítménye.
Definíció: Egy statisztikai próba szignifikancia szintjének nevezzük azt a legkisebb elsőfajú hibavalószínűséget, amelyre a próbastatisztika alapján a nullhipotézist elvetjük.
Ez a gyakorlati számítások során a próbastatisztikából kapott érték alapján az alternatív hipotézisnek megfelelő valószínűségérték meghatározását jelenti.
Vagyis egy olyan valószínűséget melyre a próbából származtatott érték adja a kritikus tartomány határpontját.
Most döntsünk a szignifikancia szint alapján.
A mintából számolt u érték a következő:
.
A kétoldali hipotézis esetén annak valószínűsége hogy a mintából számított u –érték a baloldali vagy jobboldali kritikus tartomány egyikébe esik egyaránt 0,025.
Ekkor a nullhipotézist elutasítjuk, az alternatív hipotézist fogadjuk el.