Statisztikai hipotézisek vizsgálata
A statisztikai vizsgálatoknak egyik célja lehet, hogy egy minta alapján eldöntsük, hogy egy populációbeli 
változóra vonatkozó sejtés igaz-e vagy sem.
A statisztikai vizsgálatok kapcsán adódó sejtés vonatkozhat például egy valószínűségi változó várható értékére, szórására, két valószínűségi változó függetlenségére, stb.
Ezek a statisztikai hipotézisek. A hipotéziseket statisztikai próbákkal ellenőrizzük.
A hipotézisvizsgálatban két sejtést állítunk fel.
Azt a sejtést, feltevést, amelyet a kiinduláskor igaznak tételezünk fel:
Nullhipotézisnek nevezzük és 
-lal jelöljük.
Felállítunk egy másik sejtést, feltételezést, melyet:
Alternatív hipotézisnek nevezük és 
-val jelölünk.
Nyilván a feladat szempontjából és egymás komplementerei, egyiknek biztosan igaznak kell lennie.
A statisztikai hipotézisvizsgálat célja egy olyan döntést meghozatala, melyben vagy:
elfogadjuk a nullhipotézist, ha a vizsgálatunk ezt bizonyítja, vagy elutasítjuk a nullhipotézist, ezáltal az alternatív hipotézist fogadjuk el.
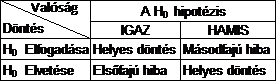
- Így elsőfajú hibát követünk el ha elvetjük a nullhipotézist pedig igaz.
- Másodfajú hibát követünk el ha elfogadjuk a nullhipotézist pedig hamis.
A példák során azt fogjuk megadni, hogy mi a megengedett elsőfajú hibavalószínűség.
A nullhipotézis azt fogalmazza meg hogy a változó egy paraméterére milyen egyenlőséget állítunk.
A alternatív hipotézis jellege alapján lehet baloldali, jobboldali és kétoldali.
Tegyük fel, hogy egy változó valamely paraméterére végezzük a el a hipotézisvizsgálatot.
A hipotézisvizsgálat logikai menete.
- Vegyünk 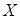-re egy
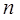elemű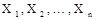 
mintát. - Vegyünk 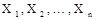mintára egy statisztikát
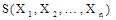-et. - Állítsuk fel a 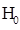nullhipotézist és a 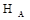alternatív hipotézist.
- Adjuk meg az elsőfajú hiba valószínűségét.
- Ha 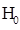igaz akkor 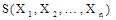eloszlása az eloszlása alapján ismert.
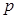alapján és 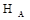jellege alapján határozzuk meg az elfogadási és a kritikus tartományt;- [kritikus az a tartomány melybe legfeljebb az előre megadott elsőfajú hibavalószínűséggel esik a statisztika értéke; a kritikus tartomány komplementere a valósakon az elfogadási tartomány]
- Ha a minta alapján a 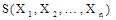az elfogadási tartományba esik akkor 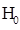-t elfogadjuk