10.1. Alapfeladatok

10.1. gyakorlat. Szerkesszünk trapézt, ha adott a négy oldala!

Megoldás. Induljunk ki a megoldásból, és tegyük fel, hogy  a keresett trapéz, aminek oldalai rendre  és $d$, 27. ábra szerint. Feltesszük, hogy , az  eset vizsgálatát az olvasóra bízzuk. Toljuk el  szárat  vektorral:  pont képe nyilvánvalóan  lesz,  pont képét jelöljük .vel. A feltevések szerint  oldalai rendre ,  és , ezért szerkeszthető. Ezután  pont szerkesztése egyszerű,  egyenesből egy  középpontú,  sugarú kör metszi ki, végül  pontot  pont -ral való eltoltjaként kapjuk.

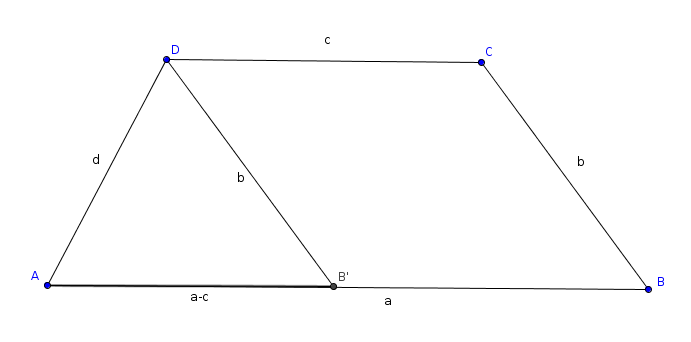
Elemzés: ha  szerkeszthető, akkor egyértelmű a megoldás. 

10.2. gyakorlat. Adott egy  kör, egy  egyenes és egy  pont. Szerkesszünk olyan  egyenest  ponton keresztül, hogy a -lel és -val vett (egyik) metszéspontja által meghatározott szakaszt az  pont felezze.

Megoldás. Tegyük fel, hogy  és  (egyik) közös pontja , , valamint hogy  felezi  szakaszt. Vegyük észre, hogy ez azt jelenti, hogy  illeszkedik az  egyenes -ra vonatkozó  középpontos tükörképére! Ezek alapján a szerkesztés egyszerűen elvégezhető: tükrözzük -t -ra, s keressük meg az  tükörkép -val való metszéspontjait. Ezeket -val összekötve kapjuk a keresett egyenest vagy egyeneseket.

Elemzés: a  körnek és  egyenesnek ,  vagy  metszéspontja lehet, e szerint a feladatnak ,  vagy  megoldása lesz.

10.3. feladat. 

1. Írjunk az adott 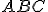 háromszögbe négyzetet, aminek két csúcsa a háromszög $AB$ oldalára, egy-egy csúcsa pedig a háromszög  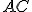ill. 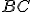 oldalára illeszkedik!
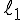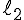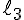2. Írjunk az adott  háromszögbe olyan háromszöget, aminek oldalai párhuzamosak az adott ,  és  egyenesekkel. (Az  háromszög minden oldalára illeszkedik a beírt háromszögg egy-egy csúcsa.)
3. Írjunk az adott  háromszögbe olyan téglalapot, amely oldalainak aránya .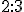

Megoldás. Csak az a) pontot részletezzük, a másik két alfeladat megoldása analóg módon történik. Tekintsük \aref{fig:hban}. ábrát. Jelöljük ki  oldal tetszőleges  pontját, a -ből -re bocsájtott merőleges talppontja legyen . Szerkesszük meg $R$ pontot $AB$-n úgy, hogy  az ábra szerint. Végül szerkesszük meg  pontot, hogy  négyszög négyzet legyen. Természetesen  pont általában nem illeszkedik  oldalra, ezért  nem megoldása a feladatnak.

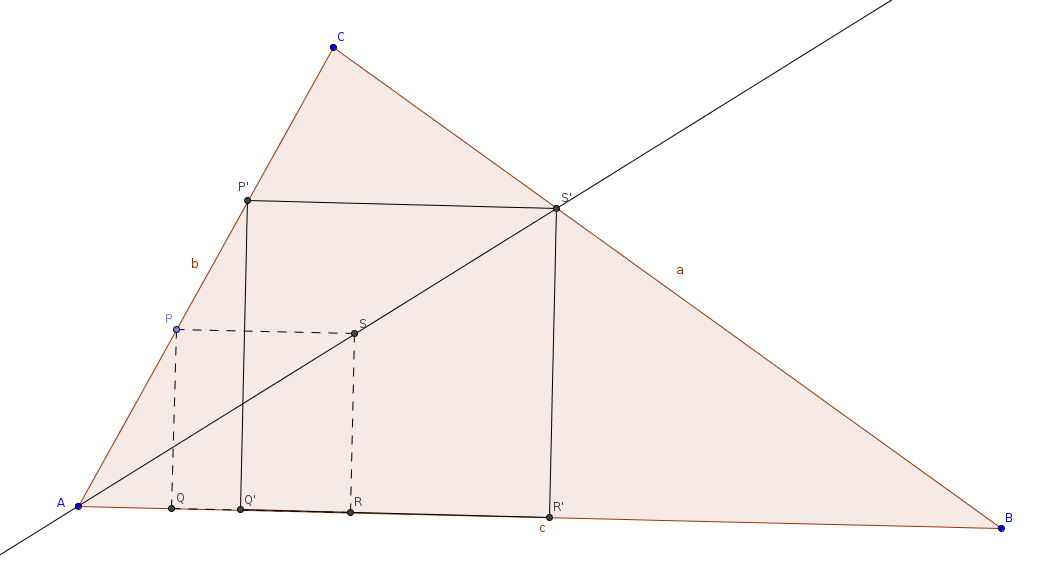
Messe  egyenes a  oldalt -ben. Alkalmazzunk  négyszögre  középpontú,  arányú középpontos hasonlóságot; ez természetesen -t, -be viszi. Legyen  képe . A középpontos hasonlóság szögtartó, ezért  téglalap, valamint aránytartó is, ezért  minden oldala egyenlő. Így  négyzet. A konstrukció miatt , a középpontos hasonlóság megadása miatt pedig  és , ezért  a feladat megoldása.

Elemzés: ha  hegyesszögű, akkor pontosan egy megoldás van. (Miért?) Gondoljuk meg mi történik, ha  tompaszögű.

Tekintsük meg a vonatkozó dinamikus ábrát!

A b) és c) részeknél hasonlóan járjunk el, szerkesszünk egy a keresetthez hasonló alakzatot, ami ``majdnem jó'', vagyis egy kivételével csúcsai illeszkednek a megfelelő oldalakra, majd nagyítsuk fel középpontosan.