10.2. Gyakorlatok
10.4. gyakorlat. Adottak a koncentrikus ![]() és
és ![]() körök. Szerkesszünk olyan
körök. Szerkesszünk olyan ![]() egyenest ami a két körvonalat
egyenest ami a két körvonalat ![]() ,
, ![]() ,
, ![]() és
és ![]() pontokban metszi (az egyenesen ebben a sorrendben), és
pontokban metszi (az egyenesen ebben a sorrendben), és ![]() .
.
Vázlat. Vegyük észre, hogy pl. ![]() pont tetszőlegesen kijelölhető. Ha kiindulunk a megoldásból, akkor
pont tetszőlegesen kijelölhető. Ha kiindulunk a megoldásból, akkor ![]() pont
pont ![]() -re vett tükörképe éppen
-re vett tükörképe éppen ![]() . Így
. Így ![]() illeszkedik
illeszkedik ![]()
![]() -re vett középpontos tükörképére. A szerkesztés 10.2. gyakorlathoz hasonlóan végezhető el. Hány megoldás lesz? Mennyiben térnek el ezek egymástól?
-re vett középpontos tükörképére. A szerkesztés 10.2. gyakorlathoz hasonlóan végezhető el. Hány megoldás lesz? Mennyiben térnek el ezek egymástól? ![]()
10.5. gyakorlat. Adott egy ![]() kör, és rajta [a körvonalon] három pont
kör, és rajta [a körvonalon] három pont ![]() ,
, ![]() és
és ![]() . Szerkesszük meg azt az
. Szerkesszük meg azt az ![]() húrt, amelyet a
húrt, amelyet a ![]() húr felez.
húr felez.
Ötlet. Ha ![]() húrt
húrt ![]() pontból középpontosan kétszeresére nagyítjuk, a nagyított képnek tartalmazni kell
pontból középpontosan kétszeresére nagyítjuk, a nagyított képnek tartalmazni kell ![]() pontot.
pontot. ![]() ,
, ![]() vagy
vagy ![]() megoldás lehet.
megoldás lehet.![]()
10.6. gyakorlat. Szerkesszünk derékszögű háromszöget, ha adott az egyik hegyesszöge és befogóinak összege!
Vázlat. Legyen az adott hegyesszög ![]() , a befogók adott összege
, a befogók adott összege ![]() . Szerkesszünk tetszőleges derékszögű háromszöget, aminek egyik hegyesszöge
. Szerkesszünk tetszőleges derékszögű háromszöget, aminek egyik hegyesszöge ![]() , ennek befogói legyenek
, ennek befogói legyenek ![]() és
és ![]() . Nagyítsuk ezt a derékszögű háromszöget
. Nagyítsuk ezt a derékszögű háromszöget ![]() arányban. Egy megoldás van.
arányban. Egy megoldás van.![]()
10.7. gyakorlat. Az ![]() egyenes egyazon partján adva van az
egyenes egyazon partján adva van az ![]() és
és ![]() pont. Szerkesszünk az
pont. Szerkesszünk az ![]() egyenesen olyan
egyenesen olyan ![]() pontot, amire az
pontot, amire az ![]() és
és ![]() egyenesek ugyanakkora szöget zárnak be
egyenesek ugyanakkora szöget zárnak be ![]() egyenessel.
egyenessel.
Ötlet. Legyen ![]() pont
pont ![]() egyenesre vett tükörképe
egyenesre vett tükörképe ![]() . Az
. Az ![]() ,
, ![]() és a keresett
és a keresett ![]() pontok kollineárisak. Egy megoldás van.
pontok kollineárisak. Egy megoldás van. ![]()
A leckét néhány nehezebb feladattal zárjuk.
10.8. feladat. Az ![]() egyenes egyazon partján adva van az
egyenes egyazon partján adva van az ![]() és
és ![]() pont. Szerkesszünk az
pont. Szerkesszünk az ![]() egyenesen olyan
egyenesen olyan ![]() pontot, amire az
pontot, amire az ![]() egyenes kétszer akkora szöget zár be
egyenes kétszer akkora szöget zár be ![]() egyenessel, mint a
egyenessel, mint a ![]() egyenes.
egyenes.
A megoldás lényegében leolvasható 29. ábráról.

Az utolsó feladatot csak érdeklődő olvasóknak ajánljuk.
10.9. feladat. Adott az ![]() egyenesen az
egyenesen az ![]() pont, és az
pont, és az ![]() egyenesen a
egyenesen a ![]() pont. Szerkesszünk
pont. Szerkesszünk ![]() egyenest, ami olyan
egyenest, ami olyan ![]() ill.
ill. ![]() pontokban metszi az
pontokban metszi az ![]() ill.
ill. ![]() egyeneseket, amikre
egyeneseket, amikre ![]() és
és
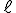 párhuzamos egy adott
párhuzamos egy adott 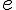 egyenessel.
egyenessel.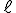 áthalad egy rögzített
áthalad egy rögzített 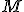 ponton.
ponton.- az
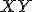 szakasz adott hosszúságú.
szakasz adott hosszúságú. - egy adott
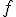 egyenes felezi az
egyenes felezi az 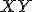 szakaszt.
szakaszt.
Ötletek. Minden alrész megoldása a következő állításon múlik.
Legyenek ![]() két egyenlő hosszú, nem párhuzamos, egymással
két egyenlő hosszú, nem párhuzamos, egymással ![]() szöget bezáró szakaszok. (Szakaszok szögét az őket tartó egyenesek szögeként értelmezzük.) Ekkor létezik egy olyan
szöget bezáró szakaszok. (Szakaszok szögét az őket tartó egyenesek szögeként értelmezzük.) Ekkor létezik egy olyan ![]() pont, hogy az
pont, hogy az ![]() körüli
körüli ![]() vagy
vagy ![]() szögű forgatás
szögű forgatás ![]() -t
-t ![]() -be,
-be, ![]() -t pedig
-t pedig ![]() -ba viszi.
-ba viszi.
Ennek igazolása nem túl nehéz, az ![]() pont az
pont az ![]() szakaszfelező merőlegesének és
szakaszfelező merőlegesének és ![]() szakaszfelező merőlegesének metszéspontjában kell legyen. A feltétel miatt
szakaszfelező merőlegesének metszéspontjában kell legyen. A feltétel miatt ![]() és
és ![]() egybevágóak, hiszen oldalaik páronként egyenlőek, amiből
egybevágóak, hiszen oldalaik páronként egyenlőek, amiből ![]() következik. (Hogyan?) A forgatás nyilvánvalóan
következik. (Hogyan?) A forgatás nyilvánvalóan ![]() egyenest
egyenest ![]() -ba viszi, ezért a forgatás szöge
-ba viszi, ezért a forgatás szöge ![]() vagy
vagy ![]() .
.
Esetünkben ismert ![]() és
és ![]() valamint
valamint ![]() is, ezért (minden lehetséges)
is, ezért (minden lehetséges) ![]() pont megszerkeszthető.
pont megszerkeszthető.
- Legyen az
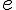 egyenes
egyenes 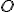 körüli megfelelő elforgatottja
körüli megfelelő elforgatottja 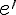 , és
, és 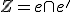 .
. 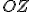 egyenes kimetszi
egyenes kimetszi 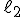 -ből
-ből 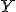 -t. Miért?
-t. Miért? - Legyen
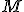 megfelelő elforgatott képe
megfelelő elforgatott képe 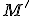 . Az
. Az 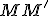 szakasz
szakasz 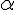 (vagy
(vagy 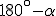 ) szögű látóköríve kimetszi
) szögű látóköríve kimetszi 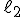 -ből
-ből 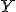 -t. Miért?
-t. Miért? - Mivel
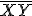 hossza ismert, így
hossza ismert, így 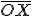 hossza szerkeszthető. Fejezzük be a gondolatmenetet!
hossza szerkeszthető. Fejezzük be a gondolatmenetet! 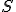 -ből
-ből 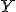 -t egy ismert szögű és ismert arányú forgatva nyújtással kaphatjuk. Hogyan?
-t egy ismert szögű és ismert arányú forgatva nyújtással kaphatjuk. Hogyan?