2.2.1. A körülírt kör középpontja
Az ![]() szakasz szakaszfelező merőlegese azon pontok halmaza a síkon, amelyek
szakasz szakaszfelező merőlegese azon pontok halmaza a síkon, amelyek ![]() -tól és
-tól és ![]() -től egyenlő távolságra vannak. Ismert, hogy az előbb definiált szakaszfelező merőleges egy egyenes, amely illeszkedik az
-től egyenlő távolságra vannak. Ismert, hogy az előbb definiált szakaszfelező merőleges egy egyenes, amely illeszkedik az ![]() szakasz felezőpontjára, és merőleges
szakasz felezőpontjára, és merőleges ![]() egyenesre.
egyenesre.
1. tétel. Az ![]() háromszög oldalfelező merőlegesei egy
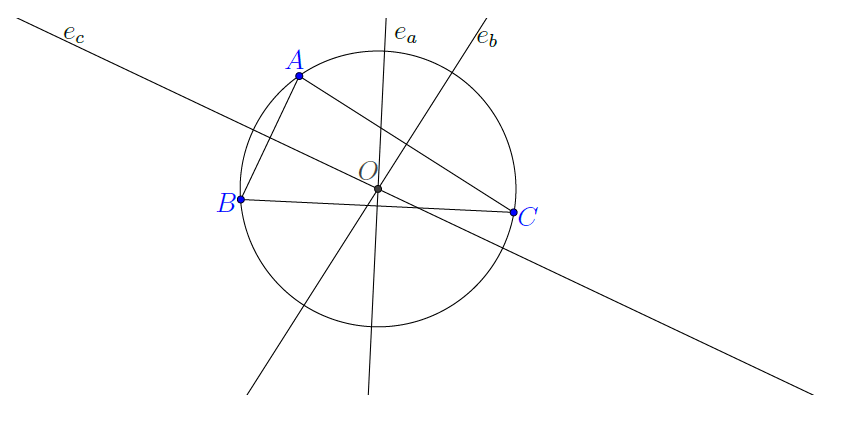
háromszög oldalfelező merőlegesei egy ![]() pontban metszik egymást. Ez a pont a háromszög mindhárom csúcsától ugyanakkora távolságra van. (3. ábra.)
pontban metszik egymást. Ez a pont a háromszög mindhárom csúcsától ugyanakkora távolságra van. (3. ábra.)
Mozgassuk meg az ábrát a GeoGebraTube-on! Mit tapasztalunk, ha a háromszög egyik szögét elkezdjük növelni?
Bizonyítás. Jelölje az oldalfelező merőlegeseket rendre ![]() ,
, ![]() és
és ![]() . Legyen
. Legyen ![]() az
az ![]() és az
és az ![]() egyenesek metszéspontja:
egyenesek metszéspontja: ![]() . Definíció szerint az
. Definíció szerint az ![]() pont egyenlő távolságra van
pont egyenlő távolságra van ![]() és
és ![]() pontoktól (mivel rajta van
pontoktól (mivel rajta van ![]() -n), valamint
-n), valamint![]() egyenlő távolságra van
egyenlő távolságra van ![]() és
és ![]() csúcsoktól (mivel rajta van
csúcsoktól (mivel rajta van ![]() -n). Így az
-n). Így az ![]() pont egyenlő távolságra van az
pont egyenlő távolságra van az ![]() és
és ![]() csúcsoktól is, így rajta van az
csúcsoktól is, így rajta van az ![]() oldalfelező merőlegesen. Valóban, az
oldalfelező merőlegesen. Valóban, az ![]() ,
, ![]() és
és ![]() oldalfelező merőlegesek egy pontban metszik egymást, méghozzá az
oldalfelező merőlegesek egy pontban metszik egymást, méghozzá az ![]() pontban, amely mindhárom csúcstól ugyanakkora távolságra van.
pontban, amely mindhárom csúcstól ugyanakkora távolságra van.![]()
Tekintsük 1. Tételben szereplő ![]() háromszöget, és az
háromszöget, és az ![]() pontot, valamint legyen
pontot, valamint legyen ![]() .
.
Az ![]() körüli,
körüli, ![]() sugarú körvonal tartalmazza az
sugarú körvonal tartalmazza az ![]() ,
, ![]() és
és ![]() pontok mindegyikét, ezért a háromszög körülírt körének nevezzük. A körülírt kör az egyetlen mindhárom csúcsot tartalmazó körvonal.
pontok mindegyikét, ezért a háromszög körülírt körének nevezzük. A körülírt kör az egyetlen mindhárom csúcsot tartalmazó körvonal.