2.2.3. A magasságpont

A háromszög egyik csúcsából a szemközti oldalegyenesre bocsájtott merőleges egyenest a háromszög magasságvonalának nevezzük. A magasságvonal és az oldalegyenes metszéspontja a magasság talppontja. A csúcsot a talpponttal összekötő szakaszt a háromszög magasságának nevezzük. A magasság szó gyakran ennek a szakasznak a hosszát is jelenti. Ez másképp mondva a csúcs távolsága a szemközti oldalegyenestől.

A magasság fogalmának bevezetését a háromszögre érvényes legelső területformulánk motiválhatja. Ha a háromszög csúcsával szemközt hosszú oldala van, és a hozzájuk tartozó magasság , akkor a háromszög területe

3. tétel. A háromszög magasságvonalai egy pontban metszik egymást. Ezt a pontot a háromszög magasságpontjának nevezzük.

Tekintsük meg a GeoGebraTube-on a vonatkozó dinamikus ábrát! A bizonyítás előtt ismételjük át a paralelogramáról tanult alapvető ismereteinket a Wikipédia alapján!

Bizonyítás. Tekintsük 4. ábrát. Jelölje a magasságvonalakat rendre , és . Húzzunk párhuzamost -val -n keresztül, -vel -n keresztül, és -vel -n keresztül. Ezek az egyenesek meghatároznak egy nagyobb

4. ábra. A háromszög magasságpontja

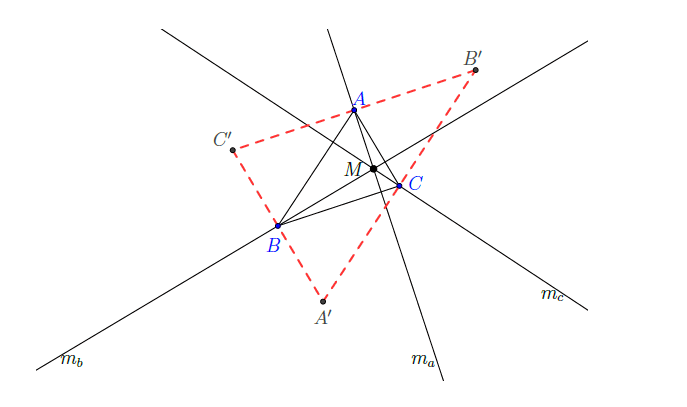
háromszöget, ennek csúcsait jelölje , és az ábra szerint. A négyszög paralelogramma, mivel és . Hasonlóan kapjuk, hogy négyszög is paralelogramma. Így . Ezért pont felezi szakaszt. Továbbá, , valamint , így . Kaptuk, hogy a szakasz felező merőlegese. Hasonlóan megmutatható, hogy az szakasz felező merőlegese, míg az szakasz felező merőlegese. Az , és egyenesek az oldalfelező merőlegesei, így valóban egy pontban metszik egymást.