11.1. A Sylvester-Gallai tétel

Ebben a szakaszban egy nevezetes illeszkedési tételt ismerünk meg, amely Erdős Pál egyik kedvenc feladata volt.

Olvassunk utána Erdős Pál életútjának az interneten!

28. tétel (Sylvester-Gallai tétel). Adott  pont a síkon. Ekkor vagy az összes adott pont illeszkedik egy egyenesre, vagy van egy olyan egyenes, amire közülük pontosan kettő illeszkedik!

A tételt Sylvester tűzte ki az 11851-es problémaként 1893-ban a The Educational Times-ban. Sokan a kombinatorikus geometria egyik kiindulópontjának tekintik. A teljes megoldás meglepően sokáig váratott magára, 1944 környékén oldotta meg Erdős Pál közeli barátja, Lovász László későbbi témavezetője, Gallai Tibor. A problémának a mai napig aktív utóélete van. Később a tételre több különböző bizonyítás született, az alábbi Kelly nevéhez fűzödik.

Bizonyítás. Legyenek az adott pontok , és tekintsük az összes olyan egyenest, amire az adott pontok közül legalább kettő illeszkedik: . (Ilyen egyenesből valóban csak véges sok van.)

A bizonyítást indirekt végezzük. Az indirekt bizonyítás lényege, hogy feltesszük a bizonyítandó állítás tagadását, és ebből ellentmondásra jutunk a kiindulási feltételekkel.

Olvassuk el a Wikipédia szócikkét az indirekt bizonyításról!

Az állítás tagadása esetünkben azt mondja, hogy a  pontok nem kollineárisak, és nincs olyan egyenes, amire közülük pontosan kettő illeszkedik.

Utóbbi feltételt jelöléseinkkel úgy is megfogalmazhatjuk, hogy az  egyenesek mindegyikére legalább három pont illeszkedik.
Tekintsük az összes lehetséges  párt, ahol  és . Minden ilyen párra lemérjük a  pont és az  egyenes  távolságát. Ha , akkor természetesen . Mivel azonban a feltevésünk szerint a  pontok nem kollineárisak, így létezik olyan pár, amire a távolság szigorúan pozitív. Tekintsük az egyik olyan párt, amire a távolság pozitív, de az ilyenek között a lehető legkisebb, minimális. Ilyen pár

van. (Esetleg több is, ilyenkor szabadon válasszunk egyet.) A jelölések esetleges újraindexelésével elérhetjük, hogy a választott minimális távolságú pár a  legyen. Formulával röviden ez így írható: 

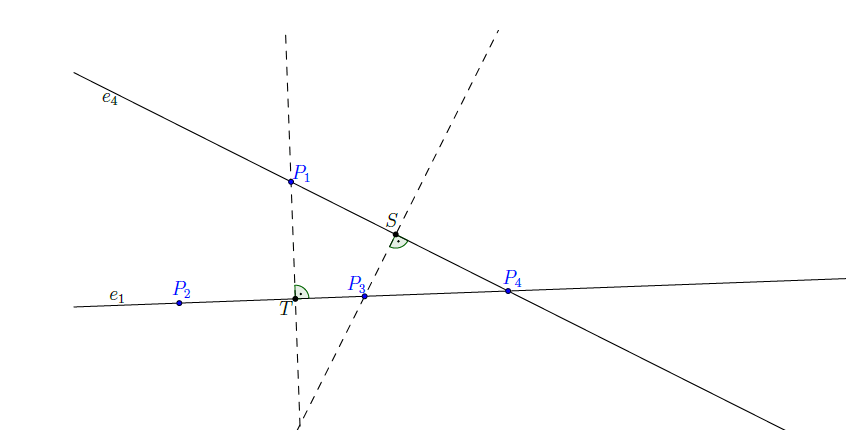
Tekintsük 30. ábrát! Legyen  a -ből -re bocsájtott merőleges talppontja. Az indirekt feltevés szerint az  egyenesre legalább három adott pont illeszkedik. Feltehetjük, hogy  és  három -re ebben a sorrendben illeszkedő pont, az ábra szerint. Feltehető továbbá az is, hogy  nem választja el -t és -t. (Ha elválasztja, vagyis  a  szakasz belső pontja, akkor  szerepét  veszi át.) A  egyenest felsoroltuk, feltehetjük, hogy épp -gyel jelöltük. Végül, legyen  a -ból -re bocsájtott merőleges talppontja.
A bizonyítás következő lépését az olvasóra bízzuk.

11.1. gyakorlat. Mutassuk meg, hogy a fenti jelölésekkel !

A 11.1. gyakorlatból a tétel azonnal következik. Kaptuk ugyanis, hogy , ami ellentmond annak, hogy  a lehető legkisebb. Ezzel az indirekt bizonyítást befejeztük, ellentmondásra jutottunk, az indirekt feltevésünk szükségképpen hamis, tehát a tétel állítása igaz.
A Sylvester-Gallai tétel egyik legismertebb következménye a következő feladat.

11.2. feladat. Adott  nem kollineáris pont a síkon. Mutassuk meg, hogy legalább  olyan egyenes van, amire az adott pontok közül legalább kettő illeszkedik!

Megoldás. A bizonyítást teljes indukcióval végezzük. A teljes indukciós bizonyításokban általában egy olyan állítást bizonyítunk, amelyik függ az  természetes számtól. Lényege, hogy először az  kis értékeire az állítást külön igazoljuk. Majd második lépésként azt mutatjuk meg, hogy ha az állítás valamilyen -re igaz, akkor -re is teljesül.

Olvassuk a teljes indukcióról szóló Wikipédia szócikket!

Visszatérve a feladat megoldására, az  esetén az állítás nyilvánvaló.

Tegyük fel, hogy az állítást már igazoltuk  esetén, és most bizonyítsuk -re.

Tekintsük a  nem kollineáris pontokat. A Sylvester-Gallai tétel szerint feltehetjük, hogy  egyenesre a  pontok egyike sem illeszkedik. Két eset lehetséges.

Ha a  pontok kollineárisak, akkor a feltevés szerint  erre az egyenesre nem illeszkedik, így -t a  pontok mindegyikével összekötve éppen  különböző egyenest kapunk, a  egyenes pedig ezektől is különböző, így valóban megvan a  meghatározott egyenes.
Ha a  pontok nem kollineárisak, akkor az indukciós feltevés szerint meghatároznak legalább  különböző egyenest. Ezek között  biztosan nem szerepel, hiszen  egyenesre a  pontok egyike sem illeszkedik. Így az állítás ebben az esetben is teljesül -re.
Ezzel az indukciós lépést befejeztük, és a bizonyítás teljes.
A Sylvester-Gallai tétel duálisa a következő feladat, amit a téma iránt érdeklődő hallgatóknak ajánlunk.

11.3. feladat. Adott $n$ egyenes síkon úgy, hogy nincsen köztük két párhuzamos, és nem illeszkednek egyetlen pontra. Ekkor létezik olyan pont, ami az adott egyenesek közül pontosan kettőre illeszkedik.

A feladat megoldása valamint egészen aktuális kutatási eredmények találhatóak Jonathan Lechner (angol nyelvű) PhD disszertációjában.