3.3. Nevezetes tételek derékszögű háromszögekre

8. tétel (Thalész-tétel). Ha egy kör átmérőjének  és  végpontját összekötjük a körív -tól és -től különböző tetszőleges  pontjával, akkor az  -nél lévő szöge derékszög lesz.

Bizonyítás. Tekintsük 7. ábrát. Az  és  háromszögek egyenlőszárúak, hiszen  a kör sugara. Ezért az alapon fekvő szögek egyenlőek  ill. . Kihasználva, hogy a háromszög belső szögeinek összege , kapjuk, hogy , s így  valóban.

9. tétel (Thalész-tétel megfordítása). A derékszögű háromszög köré írt kör középpontja az átfogó felezőpontja.

A megfordítás igazolását az érdeklődő olvasóra hagyjuk.

10. tétel (Magasságtétel). Az  derékszögű háromszögben az átfogóhoz tartozó  magasság az átfogót két,  és  hosszú darabra bontja. Ekkor .

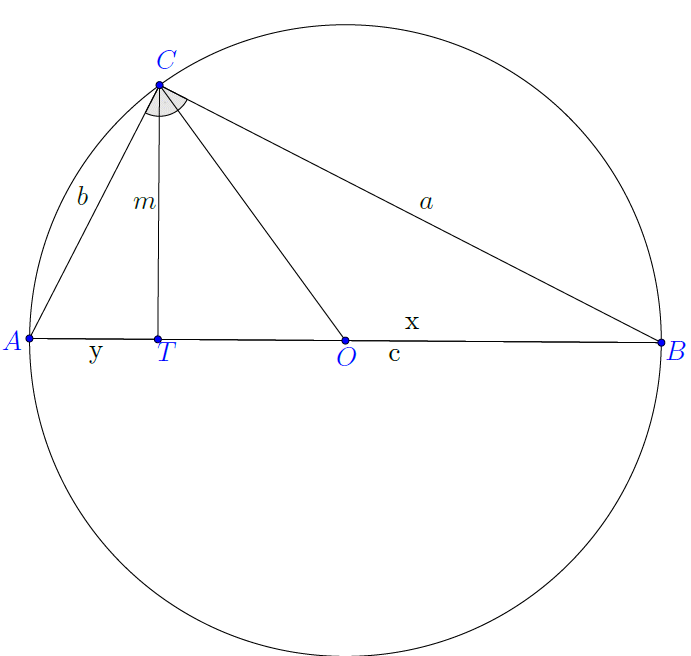
11. tétel (Befogótétel). Az  derékszögű háromszögben az átfogóhoz tartozó  magasság talppontja legyen ,  és . Ekkor  és . 

3.4. gyakorlat. Bizonyítsuk be a 10. és 11. tételeket a Pitagorász-tétel segítségével!

10. és 11. tételeket a kurzus folyamán később más úton is igazoljuk.

3.5. gyakorlat. Bizonyítsuk be a Thalész-tételt a Pitagorász-tétel és megfordítása segítségével!

Megoldási tipp: írjuk fel a Pitagorász-tételt 7. ábrán szereplő derékszögű háromszögekre, majd rendezzük a kapottakat.

Kapcsolódó Wikipédia-szócikkek: Pitagorász-tétel, Thalész-tétel és megfordítása.