5.2.1. Eltolás
Szemléletesen "eltolásnál minden pontot ugyanabba az irányba, ugyanannyival mozgatunk el". Így elegendő egyetlen ![]() pontot és
pontot és ![]() képét megadni, hogy leírjuk az eltolást. Precízebben: rögzítsük
képét megadni, hogy leírjuk az eltolást. Precízebben: rögzítsük ![]() és
és ![]() pontokat. A
pontokat. A ![]() eltolást a következőképpen definiáljuk:
eltolást a következőképpen definiáljuk: ![]() , továbbá bármely
, továbbá bármely ![]() pont képe az a
pont képe az a ![]() , amire
, amire ![]() négyszög - ebben a sorrendben - paralelogramma (vagyis
négyszög - ebben a sorrendben - paralelogramma (vagyis ![]() és
és ![]() , lásd 12. ábra).
, lásd 12. ábra).
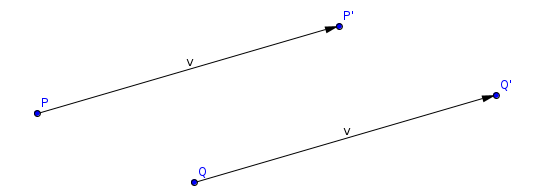
Ha ![]() rajta van
rajta van ![]() egyenesen, többféleképpen is teljessé tehetjük a definíciót. Legkényelmesebb azt mondani, hogy tekintsünk egy
egyenesen, többféleképpen is teljessé tehetjük a definíciót. Legkényelmesebb azt mondani, hogy tekintsünk egy ![]() pontot, és annak (már definiált)
pontot, és annak (már definiált) ![]() képét. A
képét. A ![]() képe az a
képe az a ![]() , amire
, amire ![]() négyszög ebben a sorrendben paralelogramma.
négyszög ebben a sorrendben paralelogramma.
A definíció így is némileg körülményes, és az is meggondolásra szorul, hogy helyes-e. (Például az utolsó lépésben nem függ-e ![]() az
az ![]() választásától, stb..)
választásától, stb..)
A definíció is erősen motiválja, hogy bevezessük a vektor fogalmát. Ezt a kurzusban csak érintőlegesen tesszük meg: ha ![]() egy eltolás (az előbb definiált értelemben), akkor minden
egy eltolás (az előbb definiált értelemben), akkor minden ![]() pontra igaz, hogy a
pontra igaz, hogy a ![]() szakasz ugyanolyan hosszú és ugyanolyan irányú. Ezt a tényt ragadjuk meg a vektor fogalmával, s azt mondjuk, hogy az eltolás vektora
szakasz ugyanolyan hosszú és ugyanolyan irányú. Ezt a tényt ragadjuk meg a vektor fogalmával, s azt mondjuk, hogy az eltolás vektora ![]() . A vektor definíciójára felsőbb matematikai tanulmányaink során még többször is vissza fogunk térni.
. A vektor definíciójára felsőbb matematikai tanulmányaink során még többször is vissza fogunk térni.
Tekintsük meg a GeoGebraTube-on az eltolásról készült dinamikus ábrát!
5.5. gyakorlat. Az előző szakaszok, valamint középiskolai tanulmányaink alapján gyűjtsük össze az eltolás minél több ismert tulajdonságát!
Látogassunk el a vonatkozó Wikipédia oldalra!
5.6. gyakorlat. A síkon végrehajtunk egymás után két eltolást ![]() és
és ![]() vektorokkal. Egyetlen transzformációval hogyan helyettesíthető ez a művelet?
vektorokkal. Egyetlen transzformációval hogyan helyettesíthető ez a művelet?
5.7. gyakorlat. Kisérletezzünk a GeoGebrával! Helyettesíthető-e egy eltolás két ill. három tengelyes tükrözés egymásutánjával?
Tipp: mi történik, ha két egymással párhuzamos tengelyre tükrözünk egymás után?