1.2. Három térelem kölcsönös helyzete
Három térelem kölcsönös helyzetét már feladatokon keresztül dolgozzuk fel.
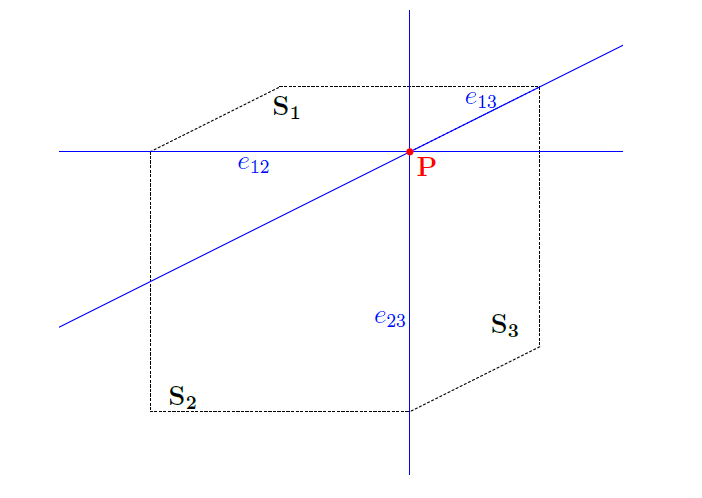
1.1. gyakorlat. Mutassuk meg, hogy ha három sík közül bármely kettő egy egyenesben metszi egymást, és a metszetegyenesek közül valamely kettő egy ![]() pontban metszi egymást, akkor a harmadik metszetegyenes is illeszkedik
pontban metszi egymást, akkor a harmadik metszetegyenes is illeszkedik ![]() -re.
-re.
Legyenek ![]() ,
, ![]() és
és ![]() a vizsgált síkok, amelyek közül bármely kettő egy egyenesben metszi egymást.
a vizsgált síkok, amelyek közül bármely kettő egy egyenesben metszi egymást.
Az ![]() , az
, az ![]() illetve az
illetve az ![]() egyenesek legyenek rendre
egyenesek legyenek rendre ![]()
![]() és
és ![]() .
.
Továbbá legyen ![]() a metszéspont. Másképpen,
a metszéspont. Másképpen, ![]() az a pont, amire
az a pont, amire ![]() és
és ![]() . (Lásd 2. ábra.)
. (Lásd 2. ábra.)
Hasonlóan,
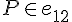 és
és 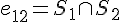 miatt
miatt 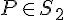 ;
;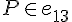 és
és 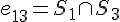 miatt
miatt 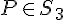 .
.
Következésképpen ![]() is, azaz $
is, azaz $![]() . Tehát a
. Tehát a ![]() pont rajta van az
pont rajta van az ![]() ,
, ![]() és
és ![]() síkok által meghatározott metszetegyenesek mindegyikén.
síkok által meghatározott metszetegyenesek mindegyikén.![]()
1.1. gyakorlat megoldását felhasználva oldjuk meg a következő gyakorlatokat önállóan!
1.2. gyakorlat. Adott 3 páronként egyenesben metsző sík. A három metszésvonaluk közül kettő párhuzamos. Mutassuk meg, hogy ekkor bármely két metszésvonal párhuzamos!
1.3. gyakorlat. A párhuzamos ![]() és
és ![]() síkokat az
síkokat az ![]() sík rendre
sík rendre ![]() és
és ![]() egyenesekben metszi. Mutassuk meg, hogy
egyenesekben metszi. Mutassuk meg, hogy ![]() !
!
1.4. gyakorlat. Az ![]() egyenes párhuzamos a metsző
egyenes párhuzamos a metsző ![]() és
és ![]() síkok mindegyikével. Mutassuk meg, hogy
síkok mindegyikével. Mutassuk meg, hogy ![]() párhuzamos
párhuzamos ![]() egyenessel is!
egyenessel is!
Megoldás. Csak azt az esetet tárgyaljuk, amikor ![]() nem illeszkedik az adott
nem illeszkedik az adott ![]() és
és ![]() síkok egyikére sem. A többi eset hasonló, ezek kidolgozását az olvasóra bízzuk.
síkok egyikére sem. A többi eset hasonló, ezek kidolgozását az olvasóra bízzuk.
Legyen ![]() egy tetszőleges pont, és legyen
egy tetszőleges pont, és legyen ![]() a
a ![]() és
és ![]() által feszített sík.
által feszített sík. ![]() illeszkedik
illeszkedik ![]() -re, mivel
-re, mivel ![]() mindkét síkon rajta van, másrészt párhuzamos is
mindkét síkon rajta van, másrészt párhuzamos is ![]() -vel, hiszen
-vel, hiszen ![]()
síkra ![]() és
és ![]() is illeszkedik, de közös pontjuk nem lehet
is illeszkedik, de közös pontjuk nem lehet ![]() miatt. Így
miatt. Így ![]() az az egyetlen egyenes, ami
az az egyetlen egyenes, ami ![]() -re illeszkedik, és párhuzamos
-re illeszkedik, és párhuzamos ![]() -vel. Hasonlóan érvelhetünk
-vel. Hasonlóan érvelhetünk ![]() -re, s így kapjuk hogy
-re, s így kapjuk hogy ![]() . Mivel
. Mivel ![]() , így az állítást beláttuk.
, így az állítást beláttuk.![]()