9.3. További alapvető euklidészi szerkesztések

Ebben a szakaszban néhány további alapvető fontosságú szerkesztést ismertetünk feladatokon keresztül. Ezek megoldását nem, vagy csak vázlatosan ismertetjük.

9.7. gyakorlat. Adott egy  szakasz.

1. Osszuk fel 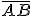-t két olyan darabra, amik hosszai úgy aránylanak egymáshoz, mint 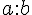. (Ahol  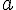és 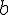 két adott szakasz.)
2. Osszuk fel 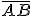-t 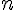 egyenlő részre!

Megoldás. Csak az a) rész megoldását ismertetjük. Húzzunk egy tetszőleges $A$ kezdőpontú segédfélegyenest, és ezen vegyük fel  és  pontokat úgy, hogy  és . Szerkesszünk -vel párhuzamost -n keresztül. Ez a párhuzamos szelők tétele miatt  szakaszt egy olyan  belső pontban metszi, amire . A részletek kidolgozását az olvasóra bízzuk, lásd 25. ábra. 

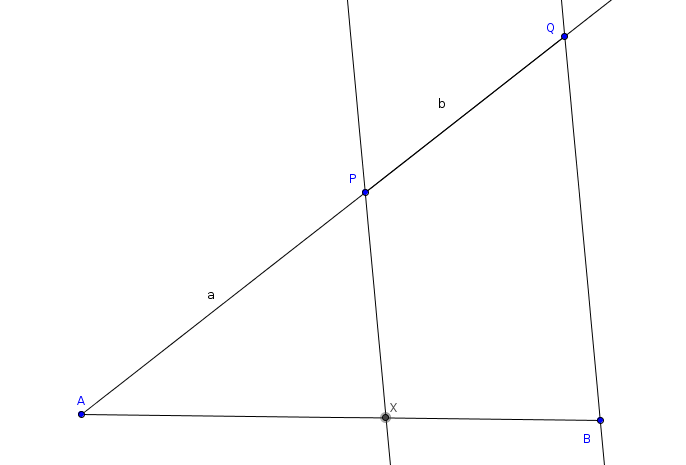
A 9.7. gyakorlat alapján oldjuk meg a következő feladatot:

9.8. gyakorlat. Szerkesszük meg egy  pont  középpontú,  arányú középpontos hasonlóság melletti képét, ahol  és  adott szakaszok!

9.9. gyakorlat. Szerkesszünk háromszöget, ha adott

1. egy oldala, és rajta fekvő két szöge.
2. két oldala, és a közbezárt szögük.
3. két oldala, és egy tetszőleges szöge.

Megjegyzés. A feladat megoldását az olvasóra bízzuk. Felhívjuk azonban a figyelmet a következőkre: az a) résznek pontosan akkor van megoldása, ha a megadott két szög összege kisebb, mint , és ilyenkor (izometria erejéig)  pontosan egy megoldás van. A b) résznek mindig pontosan egy megoldása van (izometria erejéig). A c) résznek lehet egy vagy két megoldása is!

9.10. gyakorlat. Adott egy  és egy  hosszúságú szakasz. Szerkesszünk  hosszúságú szakaszt!

Megoldás. Vegyük fel egy egyenesre egymás után az adott  hosszúságú, és  hosszúságú szakaszukat úgy, hogy  és . Az  szakasz felezőpontja legyen , s állítsunk  merőlegest -ben -re. Messe  az  átmérőjű,  sugarú kört  és  pontokban. A Thalész-tétel szerint  derékszög, és így -re érvényes a magasság-tétel: , vagyis . 

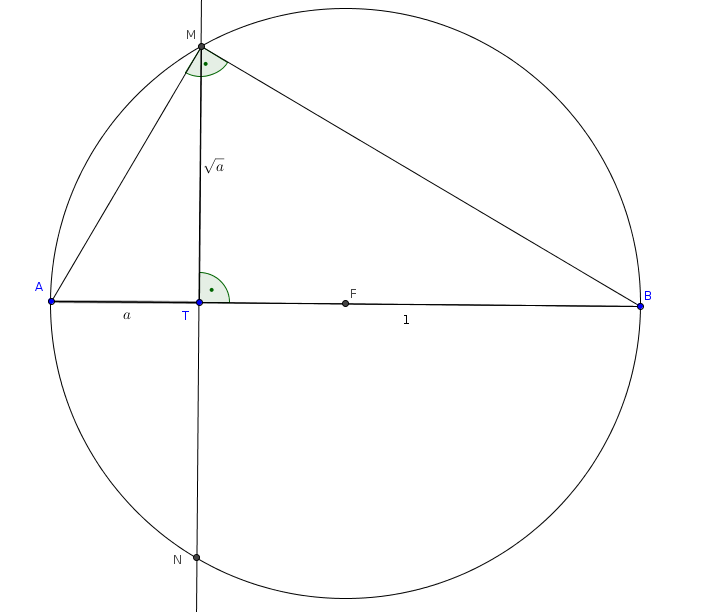
Megjegyzés. Ha egy derékszögű háromszög átfogója , egyik befogója , akkor a Pitagorász-tétel szerint a másik befogóra  adódik. A szerkesztés ez alapján is elvégezhető.

9.11. gyakorlat. Szerkesszünk -os, -os, -os, -os és -os szögeket!

9.12. gyakorlat. Szerkesszük meg egy  pont, egy  egyenes és egy  kör

1. adott 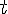 tengelyre vonatkozó tükörképet;
2. adott 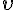 vektorral vett eltoltját;
3. adott 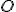 pont körüli, adott  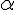szöggel való elforgatottját!

9.13. feladat. Szerkesszünk szabályos ötszöget!

Tekintsük meg a szabályos ötszög szerkesztéséről készült videót a youtube-on!

Megjegyzés. A szabályos ötszög belső szögei -osak, ennek és a fentiek segítségével szerkeszthető  minden egész számú többszöröse. (Hogyan?) Mély matematikai eszközökkel kimutatható, hogy más egész fokos szögek nem szerkeszthetőek körzővel és vonalzóval.