4.2. Párhuzamos szelők és szelőszakaszok tétele
A következő tétel kulcsfontosságú elméleti jelentőségű.
14. tétel (Párhuzamos szelők tétele). Egy 
csúcsú szög szárait messék a párhuzamos 
és 
egyenesek rendre 
és 
, ill. 
és 
pontokban. (Lásd 8. ábra.) Ekkor
Bizonyítás. Az 
és az 
-ból induló magassága megegyezik, jelölje ezt 
. Így
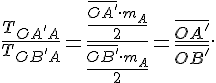
Hasonlóan indokolhatunk 
és 
esetén, és így nyerjük, hogy
Belátjuk, hogy 
, így a tétel a fenti két egyenlőségből azonnal következik. Ehhez vegyük észre, hogy 
, hiszen 
alap közös, és a hozzá tartozó magasság a két háromszögben egyenlő 
miatt. Így
4.6. gyakorlat. Készítsünk a párhuzamos szelők tételét szemléltető dinamikus ábrát.
A tételt felhasználva bizonyítsuk a következő, általánosabb alakot.
4.7. gyakorlat. Egy csúcsú szög szárait messék a párhuzamos , , 
és 
egyenesek rendre és , és , 
és 
, ill. 
és 
pontokban. Ekkor
Ötlet. A párhuzamos szelők tételének előbb igazolt alakja szerint létezik valamilyen 
valós szám, hogy 
, ahol 
helyén állhat , , vagy . 
Az 
, 
, stb. szakaszokat szokás szelőszakaszoknak is nevezni. Ezek hosszáról is állíthatunk hasonlót, mint az előbbi tételekben.
15. tétel (Párhuzamos szelőszakaszok tétele). Egy csúcsú szög szárait messék a párhuzamos és egyenesek rendre és , ill. és pontokban. (8. ábra.) Ekkor
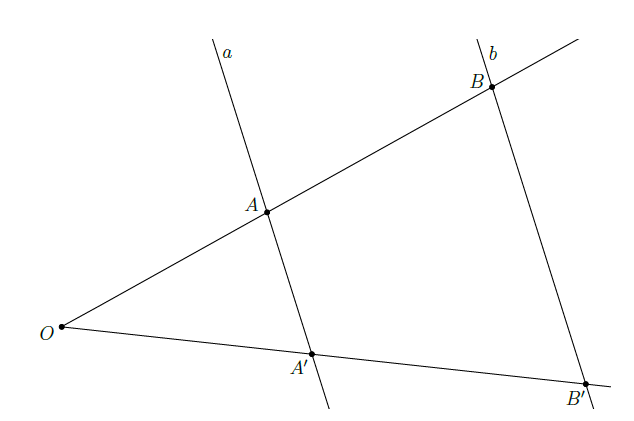
Bizonyítás. Húzzunk párhuzamost -n keresztül 
-vel, és messe ez -t -ben, lásd 9. ábra. A párhuzamos egyenespárok miatt 
paralelogramma, ezért 
. Alkalmazzuk a párhuzamos szelők tételének erősebb alakját (4.7. gyakorlat) a csúcsú 
szögre, és az 
és egyenesekre:
ahogy állítottuk. 
A tételek megfordíthatóak.
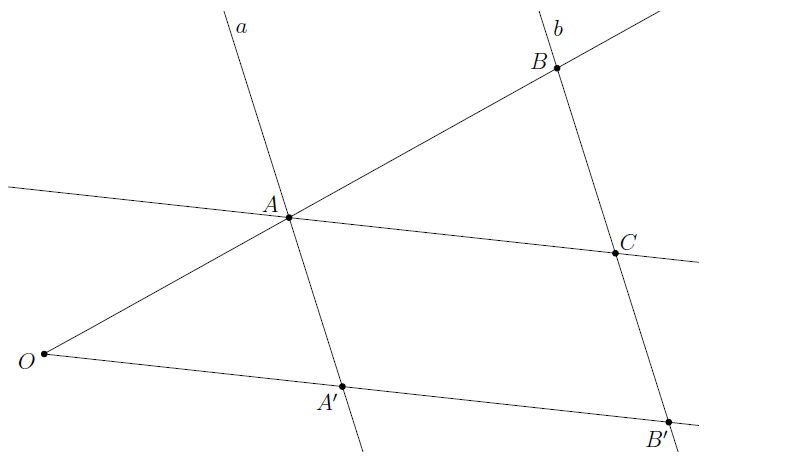
16. tétel (Párhuzamos szelők tételének megfordítása). Egy csúcsú szög szárait messék az és egyenesek rendre és , ill. és pontokban. (Lásd 8. ábra.) Tegyük fel, hogy
Ekkor és párhuzamosak.
Bizonyításvázlat. Húzzunk 
párhuzamost keresztül -vel, messe ez az egyenes szögszárat 
-ben. Felírva a párhuzamos szelők tételét -re és -re, valamint felhasználva a feltételt, 
azonnal adódik.
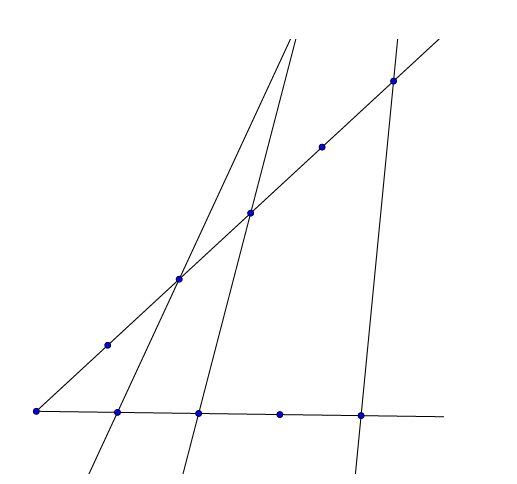
Vigyázat! A párhuzamos szelők tételének erősebb alakja lényegében nem fordítható meg. Ehhez tekintsük a 10. ábrát!
4.8. gyakorlat. Fordítsuk meg a párhuzamos szelőszakaszok tételét! Igaz-e a megfordítás? Ha nem sikerül válaszolni, kutakodjunk a könyvtárban vagy az Interneten!
Tipp: Tekintsük újra a 8. ábrát. Van-e olyan 
pont az szögszáron, amire 
?