5.1. Tengelyes tükrözés

Rögzítsünk egy  egyenest a síkon, és tekintsünk egy tetszőleges  pontot. Ekkor pontosan egy olyan  pont létezik, hogy  a  szakaszfelező merőlegese. (Ha , akkor megállapodás szerint .) A  pontot a  pont -re vonatkozó tükörképének nevezzük. Azt a transzformációt, amely minden ponthoz hozzárendeli az -re vonatkozóz tükörképét, az -re vett tengelyes tükrözésnek nevezzük.

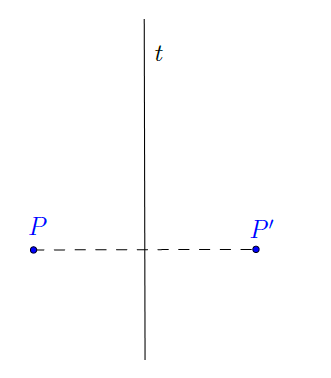
Dinamikus ábra a tengelyes tükrözésről a GeoGebraTube-on.
Használjuk fel a szakaszfelező merőleges korábbi definícióját, valamint a háromszögek egybevágóságának tanult alapeseteit, és ezek segítségével igazoljuk az alábbi állítást.

 5.1. gyakorlat. Ha a  és  pontok -re vonatkozó tükörképei rendre  és , akkor .

Megoldásvázlat. Tegyük fel, hogy  egyenes  pontban metszi az  tengelyt, továbbá legyen  egy -től
különböző pont a tengelyen. Mutassuk meg, hogy  és .
Ebből az állítás következik. (Miért?) Mi a helyzet, ha ? 

A fenti állítást úgy is mondjuk röviden, hogy a tengelyes tükrözés távolságtartó, hiszen ha tekintünk két tetszőleges pontot, akkor tükörképeik távolsága
megegyezik az eredeti pontok (őspontok) távolságával. A következő állításban összefoglaljuk a tengelyes tükrözés legfontosabb tulajdonságait.

17. tétel (A tengelyes tükrözés alaptulajdonságai). A tengelyes tükrözés

1. távolságtartó;
2. szögtartó;
3. területtartó;
4. a tengely pontjait fixen hagyja;
5. a tengelyhez tartozó két (nyílt) félsíkot felcseréli;
6. involúció, azaz kétszer egymás után végrehajtva minden pont visszakerül eredeti helyére;
7. a tengelyre merőleges egyeneseket önmagukba viszi.

5.2. gyakorlat. (a) Piroska a nagymamához készül. Mi a legrövidebb út, ha közben még a folyóparton a korsóját is meg kell töltenie friss vízzel? (Piroska és a nagymama egy-egy pont, a folyó egy egyenes által határolt félsík, ami nem tartalmazza Piroskát és a nagymamát.)

1. Egy hegyesszögtartományban adott egy 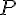 pont. Mi a legrövidebb út, ami a szög mindkét szárát érinti, majd visszatér 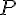-be?
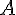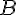2. Egy hegyesszögtartományban adottak  és  pontok. Mi a legrövidebb 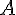-ból 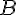-be vezető út, ami a szög mindkét szárát érinti?

Megoldás.
a) Jelölje  Piroskát,  a nagymamát,  a folyót. Legyen  -re vonatkozó tükörképe , és messe  egyenes -t -ben. Egy tetszőleges  pontra 

Ez mutatja, hogy a  és  szakaszokból álló (töröttvonal) séta a legrövidebb.

b) (Vázlat.) Tükrözzük -t a szögszárakra, és a kapott pontokat kössük össze egy egyenessel. Ez az egyenes messe a szögszárakat -ben és -ban.  háromszög alakú séta a megoldás, az indoklás hasonlóan történhet az a) részhez.

c) (Vázlat.) Az  pontot az egyik, -t a másik szögszárra tükrözzük, majd a b) résszel analóg módon indoklunk. Vigyázat! Ez esetben kettő lehetőséget kapunk, amik közül a rövidebbet kell majd választanunk. (Nem mindegy, hogy az -ból induló séta először melyik szögszárat látogatja meg.)