3.2. Pitagorász-tétel
Talán az egész matematika leghíresebb tétele a következő.
5. tétel (Pitagorász-tétel). Derékszögű háromszögben az átfogó négyzete megegyezik a befogók négyzeteinek összegével:
![]()
A tételre (állítólag) több mint 200 féle különböző bizonyítás ismert. Mi az előkészületeink után kényelmes helyzetben vagyunk.
Bizonyítás. A 3.1. és 3.2. gyakorlatok alapján felírhatjuk a beírt kör sugarát kétféleképpen:
![]()
Felhasználva, hogy ![]() , a tétel következik a fenti egyenlőségből, ha mindkét oldalt megszorozzuk
, a tétel következik a fenti egyenlőségből, ha mindkét oldalt megszorozzuk ![]() -vel.
-vel.![]()
Tekintsük meg a tétel egy látványos szemléltetését a youtube-on.
3.3. gyakorlat. Számítsuk ki az ![]() oldalhosszúságú szabályos háromszög területét!
oldalhosszúságú szabályos háromszög területét!
A tétel megfordítható, a megfordítást később igazoljuk:
6. tétel (Pitagorász-tétel megfordítása). Ha egy háromszög két oldalhosszának négyzetösszege egyenlő a harmadik oldal hosszának négyzetével, akkor a háromszög derékszögű.
Végül egy nevezetes tételt tűzünk ki gyakorlatként, ami a Pitagorász-tétel következménye.
7. tétel (Paralelogramma-tétel). Mutassuk meg, hogy a paralelogramma oldalainak négyzetösszege, megegyezik az átlóinak négyzetösszegével! Azaz, ha egy paralelogramma oldalai ![]() és
és ![]() , átlói pedig
, átlói pedig ![]() és
és ![]() , akkor
, akkor
![]()
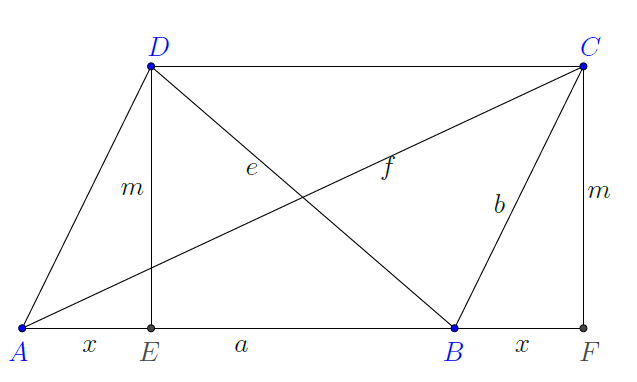
Bizonyítás. Írjuk fel a Pitagorász-tételt 6. ábrán látható derékszögű háromszögekre:![]() -re kapjuk, hogy
-re kapjuk, hogy ![]() .
.
![]() -re
-re ![]() , míg
, míg ![]() -re
-re ![]() .
.
Utóbbi kettőt összeadva, és a négyzetreemeléseket elvégezve, egyszerűsítve adódik, hogy ![]() . Végül ebbe a legelső Pitagorász-tételt beírva kapjuk a paralelogramma-tételt:
. Végül ebbe a legelső Pitagorász-tételt beírva kapjuk a paralelogramma-tételt: ![]()
![]()
Paralelogramma-tétel a GeoGebraTube-on.