13. Nevezetes tételek, egyenlőtlenségek, szélsőértékfeladatok

A kurzus zárásaként összegyűjtöttünk néhány közismert, nevezetes elemi geometriai feladatot és tételt egyfajta csemegeként. Legtöbb esetben az állítás kimondása után csak szakirodalmi referenciát adunk.

13.1. feladat (Izogonális pont, Fermat-Toricelli pont).
Adott  hegyesszögű háromszögben keressük meg azt pontot, aminek a csúcsoktól mért távolságösszege minimális! Mutassuk meg, hogy ez a pont egyértelmű, belőle minden oldal ugyanakkora szög alatt látszik!

A feladatra több megoldás is ismert, ezeket gyűjtötte össze Szmerka Gergely 2008. áprilisi KöMaL-cikkében.

A Fermat-Torricelli pontról bővebben az alábbi prezentációban olvashatunk.

13.2. feladat (Fagnano feladata, talpponti háromszög).
Adott a hegyesszögű  háromszög, egy $H$ háromszöget az -ba írtnak mondunk, ha  egy-egy csúcsa illeszkedik  egy-egy oldalára. Tekintsük az  háromszög magasságvonalainak talppontjai által meghatározott háromszöget. Mutassuk meg, hogy az -be írt háromszögek közül a talpponti háromszög kerülete a legkisebb!

A feladat megoldása megtalálható például itt.

Szintén a talpponti háromszög fenti tulajdonságával foglalkozik H. S. M. Coxeter - S. L. Greitzer: Az újra felfedezett geometria c. könyvének 4.5. szakasza.

30. tétel (Euler-féle formula és a sugáregyenlotlenség).
Legyen egy (hegyesszögű) háromszög beírt körének sugara , körülírt körének sugara , a beírt és körülírt körök középpontjainak távolsága . Ekkor

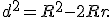1.  (Euler-féle formula)
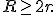2.  (sugáregyenlőtlenség)

Természetesen a sugáregyenlőtlenség azonnal következik az Euler-féle formulából, hiszen .

Az Euler-féle formula elemi bizonyítása megtalálható a Wikipédián.

Inverziót is használó bizonyítás, illetve némi kitekintés a témában található ebben a prezentációban.

31. tétel (Ptolemaiosz-tétel, Ptolemaiosz-egyenlotlenség).
Egy konvex négyszög oldalai a körüljárás szerint , ,  és , átlói  és . Ekkor 
egyenlőség pontosan húrnégyszögekre teljesül.

A Ptolemaiosz-tételt sokszor csak egyenlőség formájában mondják ki húrnégyszögekre. A vonatkozó Wikipédia szócikk is ezt a formát bizonyítja. Az általános egyenlőtlenség bizonyítása megtalálható pl. Reimann István: Nemzetközi matematikai olimpiák (1959-2003) c. könyv 7. fejezetének [24] szakaszában.

32. tétel (Erdos-Mordell egyenlotlenség)).
Legyen  az  belső vagy határpontja, az oldalegyenesktől mért távolságai rendre  és , míg a csúcsoktól mért távolságai  és . Ekkor

és egyenlőség csak akkor teljesül, ha  az  szabályos háromszög középpontja.

Az Erdős-Mordell egyenlőtlenség az elemi háromszöggeometria egyik legmélyebb eredménye. Sok szép következménye ismert, például a korábban látott sugáregyenlőtlenség is következik belőle. Számtalan kapcsolódó szakirodalom létezik, ezek közül mi melegen ajánljuk Kubatov Antal vonatkozó cikkét.(Pdf formátumban elérhető itt.) Szintén olvashatunk az Erdős-Mordell tételről Reimann István: Nemzetközi matematikai olimpiák (1959-2003) c. könyv 7. fejezetében.