9.2. Euklidészi alapszerkesztések
9.1. gyakorlat. Szerkesszük meg egy adott ![]() szakasz szakaszfelező merőlegesét!
szakasz szakaszfelező merőlegesét!
Megoldás.Ismétlésül idézzük fel a szakaszfelező merőleges fogalmát: azon pontok halmaza a síkon, amelyek a szakasz két végpontjától egyenlő távolságra vannak. Tudjuk, hogy a keresett alakzat egy egyenes, ezért elég lenne két pontját megszerkeszteni. Ilyeneket viszont könnyen találunk, ha ![]() és
és ![]() körül is rajzolunk egy-egy
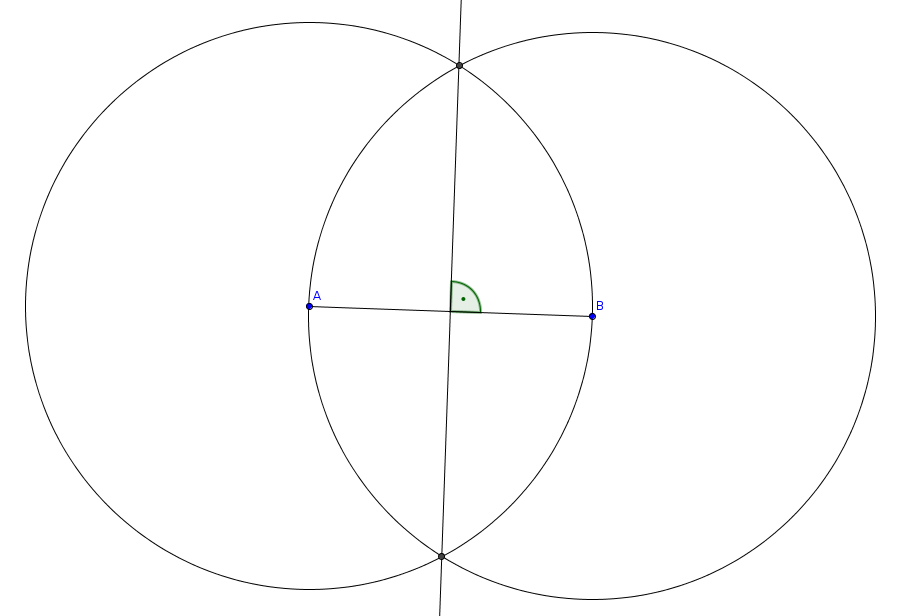
körül is rajzolunk egy-egy ![]() sugarú kört, akkor ezek metszéspontjai nyilvánvalóan rajta lesznek a keresett szakaszfelező merőlegesen. Ezek alapján a szerkesztés részletes menete (lásd 21. ábra):
sugarú kört, akkor ezek metszéspontjai nyilvánvalóan rajta lesznek a keresett szakaszfelező merőlegesen. Ezek alapján a szerkesztés részletes menete (lásd 21. ábra):
- szúrjuk
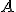 -ba a körzőt, nyissuk ki
-ba a körzőt, nyissuk ki 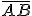 nyílásra, és rajzoljuk meg az
nyílásra, és rajzoljuk meg az 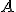 körüli
körüli 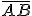 sugarú kört;
sugarú kört; - hasonlóan rajzoljuk meg a
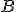 körüli
körüli 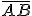 sugarú kört;
sugarú kört; - a két kör metszéspontjait összekötő egyenes a keresett szakaszfelező merőleges.
Elemzés: a feladatnak mindig pontosan egy megoldása van.![]()
9.2. gyakorlat. Adott az ![]() egyenes és egy
egyenes és egy ![]() pont. Szerkesszük meg azt az
pont. Szerkesszük meg azt az ![]() -re merőleges egyenest, ami illeszkedik
-re merőleges egyenest, ami illeszkedik ![]() -re!
-re!
Megoldás.Visszavezetjük a feladatot előzőre. Elég lenne kijelölnünk egy olyan szakaszt ![]() -n, aminek a szakaszfelező merőlegese átmegy
-n, aminek a szakaszfelező merőlegese átmegy ![]() -n. Ez utóbbi pontosan akkor teljesül, ha
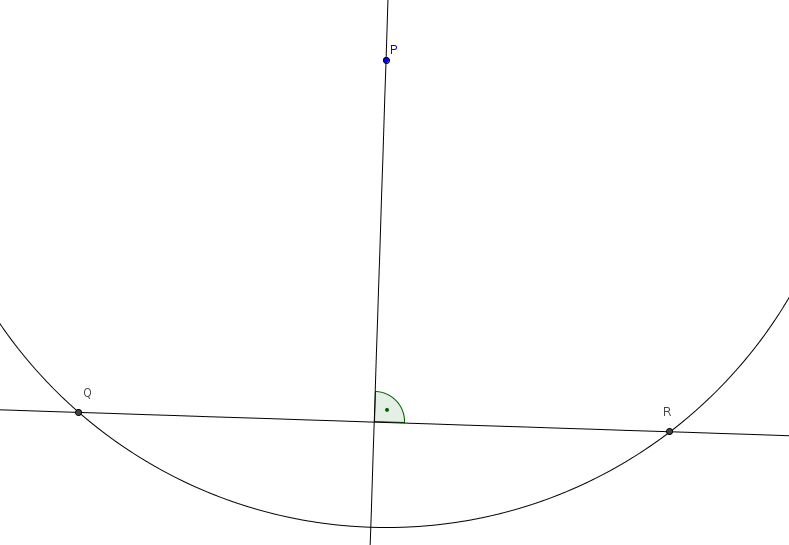
-n. Ez utóbbi pontosan akkor teljesül, ha ![]() a szakasz végpontjaitól egyenlő távolságra van. Ezek alapján a szerkesztés menete (22. ábra):
a szakasz végpontjaitól egyenlő távolságra van. Ezek alapján a szerkesztés menete (22. ábra):
- jelöljünk meg
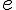 -n egy (
-n egy (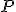 -től különböző és távoli) tetszőleges
-től különböző és távoli) tetszőleges 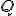 pontot;
pontot; - rajzoljunk
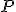 körül
körül 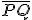 sugarú kört;
sugarú kört; - legyen a kör és
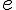 egyenes
egyenes 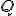 -n kívüli második metszéspontja
-n kívüli második metszéspontja 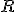 ;
; - szerkesszünk meg
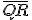 szakaszfelező merőlegesét, ez illeszkedik
szakaszfelező merőlegesét, ez illeszkedik 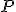 -re, és merőleges
-re, és merőleges 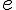 -re.
-re.
Elemzés: a feladatnak mindig pontosan egy megoldása van.
Megjegyzés: előfordulhat, hogy a rajzolt segédkör csak ![]() -ban metszi
-ban metszi ![]() -t, ilyenkor éppen
-t, ilyenkor éppen ![]() a keresett egyenes. A szerkesztési feladatok megoldásánál általában feltesszük, hogy a választott pont nem speciális. (Ez egyébként jogos feltevés, hiszen ha véletlenül speciális pontot válaszottunk, újrakezdjük az eljárást új segédpontot használva. Illetve kimutatható, hogy a nem speciális segédpont is szerkeszthető, de ennek részletezése csak körülményessé tenné a leírást, és gyakorlati jelentősége igazából nincs.)
a keresett egyenes. A szerkesztési feladatok megoldásánál általában feltesszük, hogy a választott pont nem speciális. (Ez egyébként jogos feltevés, hiszen ha véletlenül speciális pontot válaszottunk, újrakezdjük az eljárást új segédpontot használva. Illetve kimutatható, hogy a nem speciális segédpont is szerkeszthető, de ennek részletezése csak körülményessé tenné a leírást, és gyakorlati jelentősége igazából nincs.) ![]()
9.3. gyakorlat. Adott az ![]() egyenes és egy
egyenes és egy ![]() pont. Szerkesszük meg azt az
pont. Szerkesszük meg azt az ![]() -vel párhuzamos egyenest, ami illeszkedik
-vel párhuzamos egyenest, ami illeszkedik ![]() -re!
-re!
I. megoldás. Kétszer alkalmazva az előzőeket célba érhetünk. Először szerkesszünk egy tetszőleges ![]() egyenest, ami merőleges
egyenest, ami merőleges ![]() -re. Majd szerkesszünk
-re. Majd szerkesszünk ![]() -re illeszkedő,
-re illeszkedő, ![]() -re merőleges egyenest, ez megoldása a feladatunknak.
-re merőleges egyenest, ez megoldása a feladatunknak.![]()
II. megoldás. Az I. megoldásban adott módszer szükségtelenül hosszadalmas - kihasználva a paralelogrammáról tanultakat, gyorsabban célba érhetünk. Ha sikerül egy olyan paralelogrammát szerkeszteni, aminek egyik csúcsa ![]() , és egy
, és egy ![]() -re nem illeszkedő oldalegyenese
-re nem illeszkedő oldalegyenese ![]() , akkor készen vagyunk. A szerkesztés menete (23. ábra):
, akkor készen vagyunk. A szerkesztés menete (23. ábra):
- jelöljünk meg
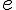 -n két tetszőleges
-n két tetszőleges 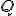 és
és 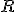 pontokat;
pontokat; - rajzoljunk
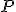 körül
körül 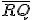 sugarú kört;
sugarú kört; - rajzoljunk
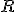 körül
körül 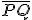 sugarú kört;
sugarú kört; - a két kör
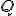 -n kívüli második metszéspontja legyen
-n kívüli második metszéspontja legyen 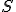 ,
, 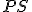 egyenes megfelelő.
egyenes megfelelő.
Elemzés: a két kör két pontban metszi egymást, de az egyik metszéspont hamis megoldást ad, feladatnak mindig pontosan egy megoldása van.![]()
9.4. gyakorlat. Szerkesszünk háromszöget, ha adott három oldalának hossza.
Megoldás.Keressük ![]() háromszöget, ha adottak
háromszöget, ha adottak ![]() és
és ![]() oldalai. Jelöljük ki
oldalai. Jelöljük ki ![]() és
és ![]() csúcsokat egymástól
csúcsokat egymástól ![]() távolságra egymástól. Az
távolságra egymástól. Az ![]() csúcs
csúcs ![]() -től
-től ![]() ,
, ![]() -től
-től ![]() távolságra van, így előállítható két kör metszéspontjaként. A szerkesztés menete:
távolságra van, így előállítható két kör metszéspontjaként. A szerkesztés menete:
- a tetszőleges
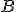 pont körül szerkesszünk
pont körül szerkesszünk 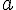 sugárral kört, majd a körvonalon jelöljünk ki tetszőleges
sugárral kört, majd a körvonalon jelöljünk ki tetszőleges 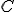 pontot;
pontot; - rajzoljunk
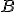 körül
körül 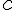 sugarú kört;
sugarú kört; - rajzoljunk
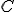 körül
körül 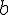 sugarú kört;
sugarú kört; - a két kör második metszéspontjai szolgáltatják a keresett
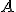 csúcsokat .
csúcsokat .
Elemezés: ![]() pont helyzete és a
pont helyzete és a ![]() oldalegyenes tetszés szerint kijelölhető. Ezután a szerkesztés két különböző
oldalegyenes tetszés szerint kijelölhető. Ezután a szerkesztés két különböző ![]() csúcsot, és mindegyikhez két különböző
csúcsot, és mindegyikhez két különböző ![]() csúcsot szolgáltathat.
csúcsot szolgáltathat. ![]() csúcs mindig szerkeszthető, vegyük azonban észre, hogy
csúcs mindig szerkeszthető, vegyük azonban észre, hogy ![]() -t adó körök nem feltétlen metszik egymást. Könnyű meggondolni, hogy a metszés feltétele, hogy a háromszög oldalaira az
-t adó körök nem feltétlen metszik egymást. Könnyű meggondolni, hogy a metszés feltétele, hogy a háromszög oldalaira az ![]() ,
, ![]() és $c<a+b$ háromszög-egyenlőtlenségek egyszerre teljesüljenek. Világos azonban, hogy ha létezik megoldás, akkor a háromszögek egybevágóságának alapesetei miatt az összes kapott megoldás egybevágó, ezek között nem szokás különbséget tenni: a feladatnak pontosan egy megoldása van, ha az adatok kielégítik az
és $c<a+b$ háromszög-egyenlőtlenségek egyszerre teljesüljenek. Világos azonban, hogy ha létezik megoldás, akkor a háromszögek egybevágóságának alapesetei miatt az összes kapott megoldás egybevágó, ezek között nem szokás különbséget tenni: a feladatnak pontosan egy megoldása van, ha az adatok kielégítik az ![]() ,
, ![]() és
és ![]() háromszög-egyenlőtlenségeket. Ha valamelyik esetben szigorú egyenlőtlenség helyett egyenlőség teljesül, akkor elfajuló megoldásként három kollineáris pontot kapunk, ezt mi nem tekintjük háromszögnek.
háromszög-egyenlőtlenségeket. Ha valamelyik esetben szigorú egyenlőtlenség helyett egyenlőség teljesül, akkor elfajuló megoldásként három kollineáris pontot kapunk, ezt mi nem tekintjük háromszögnek.![]()
9.5. gyakorlat. Adott egy ![]() nagyságú szög, egy
nagyságú szög, egy ![]() pont, és egy
pont, és egy ![]() kezdőpont
kezdőpont ![]() félegyenes. Szerkesszünk
félegyenes. Szerkesszünk ![]() kezdőpontú
kezdőpontú ![]() félegyenest úgy, hogy
félegyenest úgy, hogy ![]() és
és ![]() által bezárt szög az adott
által bezárt szög az adott ![]() szöggel egyenlő legyen.
szöggel egyenlő legyen.
Megoldás. Válasszunk az adott ![]() nagyságú stög szárain tetszőleges
nagyságú stög szárain tetszőleges ![]() és
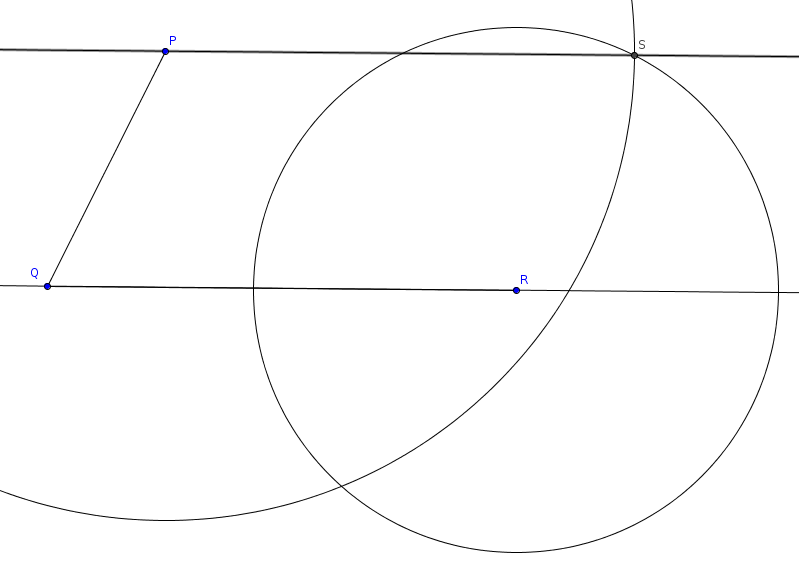
és ![]() pontokat, csúcsát jelölje $R$. A
pontokat, csúcsát jelölje $R$. A ![]()
![]() szöge éppen
szöge éppen ![]() . Az előbbiek szerint tudunk
. Az előbbiek szerint tudunk ![]() -lel egybevágó háromszöget szerkeszteni, amelynek egyik csúcsa
-lel egybevágó háromszöget szerkeszteni, amelynek egyik csúcsa ![]() , erre illeszkedő oldalegyenese $e$, és
, erre illeszkedő oldalegyenese $e$, és ![]() -nál
-nál ![]() szöge van. A részleteket az olvasóra bízzuk.
szöge van. A részleteket az olvasóra bízzuk.![]()
9.6. gyakorlat. Szerkesszük meg egy adott szög (belső) szögfelezőjét.
Mielőtt a feladat megoldását megismerjük, ismételjük át a rombuszról tanultakat!
Megoldás. A szögfelező értelemszerűen illeszkedik a szög csúcsára, így elég lenne még egy pontját megkeresni. Segítségül hívjuk a rombuszról tanultakat: a rombusz átlói felezik a belső szögeit. Ezek alapján a szerkesztés menete (24. ábra):
- legyen az adott szög csúcsa
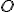 , és jelöljünk ki egy tetszőleges
, és jelöljünk ki egy tetszőleges 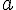 hosszúságú szakaszt;
hosszúságú szakaszt; - szerkesszünk
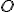 körül
körül 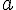 sugarú kört, ez messe a szögszárakat
sugarú kört, ez messe a szögszárakat 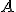 -ban és
-ban és 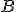 -ben;
-ben; - szerkesszünk
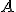 körüli
körüli 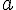 sugarú, és
sugarú, és 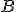 körüli
körüli 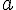 sugarú kört;
sugarú kört; - a két kör
 -tól különböző, második metszéspontja illeszkedik a keresett szögfelezőre.
-tól különböző, második metszéspontja illeszkedik a keresett szögfelezőre.
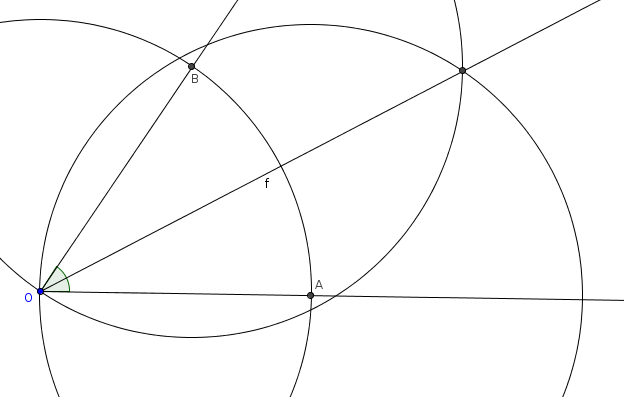
Elemzés: pontosan egy megoldás van.![]()